- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Тригонометрические функции числового аргумента
Содержание
- 1. Презентация Тригонометрические функции числового аргумента
- 2. Рассмотреть связь между радианной и градусной мерами
- 3. числовая окружность,синус, косинус, тангенс и котангенс числового
- 4. Укажите соответствие:тупой уголпрямой уголразвёрнутый угол полный уголострый угол
- 5. Угол поворотахОР0 - неподвижный лучОР - подвижный
- 6. Радианная мера углауОРх1 радиан это центральный угол,
- 7. Заполните таблицууОх90°270°180°0°360° интервал в градусахчетвертьIIIIVIII
- 8. Синусом угла α называется ордината точки, полученной
- 9. № 407, 408, 416 – 418, 420,
Рассмотреть связь между радианной и градусной мерами угла;Закрепить умения выполнять переход от радианной меры угла к градусной мере и наоборот.Ввести понятие тригонометрической функции числового аргументаЦели и задачи
Слайд 2Рассмотреть связь между радианной и градусной мерами угла;
Закрепить умения выполнять переход
от радианной меры угла к градусной мере и наоборот.
Ввести понятие тригонометрической функции числового аргумента
Ввести понятие тригонометрической функции числового аргумента
Цели и задачи
Слайд 3числовая окружность,
синус, косинус, тангенс и котангенс числового аргумента;
радиан, радианная мера угла;
основные
тождества;
соотношения между градусной и радианной мерами угла.
соотношения между градусной и радианной мерами угла.
Основные понятия
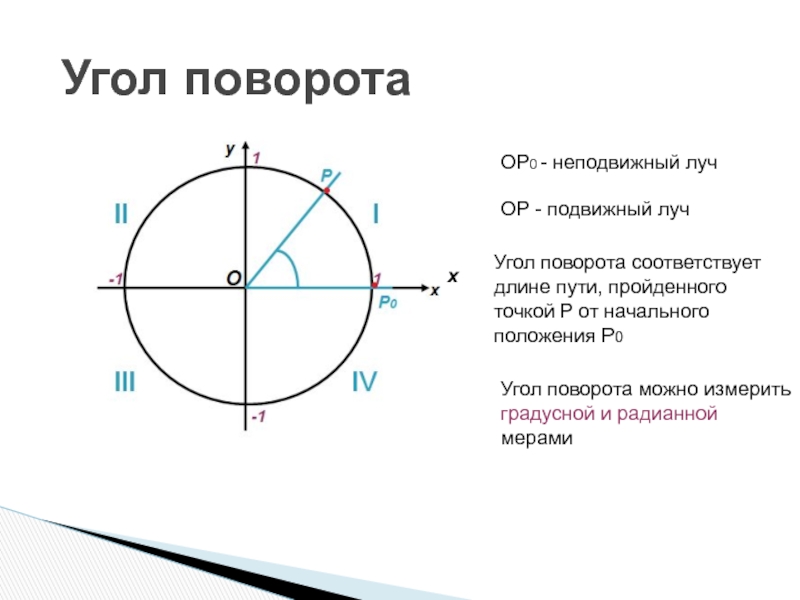
Слайд 5Угол поворота
х
ОР0 - неподвижный луч
ОР - подвижный луч
Угол поворота соответствует длине
пути, пройденного точкой Р от начального положения Р0
Угол поворота можно измерить градусной и радианной мерами
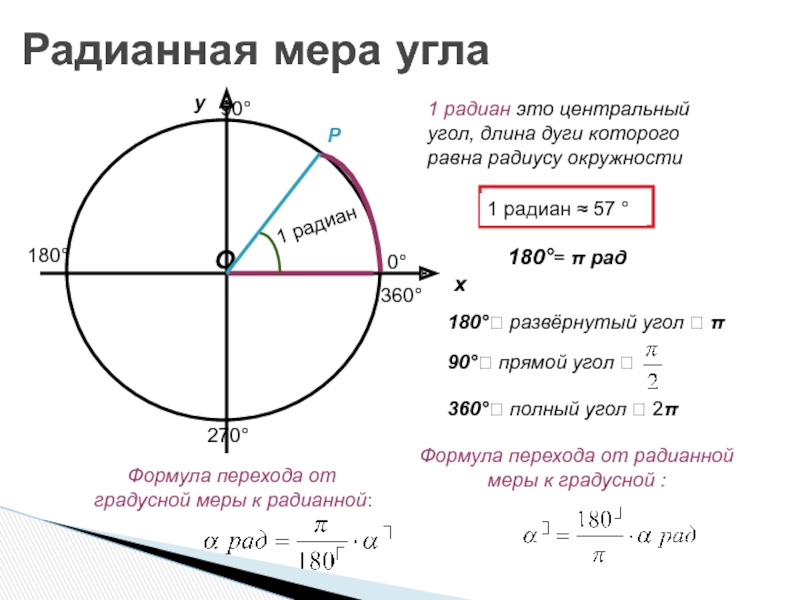
Слайд 6Радианная мера угла
у
О
Р
х
1 радиан это центральный угол, длина дуги которого равна
радиусу окружности
1 радиан
1 радиан 57 °
90°
270°
180°
0°
360°
180°= рад
180° развёрнутый угол
90° прямой угол
360° полный угол 2
Формула перехода от радианной меры к градусной :
Формула перехода от градусной меры к радианной:
Слайд 7Заполните таблицу
у
О
х
90°
270°
180°
0°
360°
интервал в градусах
четверть
I
II
IV
III
Определите, в какой четверти расположены углы:
= 40°
= -110°
= 460°
= -220°
интервал в радианах
Слайд 8Синусом угла α называется ордината точки, полученной поворотом точки (1; 0)
вокруг начала координат на угол α (обозначается
sin α)
Косинусом угла α называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (обозначается cos α)
Тангенсом угла α называется отношение синуса угла α к его косинусу (обозначается tg α)
Косинусом угла α называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (обозначается cos α)
Тангенсом угла α называется отношение синуса угла α к его косинусу (обозначается tg α)
Определения
Слайд 9№ 407, 408, 416 – 418, 420, 429, 442.
Алимов Ш.А. Алгебра
и начала математического анализа. 10–11 кл.
Закрепление изученного
Домашнее задание
№ 414, 424, 443.
