алгебра 7 класс
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад : Сумма и разность кубов
Содержание
- 1. Презентация : Сумма и разность кубов
- 2. вывести формулы
- 3. Устный счетРазложить многочлен на множители:8x –12y a4
- 4. Устно:Представить в виде куба: 8х3 64с6 b12
- 5. Устно:Представить в виде куба: 27х3 =
- 6. Устно:Представить в виде куба:
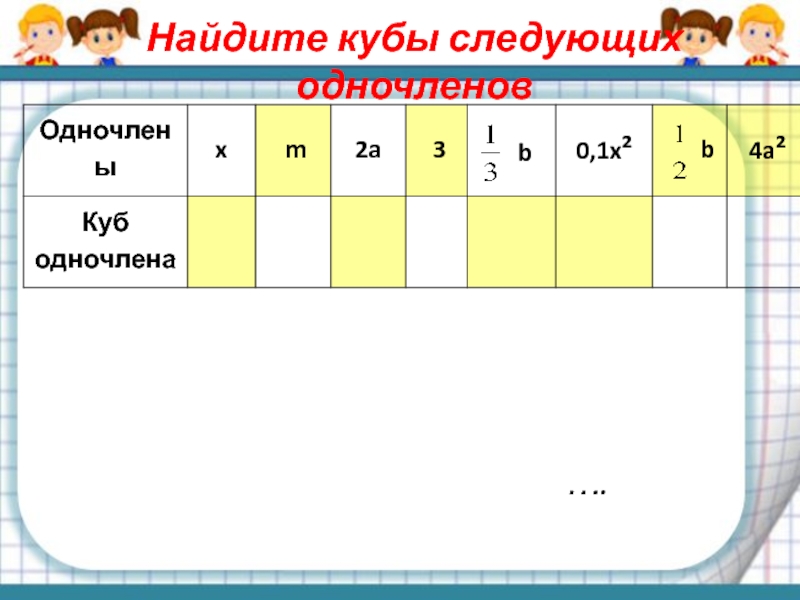
- 7. Найдите кубы следующих одночленов….
- 8. Проверь себяКритерий оценки:
- 9. Формула суммы кубовСумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
- 10. Для разложения на множители суммы кубов используют тождество- формула суммы кубовДокажем ее.
- 11. Слайд 11
- 12. Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат разности
- 13. Алгоритм разложения cуммы кубов на множители:1.Представить двучлен
- 14. Формула разности кубовРазность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
- 15. Для разложения на множители разности кубов используют тождество- формула разности кубовДокажем ее.
- 16. Слайд 16
- 17. Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат суммы.
- 18. Алгоритм разложения разности кубов на множители:1.Представить двучлен
- 19. a³ + b³ = (a + b)
- 20. Разложите на множители
- 21. Разложите на множители:
- 22. Разложите на множители:
- 23. …. 27 + b³ = 3
- 24. Смотри не ошибись!I вариантx2- 81m2-20m +10025x2+40x+16
- 25. Проверка I вариант(x
- 26. Итоги урока:– Назовите формулы суммы и разности
- 27. Спасибо за урок !
вывести формулы суммы и разности кубов; сформировать умение применять их при разложении многочлена на множителиЦели урока :
Слайд 2 вывести формулы суммы и разности кубов; сформировать умение применять
их при разложении многочлена на множители
Цели урока :
Слайд 3Устный счет
Разложить многочлен на множители:
8x –12y
a4 + a2b
x3- 3x2-
3x
9p4+ 36p2- 27p
Представить в виде квадрата двучлена:
a2- 2ab + b2
a2- 12ab +36
81- 18y + y2
9p4+ 36p2- 27p
Представить в виде квадрата двучлена:
a2- 2ab + b2
a2- 12ab +36
81- 18y + y2
= 4(2x -3у)
= a2(a2+b)
= x(x2- 3x -1)
= 9p (p3+4p -3)
= (a –b)2
= (a – 6)
= (9 + y)2
Слайд 9Формула суммы кубов
Сумма кубов двух выражений равна произведению суммы этих выражений
и неполного квадрата их разности.
Слайд 10Для разложения на множители суммы кубов используют тождество
- формула суммы кубов
Докажем
ее.
Слайд 12Сумма кубов двух выражений равна произведению суммы этих выражений на неполный
квадрат разности
Слайд 13Алгоритм разложения cуммы кубов на множители:
1.Представить двучлен в виде суммы кубов.
2.Выполнить
разложение по формуле а3+в3= (а + в)(а2 - aв + b2) сумма кубов
Пример:
27 + m3= (3)3+ m3=(3 + m) ((3)2 – 3*m+ m2) = (3 + m)(9- 3m +m2)
Пример:
27 + m3= (3)3+ m3=(3 + m) ((3)2 – 3*m+ m2) = (3 + m)(9- 3m +m2)
Слайд 14Формула разности кубов
Разность кубов двух выражений равна произведению разности этих выражений
и неполного квадрата их суммы.
Слайд 15Для разложения на множители разности кубов используют тождество
- формула разности кубов
Докажем
ее.
Слайд 17Разность кубов двух выражений равна произведению разности этих выражений на неполный
квадрат суммы.
Слайд 18Алгоритм разложения разности кубов на множители:
1.Представить двучлен в виде разности кубов.
2.Выполнить
разложение по формуле
а3-в3= (а- в)(а2+ aв + b2) разность кубов
Пример:
64а6- 8b9=(4a2)3 - (2b3)3 =(4a2 – 2b3)((4a2)2+ 4a2*2b3 +(2b3)2)=(4a2- 2b3)(16a4+ 8a2b3+4b6 )
а3-в3= (а- в)(а2+ aв + b2) разность кубов
Пример:
64а6- 8b9=(4a2)3 - (2b3)3 =(4a2 – 2b3)((4a2)2+ 4a2*2b3 +(2b3)2)=(4a2- 2b3)(16a4+ 8a2b3+4b6 )
Слайд 19a³ + b³ = (a + b) (a² - ab +
b²)
Сумма
кубов
Сумма
кубов
Сумма
выражений
Неполный квадрат
их разности
Формулы:
a³ - b³ = (a - b) (a² + ab + b²)
Разность
кубов
Разность
выражений
Неполный квадрат
их суммы
Слайд 23….
27 + b³ = 3 ³ + b³ =
(3 + b)(3² - 3b + b²)
a³ - 8c³ = a³ - (2с)³ = (a – 2с)(a² + 2aс + (2с )²)
Слайд 24Смотри не ошибись!
I вариант
x2- 81
m2-20m +100
25x2+40x+16
64a3- 27d3
II вариант
x2- 25
x2-16x +64
49x2+56x+16
8a3+ 216d3
Слайд 25Проверка
I вариант
(x -9)(x+9)
(m-10)2
(5x +4)2
(4a – 3d)(16a2+
12ad +9d2)
II вариант
(x-5)(x+5)
(x -8)2
(7x +4)2
(2a + 6d)(4a2-12ad +36d2)
II вариант
(x-5)(x+5)
(x -8)2
(7x +4)2
(2a + 6d)(4a2-12ad +36d2)
Слайд 26Итоги урока:
– Назовите формулы суммы и разности кубов.
– Когда применяются эти
формулы?
– Какие ещё формулы позволяют разложить многочлен на множители? Назовите их.
– Какие ещё формулы позволяют разложить многочлен на множители? Назовите их.
