- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Способы решения квадратных уравнений
Содержание
- 1. Презентация Способы решения квадратных уравнений
- 2. Квадратные уравнения
- 3. 1. Разложение левой части уравнения на
- 4. 2. Метод выделения полного квадратаРешим уравнение х2
- 5. 3. Решение квадратных уравнений по формуле
- 6. Формула (1) корней квадратного уравнения
- 7. 4. Решение уравнений с использованием теоремы Виета
- 8. 5. Решение уравнений способом «переброски!»ах = у
- 9. 6. Свойства коэффициентов
- 10. 2. Если а - b +
- 11. Б. Если второй коэффициент - четное число,
- 12. В. Приведенное уравнение
- 13. Для запоминания формулы для решения приведенного квадратного
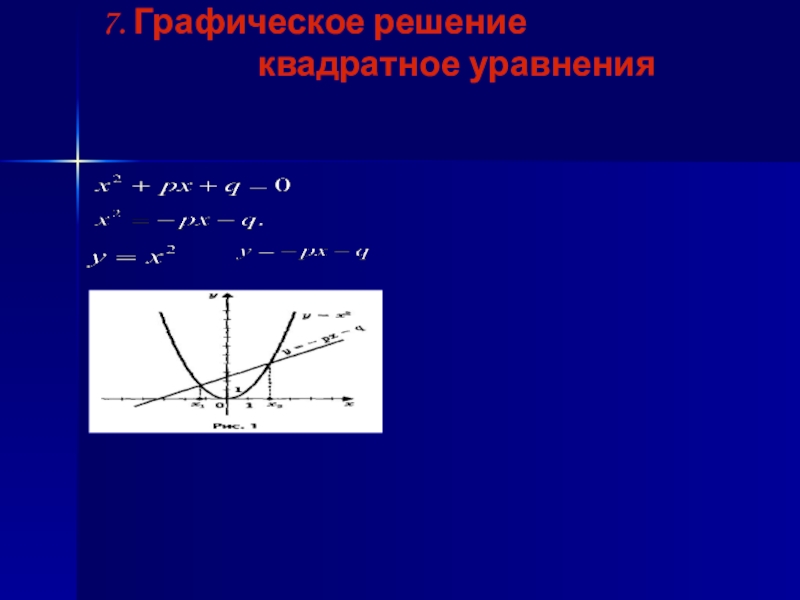
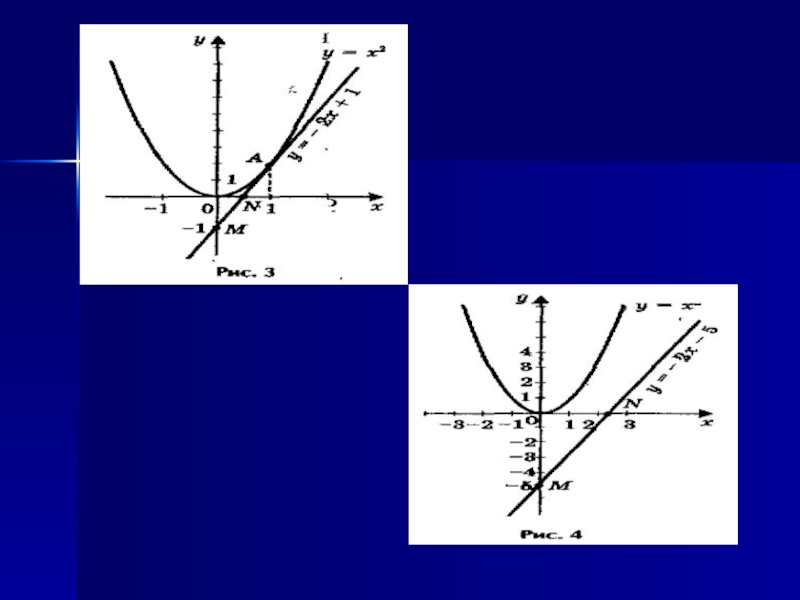
- 14. 7. Графическое решение
- 15. Слайд 15
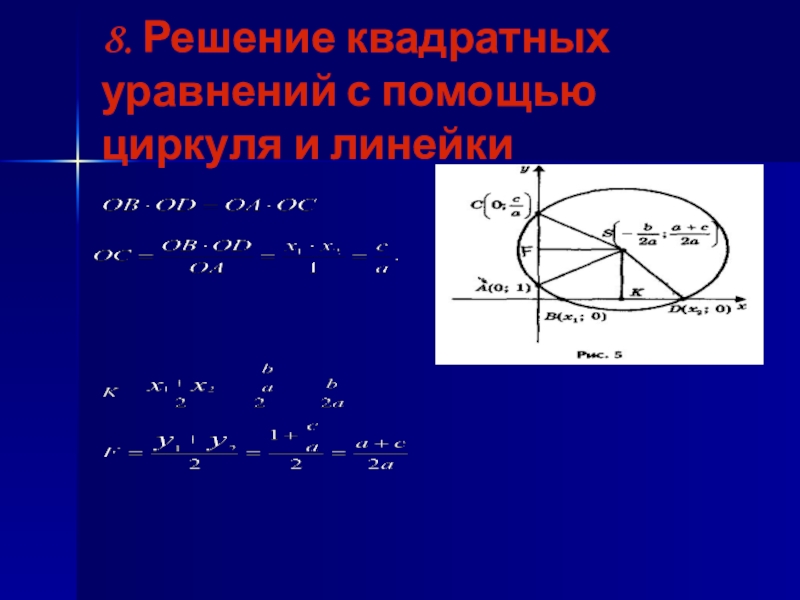
- 16. 8. Решение квадратных уравнений с помощью циркуля и линейки
- 17. а)
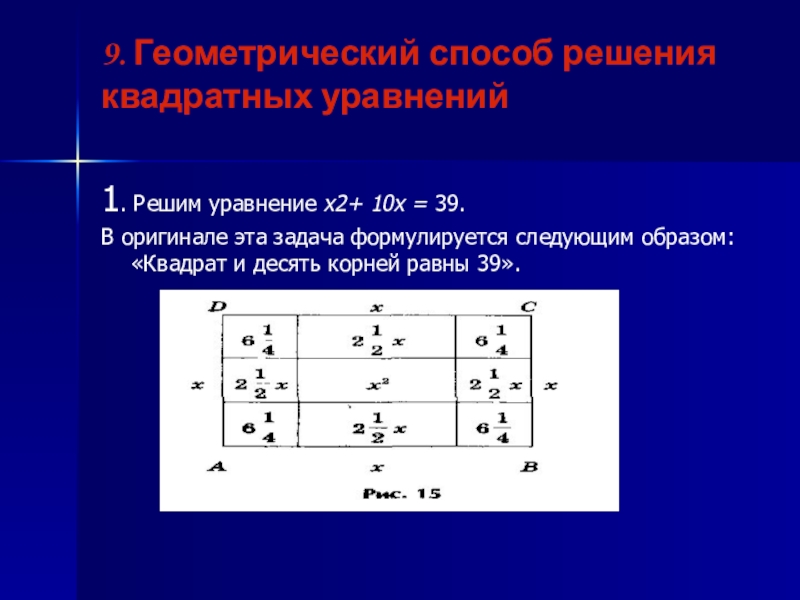
- 18. 9. Геометрический способ решения квадратных уравнений1. Решим
- 19. Слайд 19
- 20. Спасибо.
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. В
Слайд 2 Квадратные уравнения - это фундамент, на
котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Рассмотрим девять способов решения квадратных уравнений. Подробно разберем каждый из них.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Рассмотрим девять способов решения квадратных уравнений. Подробно разберем каждый из них.
Слайд 31. Разложение левой части
уравнения на
множители
1. Решим уравнение х2
+ 10х - 24 = 0,
х2 + 10х - 24 = х2 + 12х – 2х - 24 =
= х(х + 12) - 2(х+ 12) = (х + 12)(х - 2).
(х + 12)(х - 2) = 0.
х = 2, х =- 12.
числа 2 и - 12 являются корнями уравнения
х2 + 10х - 24 =0.
2.
х2 + 3х + 2 = О,
(х2 + 2х) + (х + 2) = О,
х(х + 2) + (х + 2) = О, (х + 1)(х + 2) = О, х + 1 = 0 или х + 2 = О, х1 = - 1 или х2 = - 2.
Уравнение х2 + 3х + 2 = О имеет два корня: х1 = - 1, х2 = - 2.
х2 + 10х - 24 = х2 + 12х – 2х - 24 =
= х(х + 12) - 2(х+ 12) = (х + 12)(х - 2).
(х + 12)(х - 2) = 0.
х = 2, х =- 12.
числа 2 и - 12 являются корнями уравнения
х2 + 10х - 24 =0.
2.
х2 + 3х + 2 = О,
(х2 + 2х) + (х + 2) = О,
х(х + 2) + (х + 2) = О, (х + 1)(х + 2) = О, х + 1 = 0 или х + 2 = О, х1 = - 1 или х2 = - 2.
Уравнение х2 + 3х + 2 = О имеет два корня: х1 = - 1, х2 = - 2.
Слайд 42. Метод выделения полного квадрата
Решим уравнение х2 + 6х - 7
= 0.
х2 + 6х = х2 + 2х3.
х2 + 2-х-3 + 32 = (х + 3)2.
х2 + 6х - 7 = 0.,
х2 + 6х-7=х2 + 2.х 3 + 3 2 - 32 -7 =
=(х + 3)2 – 9– 7=(х + 3)2 - 16,
х + 3)2 – 16 =О,
т. е. (х + 3)2 = 16.
х + 3 = 4, х1 = 1,или х + 3 = - 4, х2 =-7
х2 + 6х = х2 + 2х3.
х2 + 2-х-3 + 32 = (х + 3)2.
х2 + 6х - 7 = 0.,
х2 + 6х-7=х2 + 2.х 3 + 3 2 - 32 -7 =
=(х + 3)2 – 9– 7=(х + 3)2 - 16,
х + 3)2 – 16 =О,
т. е. (х + 3)2 = 16.
х + 3 = 4, х1 = 1,или х + 3 = - 4, х2 =-7
Слайд 6 Формула (1) корней квадратного уравнения ах2 + bх +
с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный, из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
Слайд 96. Свойства коэффициентов
квадратного уравнения
А.
1.
Если (т. е, сумма
Коэффициентов уравнения равна нулю), то
х1 = 1, х2 = .
То х1 = 1, х2 = .
Слайд 10 2. Если а - b + с = 0, или
b = а + с, то
х1 = - 1,х2 =- ,
По условию а - b + с = 0, откуда b = а + с. Таким
образом,
т, е. х1 = - 1,х2 =- , что и требовалось доказать.
х1 = - 1,х2 =- ,
По условию а - b + с = 0, откуда b = а + с. Таким
образом,
т, е. х1 = - 1,х2 =- , что и требовалось доказать.
Слайд 13Для запоминания формулы для решения приведенного квадратного уравнения можно использовать такое
стихотворение:
р со знаком взяв обратным,
Мы на два его разделим.
И от корня аккуратно
Знаком «минус», «плюс» отделим.
А под корнем, очень кстати,
Половина р в квадрате,
Минус -
И вот решенье
Небольшого уравнения:
р со знаком взяв обратным,
Мы на два его разделим.
И от корня аккуратно
Знаком «минус», «плюс» отделим.
А под корнем, очень кстати,
Половина р в квадрате,
Минус -
И вот решенье
Небольшого уравнения:
Слайд 189. Геометрический способ решения квадратных уравнений
1. Решим уравнение х2+ 10х =
39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».