- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Способы решений квадратных уравнений
Содержание
- 1. Презентация Способы решений квадратных уравнений
- 2. Цель работыЦель нашей исследовательской работы – изучить
- 3. Что это такое?Квадратное уравнение — уравнение видаax2 + bx
- 4. ПрименениеБез квадратных уравнений не обойтись при различных
- 5. План работы:1. Разложение левой части уравнения на
- 6. Приступим!2x2 +6x=0x2 -18x+80=04x2 +12x+-55=0x²+2x-3=0x²-6x+8=02x²-11x+15=0x²+4x-5=0x²+10x=39Далее
- 7. Способ №1 Разложение левой части уравнения на
- 8. Способ №2 Метод выделения полного квадрата. С
- 9. Способ №3 Решение квадратных уравнений по формуле. Далее
- 10. ПродолжениеНачало
- 11. Способ №4 Графическое решение квадратного уравнения.Иногда квадратные
- 12. Способ №5 Решение уравнений с использованием теоремы Виета. Начало
- 13. Способ №6 Решение уравнений способом "переброски". Начало
- 14. Способ №7 Свойства коэффициентов квадратного уравнения. Начало
- 15. Способ №8 Геометрический способ решения квадратных уравнений. Начало
- 16. ВыводСуществует масса способов решения квадратных уравнений, и
- 17. Слайд 17
Цель работыЦель нашей исследовательской работы – изучить способы решения квадратных уравнений и выяснить, при каких обстоятельствах необходимо пользоваться тем или иным способом решения.
Слайд 2Цель работы
Цель нашей исследовательской работы – изучить способы решения квадратных уравнений
и выяснить, при каких обстоятельствах необходимо пользоваться тем или иным способом решения.
Слайд 3Что это такое?
Квадратное уравнение — уравнение вида
ax2 + bx + c = 0,
где a, b, c — некоторые числа
(a ≠ 0), x — неизвестное.
Числа называются коэффициентами квадратного уравнения.
a называется первым коэффициентом;
b называется вторым коэффициентом;
c — свободным членом.
(a ≠ 0), x — неизвестное.
Числа называются коэффициентами квадратного уравнения.
a называется первым коэффициентом;
b называется вторым коэффициентом;
c — свободным членом.
Слайд 4Применение
Без квадратных уравнений не обойтись при различных расчетах. Их можно использовать
при строительстве, чтобы выяснить траекторию движения планет, в самолетостроении. Важны арифметические расчеты и в спорте.
Слайд 5План работы:
1. Разложение левой части уравнения на множители
2. Метод выделения полного
квадрата
3. Решение квадратных уравнений по формуле
4. Графическое решение квадратного уравнения
5. Использование теоремы Виета
6. Решение уравнений способом «переброски»
7. Свойства коэффициентов квадратного уравнения
8. Геометрический способ и теорема Безу
9. Другие способы решения
3. Решение квадратных уравнений по формуле
4. Графическое решение квадратного уравнения
5. Использование теоремы Виета
6. Решение уравнений способом «переброски»
7. Свойства коэффициентов квадратного уравнения
8. Геометрический способ и теорема Безу
9. Другие способы решения
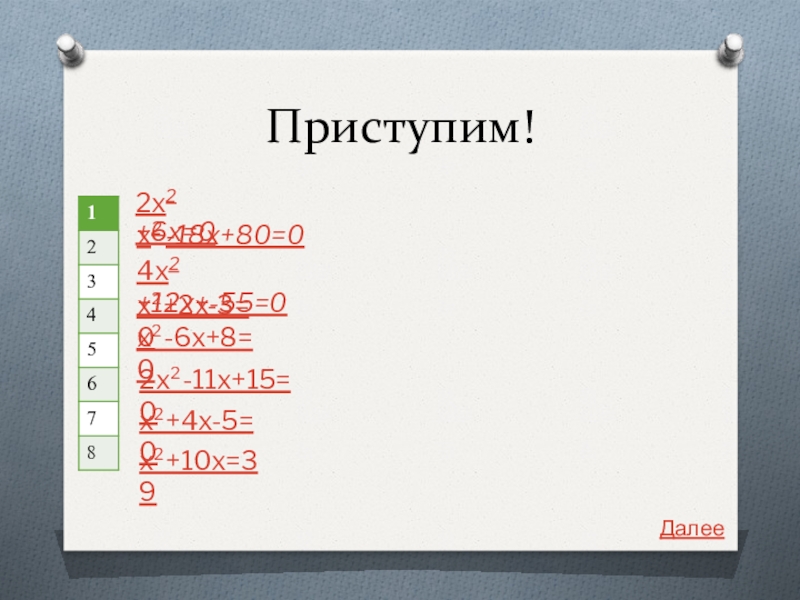
Слайд 6Приступим!
2x2 +6x=0
x2 -18x+80=0
4x2 +12x+-55=0
x²+2x-3=0
x²-6x+8=0
2x²-11x+15=0
x²+4x-5=0
x²+10x=39
Далее
Слайд 7Способ №1
Разложение левой части уравнения на множители.
Данным способом удобно решать неполные
квадратные уравнения.
2x2 +6x=0;
2x(x+3)=0;
2x=0; x+3=0;
X1=0; x2=-3;
Ответ:0;-3.
2x2 +6x=0;
2x(x+3)=0;
2x=0; x+3=0;
X1=0; x2=-3;
Ответ:0;-3.
Начало
Слайд 8Способ №2
Метод выделения полного квадрата.
С помощью этого способа мы приводим квадратное
уравнение к виду, при котором возможно воспользоваться формулами сокращённого умножения.
X2 -18x+80=0;
X2 -2*9x+81-81+80=0;
(x-9) 2 -1=0;
(x-9-1)(x-9+1)=0;
X-9-1=0; x-9+1=0;
X1=10; x2=8;
Ответ:10;8.
X2 -18x+80=0;
X2 -2*9x+81-81+80=0;
(x-9) 2 -1=0;
(x-9-1)(x-9+1)=0;
X-9-1=0; x-9+1=0;
X1=10; x2=8;
Ответ:10;8.
Начало
Слайд 11Способ №4
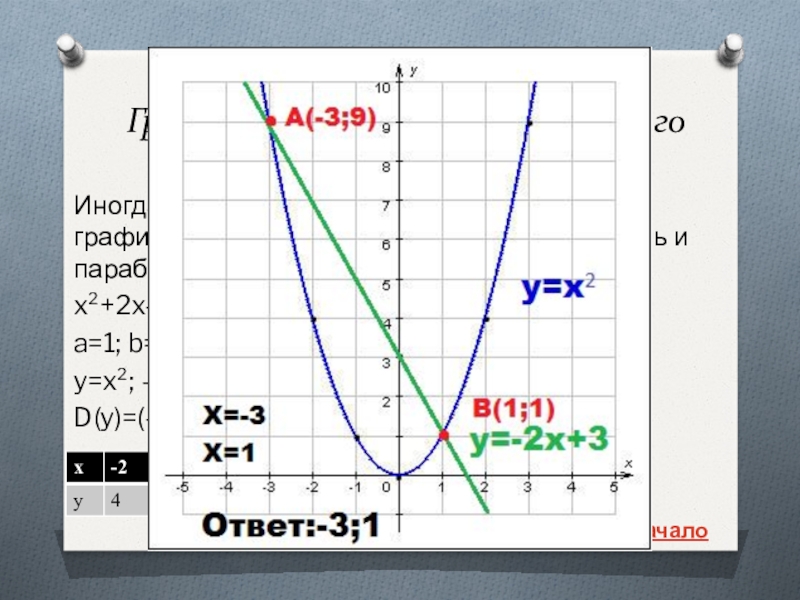
Графическое решение квадратного уравнения.
Иногда квадратные уравнения удобно решать графически, используя
координатную плоскость и параболу.
x²+2x-3=0;
a=1; b=2; c=-3;
y=x²; - парабола; y=-2x+3 – прямая;
D(y)=(-∞;+∞); D(y)=(-∞;+∞);
x²+2x-3=0;
a=1; b=2; c=-3;
y=x²; - парабола; y=-2x+3 – прямая;
D(y)=(-∞;+∞); D(y)=(-∞;+∞);
Начало
Слайд 16Вывод
Существует масса способов решения квадратных уравнений, и для каждого из них
возможно найти наиболее удобный и рациональный способ решения.