класса
МБОУ Алтайская СОШ №1
Научный руководитель :
Бабаева Галина Яковлевна
учитель математики
МБОУ Алтайская СОШ №1
с. Алтайское. Алтайского района
с. Алтайское. Алтайского района 2019 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Решение уравнений и неравенств графическим способом
Содержание
- 1. Презентация Решение уравнений и неравенств графическим способом
- 2. Цель моей работы : изложить графический метод
- 3. Актуальность темы: графический метод,
- 4. Алгоритм решения уравнений графическим способом.1. Составить функции
- 5. Графики основных функций: у = k x + b
- 6. Графическое решение линейных уравнений Задание :
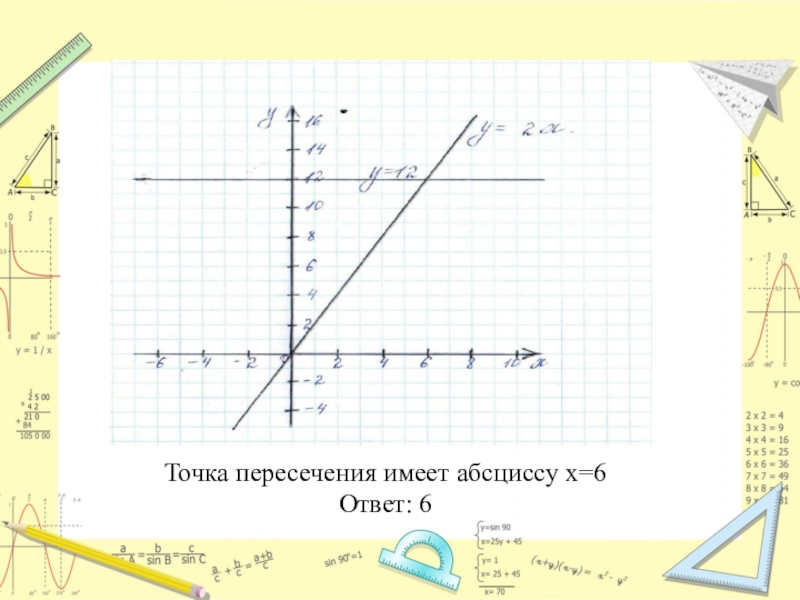
- 7. Точка пересечения имеет абсциссу x=6Ответ: 6
- 8. 2 способ решения: Построим графики функций: y=2x-10 и y=2.
- 9. Точка пересечения имеет абсциссу x=6Ответ: 6
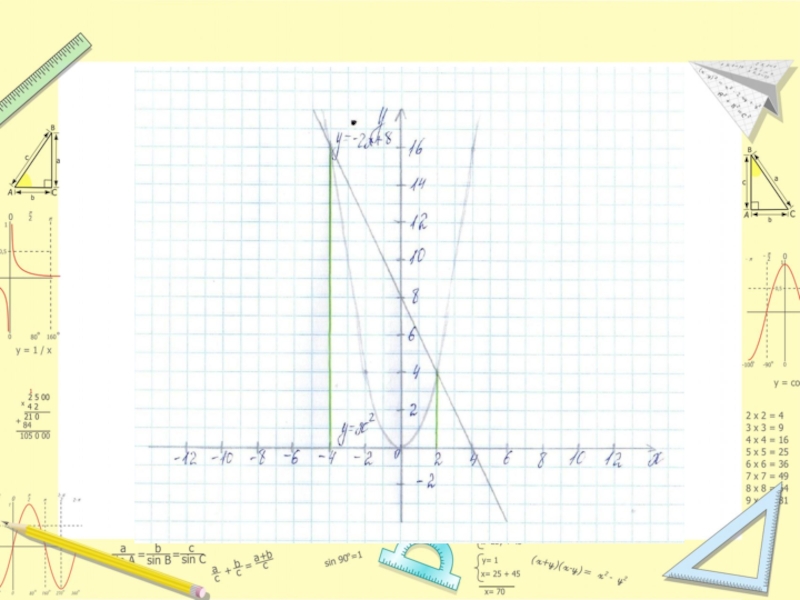
- 10. Решим графическим способом уравнение: x^2 +2x−8=01 способ:
- 11. Слайд 11
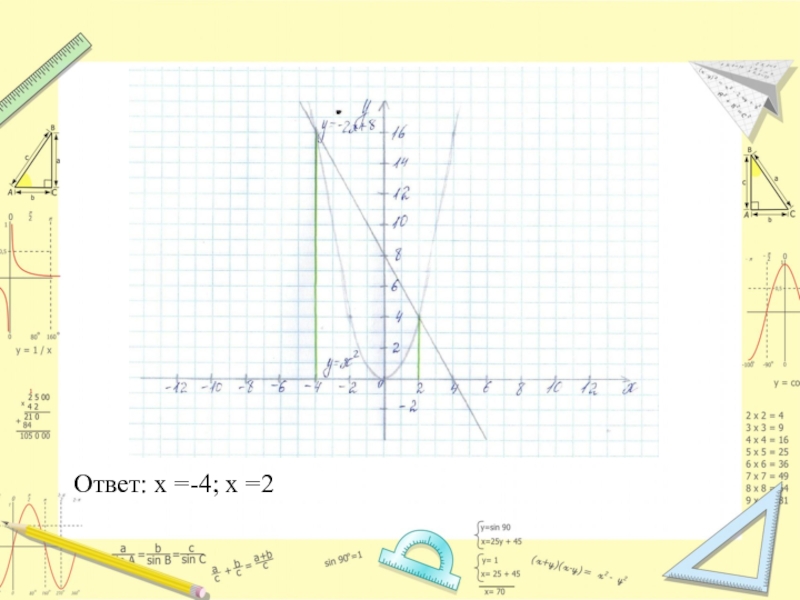
- 12. Ответ: x =-4; x =2
- 13. 2 способ: Перепишем уравнение в виде :x^2
- 14. Задание:Решить уравнение: x² - 2x=0Решение:Перепишем уравнение в виде: x² = 2x
- 15. Построим графики функций: y = x² и y = 2x: Ответ: х=0; х=2
- 16. Задание: Решим уравнение: х^ 2 +2=0Решение: Перепишем
- 17. Построим графики функций: у=-2 и у=
- 18. Задание:Решить графически уравнение: 3/х +2 = х
- 19. Строим графики функций : y = 3/х и y = х-2
- 20. Графики функций пересекаются в точках с координатами:
- 21. Задание: Решить уравнение : 2 х^3 –
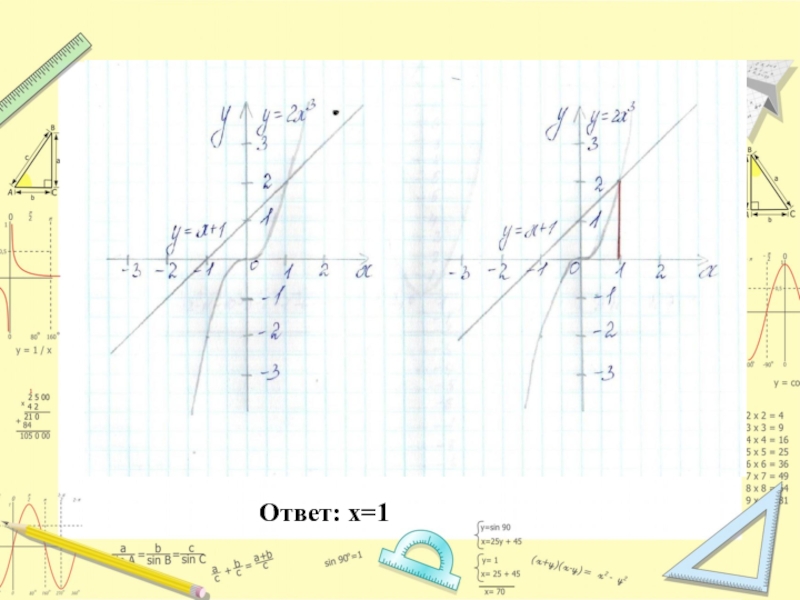
- 22. Ответ: х=1
- 23. Задание: Решить уравнение: √ x -
- 24. Графики функций пересекаются в двух
- 25. Алгоритм решения неравенств.
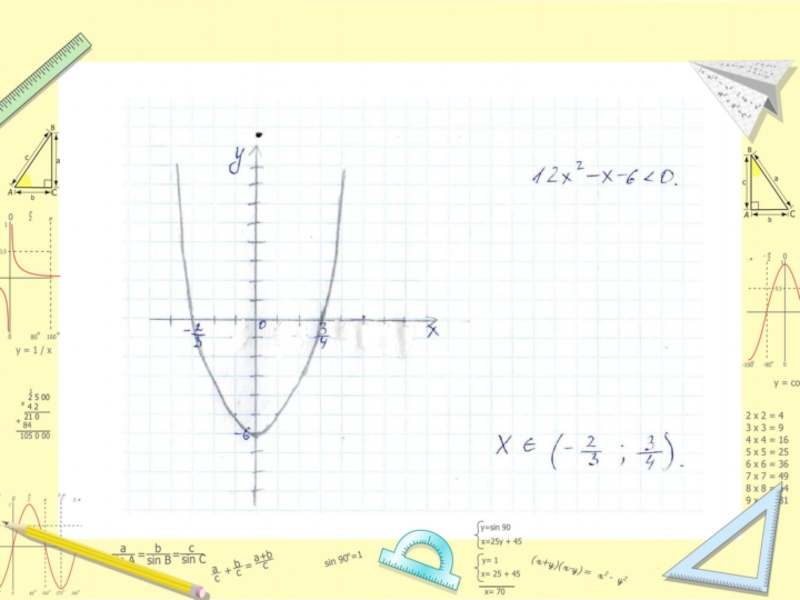
- 26. Слайд 26
- 27. Перепишем неравенство так: х^2-4>3х Построим графики функций:
- 28. Спасибо за внимание.
Цель моей работы : изложить графический метод решения уравнений и неравенств, который дает возможность определить корни или доказать ,что уравнение корней не имеет ( т.е. решением неравенства является пустое множество).
Слайд 1
Тема: «Графическое решение
уравнений и неравенств.»
Выполнила работу:
Лубошникова София,
ученица 9а
Слайд 2
Цель моей работы :
изложить графический метод решения уравнений и неравенств,
который дает возможность определить корни или доказать ,что уравнение корней не имеет ( т.е. решением неравенства является пустое множество).
Слайд 3 Актуальность темы:
графический метод, опирающийся на знания элементарных
функций, удобно применять при решении задач на нахождение числа корней
Слайд 4Алгоритм решения уравнений графическим способом.
1. Составить функции по левой и правой
части уравнения.
2. Составить таблицу значений каждой функции.
3. В одной системе координат построить графики этих функций .
4. Найти точки пересечения 2-х графиков.
5. Опустить из найденных точек на ось абсцисс перпендикуляры и найти значения (х).
6. Абсциссы точек пересечения – это корни уравнения. Записать их в ответ, используя знак приближённого равенства.
2. Составить таблицу значений каждой функции.
3. В одной системе координат построить графики этих функций .
4. Найти точки пересечения 2-х графиков.
5. Опустить из найденных точек на ось абсцисс перпендикуляры и найти значения (х).
6. Абсциссы точек пересечения – это корни уравнения. Записать их в ответ, используя знак приближённого равенства.
Слайд 5Графики основных функций:
у = k x + b -
прямая
у = k/x - гипербола
(x– a)^2+ (у – b)^2= r^2 - окружность с центром в точке с координатами (а, b)
y = a х^2 + b x + c - парабола.
у = k/x - гипербола
(x– a)^2+ (у – b)^2= r^2 - окружность с центром в точке с координатами (а, b)
y = a х^2 + b x + c - парабола.
Слайд 6 Графическое решение линейных уравнений
Задание :
Решить графическим способом уравнение
2x−10=2
Решение:
1 способ:
1)Перенесем слагаемые следующим образом:
2 x = 12.
2) Построим графики функций: y=2x и y=12.
Слайд 10Решим графическим способом уравнение: x^2 +2x−8=0
1 способ:
Перепишем уравнение в
виде:
x^2 =-2x+8
Построим графики функций:
y = x^2 и y =-2x+8
x^2 =-2x+8
Построим графики функций:
y = x^2 и y =-2x+8
Слайд 132 способ:
Перепишем уравнение в виде :x^2 – 8 = -2x
И построим графики функций:
y = x^2 – 8 и y = -2x
3 способ:
Перепишем уравнение в виде : x^2 +2x = 8
Построим графики функций:
y = x^2 + 2x и y = 8
Слайд 16Задание:
Решим уравнение: х^ 2 +2=0
Решение:
Перепишем уравнение в виде: х^ 2
= -2
Построим графики функций:
у = -2 и у = х^ 2
Построим графики функций:
у = -2 и у = х^ 2
Слайд 17 Построим графики функций: у=-2 и у= х^ 2
Графики
данных функций точек пересечения не имеют, следовательно уравнение решений не имеет.
Ответ : решений нет.
Ответ : решений нет.
Слайд 18Задание:
Решить графически уравнение: 3/х +2 = х
Решение:
Перепишем уравнение в виде:
3/х
= х – 2
Построим графики функций:
у = 3/х и у = х - 2
Построим графики функций:
у = 3/х и у = х - 2
Слайд 20Графики функций пересекаются в точках с координатами: (3;1) и (-1;-3).
Ответ: х = -1 ; х = 3
Слайд 21Задание:
Решить уравнение : 2 х^3 – x - 1=0
Решение:
Перепишем уравнение в
виде:
2 х^3 = x+1
Построим графики функций:
у = 2 х^3 и у = x+1
2 х^3 = x+1
Построим графики функций:
у = 2 х^3 и у = x+1
Слайд 23
Задание:
Решить уравнение: √ x - 0.5x=0
Перепишем уравнение в виде :
√ x = 0.5x
Построим графики функций:
у=0.5x и у = √ x
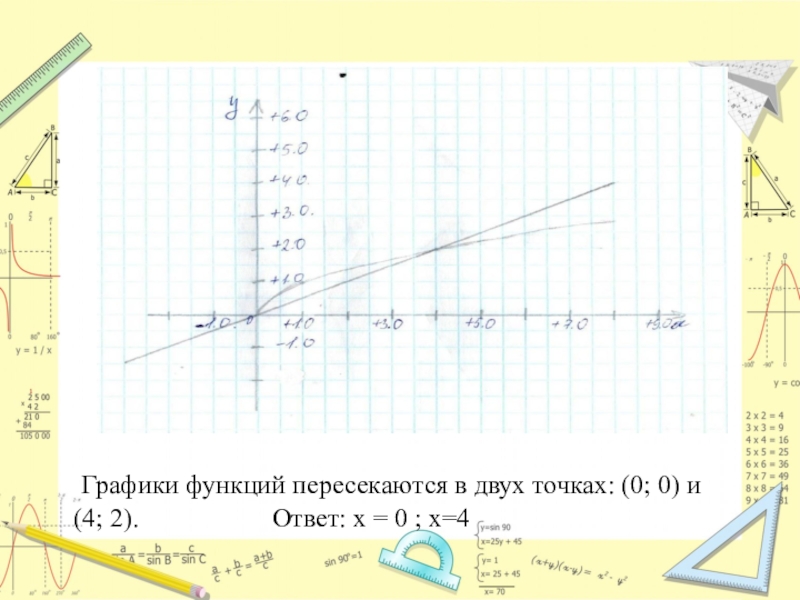
Построим графики функций:
у=0.5x и у = √ x
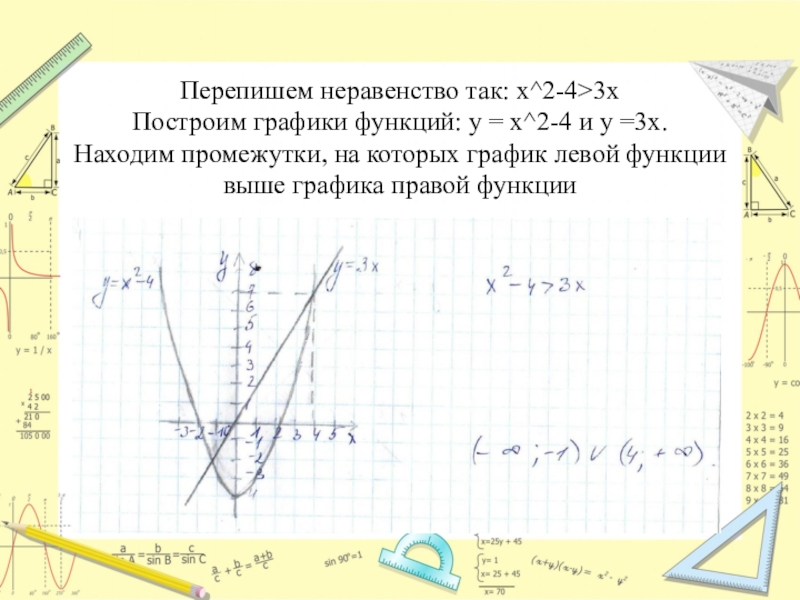
Слайд 27Перепишем неравенство так: х^2-4>3х Построим графики функций: у = х^2-4 и у
=3х.
Находим промежутки, на которых график левой функции выше графика правой функции