- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Решение неравенств методом декомпозиции
Содержание
- 1. Презентация Решение неравенств методом декомпозиции
- 2. Цели урока:Повторить решение рациональных неравенств методом интервалов;Обобщить
- 3. Выбрать ответОпределить знакНайти «нули» Отметить «нули» Выколоть «нули»
- 4. Назовите числа, при которых числитель и знаменатель будут равны нулю
- 5. Назовите выколотые и не выколотые точки
- 6. Назовите выколотые и невыколотые точки
- 7. При каких значениях х имеет смысл выражение?
- 8. Оптимальные способы решения неравенствРешение неравенств методом интерваловРешение
- 9. Решить неравенство:
- 10. Правильные ответы1. (-∞;4]U[5;8)2. (1;4)3. (-1;1)
- 11. Метод «Декомпозиции» При решении неравенств методом интерваловвычисление
- 12. Метод «декомпозиции» заключается взамене сложного выражения F(x)
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Домашняя работаLog(5х2-19) (10х-19)>1Log(2х2-5) (х-3)>0Log/х/ (х-5)>0Log(х2-4) (-4х-16)>1Log(х+5) (х-7)>0Log/х/ (х+7)>0
- 18. Кому принадлежит фраза
Цели урока:Повторить решение рациональных неравенств методом интервалов;Обобщить метод интервалов для решения дробно-рациональных неравенств;Закрепить полученные знания при решении практических задачПрименить полученные знания в новой ситуации.
Слайд 2Цели урока:
Повторить решение рациональных неравенств методом интервалов;
Обобщить метод интервалов для решения
дробно-рациональных неравенств;
Закрепить полученные знания при решении практических задач
Применить полученные знания в новой ситуации.
Закрепить полученные знания при решении практических задач
Применить полученные знания в новой ситуации.
Слайд 8Оптимальные способы решения неравенств
Решение неравенств методом интервалов
Решение неравенств с модулями и
с параметрами
Решение дробно-рациональных неравенств
Решение логарифмических неравенств (метод «декомпозиции»)
Решение тригонометрических неравенств
Решение дробно-рациональных неравенств
Решение логарифмических неравенств (метод «декомпозиции»)
Решение тригонометрических неравенств
Слайд 11Метод «Декомпозиции»
При решении неравенств методом интервалов
вычисление значений функций в
промежуточных точках может
вызвать
трудности вычислительного характера. С
другой стороны, для рациональных функций такие
вычисления несколько проще.
Чтобы расширить возможности применения
метода интервалов при решении неравенств,
используем идею рационализации неравенств,
известную в математической литературе под
другими названиями (метод декомпозиции –
Моденов В.П., метод замены множителей –
Голубев В.И.).
трудности вычислительного характера. С
другой стороны, для рациональных функций такие
вычисления несколько проще.
Чтобы расширить возможности применения
метода интервалов при решении неравенств,
используем идею рационализации неравенств,
известную в математической литературе под
другими названиями (метод декомпозиции –
Моденов В.П., метод замены множителей –
Голубев В.И.).
Слайд 12
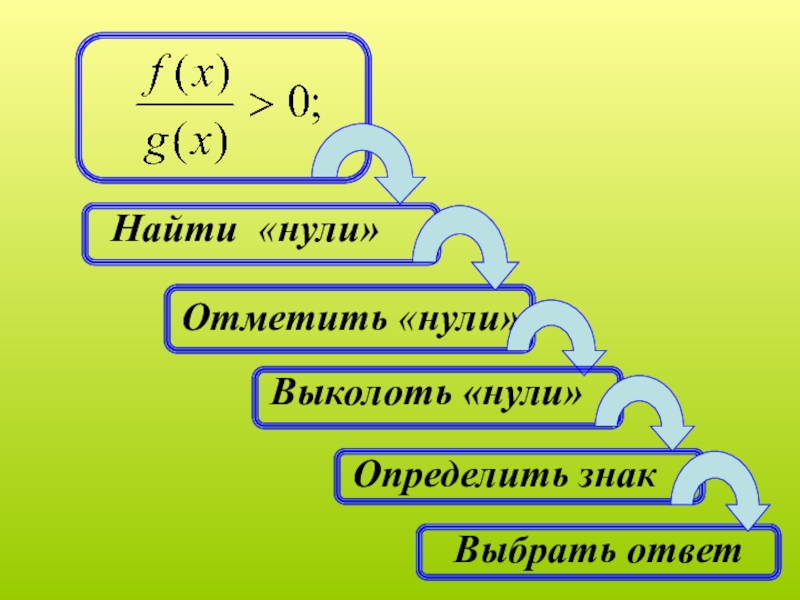
Метод «декомпозиции» заключается в
замене сложного выражения F(x) на бо-
лее простое выражение
G(x) (в конечном
счете, рациональное), при которой нера-
венство G(x)> 0 равносильно неравенству
F(x)> 0 в области определения выраже-
ния F(x) .
счете, рациональное), при которой нера-
венство G(x)> 0 равносильно неравенству
F(x)> 0 в области определения выраже-
ния F(x) .





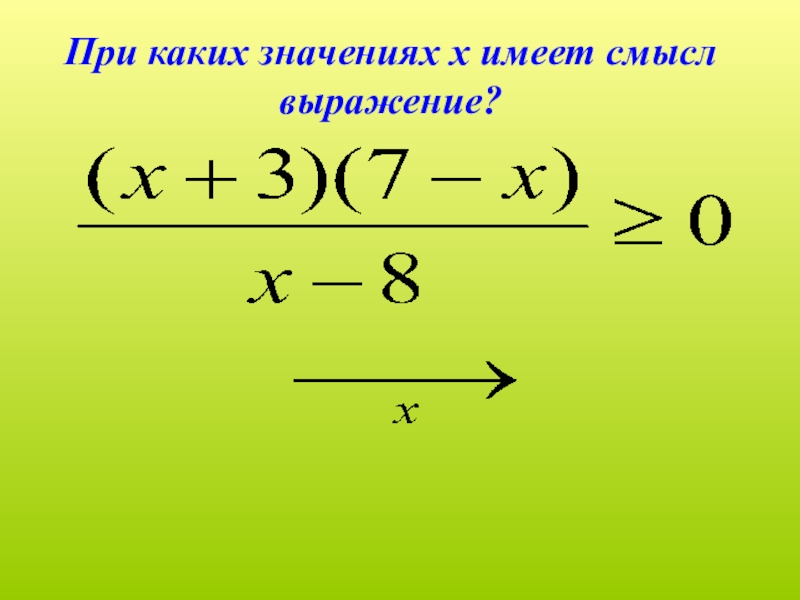

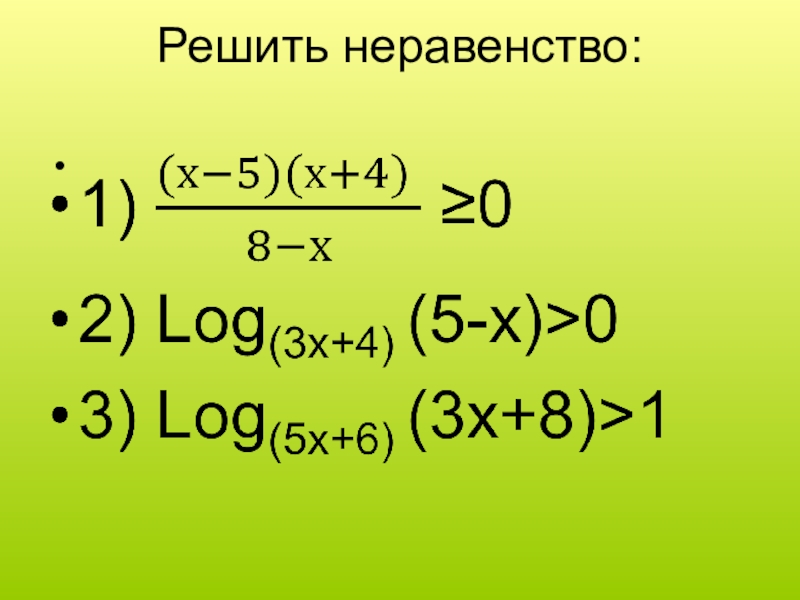
![Презентация Решение неравенств методом декомпозиции Правильные ответы1. (-∞;4]U[5;8)2. (1;4)3. (-1;1) Правильные ответы1. (-∞;4]U[5;8)2. (1;4)3. (-1;1)](/img/thumbs/e05914318575f17e9047d55056f03334-800x.jpg)