его корни».
Сурина Татьяна Михайловна
2013 – 2014 учебный год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Решение квадратных уравнений
Содержание
- 1. Презентация Решение квадратных уравнений
- 2. Цели:
- 3. Решение квадратных уравнений выделением квадрата двучлена часто
- 4. Число его корней зависит от знака дроби
- 5. Для квадратных уравнений, у которых второй коэффициент
- 6. x2 + px + q
- 7. Заполните пропуски в формулировке определений, свойств и
- 8. Определить истинны ли приведенные утверждения, выбрав ответ
- 9. 1) Пусть ax2 + bx +
- 10. 1. При каких значениях Х трехчлен
- 11. Литература: «Алгебра 8 класс», авторы Ю. Н.
- 12. Спасибо за внимание!
Цели: обобщить, повторить и закрепить знания по данной теме, подготовить учащихся к выполнению теста;
Слайд 2 Цели: обобщить, повторить и закрепить
знания
по данной теме, подготовить учащихся к выполнению теста;
развивать логическое мышление, быстроту,
сообразительность;
Слайд 3
Решение квадратных уравнений выделением квадрата двучлена часто приводит к громоздким преобразованиям.
Поэтому поступают иначе. Решают уравнение в общем виде и в результате получают формулу корней. Затем формулу применяют при решении любого квадратного уравнения.
Решим уравнение ax2 + bx + c = 0.
Разделив обе его части на a , получим равносильное ему приведенное квадратное уравнение
(1)
Преобразуем это уравнение
(2)
Уравнение (2) равносильно уравнению (1).
Решим уравнение ax2 + bx + c = 0.
Разделив обе его части на a , получим равносильное ему приведенное квадратное уравнение
(1)
Преобразуем это уравнение
(2)
Уравнение (2) равносильно уравнению (1).
Слайд 4
Число его корней зависит от знака дроби
Так как a ≠ 0, то 4a2 - положительное число, поэтому знак этой дроби определяется знаком ее числителя, т.е. выражения b2 – 4ac Это выражение называют дискриминантом квадратного уравнения ax2 + bx + c = 0. Его обозначают буквой D, т.е. D = b2 – 4ac
ВОЗМОЖНЫЕ СЛУЧАИ ЗАВИСИМОСТИ ОТ D
Если D > 0, то выражение имеет 2 корня
Если D = 0, то в этом случае выражение имеет один корень
Если D < 0, то выражение корней не имеет
Слайд 5
Для квадратных уравнений, у которых второй коэффициент является четным числом, формулу
корней удобно записать в другом виде.
Рассмотрим квадратное уравнение
ax2 + 2kx + c = 0
Найдем его дискриминант: D = 4k2 – 4ac = 4 (k2 – ac)
Очевидно, что число корней уравнения зависит от знака выражения k2 – ac. Обозначим это выражение через D1
Если D1 ≥0, то по формуле корней квадратного уравнения получим, что
Т.е. , где D1 = k2 – ac
Если D1 < 0 то уравнение корней не имеет
Рассмотрим квадратное уравнение
ax2 + 2kx + c = 0
Найдем его дискриминант: D = 4k2 – 4ac = 4 (k2 – ac)
Очевидно, что число корней уравнения зависит от знака выражения k2 – ac. Обозначим это выражение через D1
Если D1 ≥0, то по формуле корней квадратного уравнения получим, что
Т.е. , где D1 = k2 – ac
Если D1 < 0 то уравнение корней не имеет
Слайд 6
x2 + px + q = 0 - приведенное квадратное
уравнение
Корни приведенного квадратного уравнения равны половине второго коэффициента, взятого с противоположным знаком ± корень квадратный из квадрата этой половины без свободного члена
Корни приведенного квадратного уравнения равны половине второго коэффициента, взятого с противоположным знаком ± корень квадратный из квадрата этой половины без свободного члена
Слайд 7Заполните пропуски в формулировке определений, свойств и в истинных утверждениях. а)
Квадратным трехчленом называется многочлен вида __________________,
где х – переменная, ________- некоторые числа, причем а ≠ 0.
б)Дискриминант квадратного уравнения находят по формуле D = ____________.
в)Корни квадратного уравнения находят по формуле х₁,₂ = _________________.
г) Дискриминант квадратного уравнения
ах² + 2kx+c=0, находят по формуле
D1 =______________________.
д)Если х₁ и х₂ - корни квадратного трехчлена, то можно разложить на множители по формуле ах² + bх + с = _________________.
Слайд 8Определить истинны ли приведенные утверждения, выбрав ответ да или нет. 1. Если
дискриминант квадратного трехчлена больше нуля, то квадратный трехчлен имеет два корня.
1) да; 2) нет.
2. Число 2 является корнем квадратного трехчлена х² + 3х – 10.
1) да; 2) нет.
3. Число 3 является корнем квадратного трехчлена х² - х – 12.
1) да; 2) нет.
4. Данный трехчлен можно разложить на множители так:
х² - 9х – 22 = (х + 11) (х + 2), если корни его 11 и – 2.
1) да; 2) нет.
5. Данный трехчлен можно разложить на множители так:
5х² - 8х – 4 = (х – 2) (х + 0,4), если корни его 2 и -0,4.
1) да; 2) нет.
Слайд 9
1) Пусть ax2 + bx + c = 0 квадратное уравнение,
сумма коэффициентов которого равна нулю, т.е. a + b + c = 0,
Тогда его корни находят по формулам x1 = 1; x2 =
Например, уравнение 2005 x2 – 1996 x – 9 = 0 имеем корни
x1 = 1; x2 = т.к. 2005 + (- 1996 ) – 9 = 0
2) Если в уравнении ax2 + bx + c = 0 коэффициенты такие, что
a + c = b , то x1 = - 1; x2 =
Например: 1997 x2 – 2000 x + 3 = 0
1997 + 3 = 2000 , значит x1 = - 1; x2 =
Тогда его корни находят по формулам x1 = 1; x2 =
Например, уравнение 2005 x2 – 1996 x – 9 = 0 имеем корни
x1 = 1; x2 = т.к. 2005 + (- 1996 ) – 9 = 0
2) Если в уравнении ax2 + bx + c = 0 коэффициенты такие, что
a + c = b , то x1 = - 1; x2 =
Например: 1997 x2 – 2000 x + 3 = 0
1997 + 3 = 2000 , значит x1 = - 1; x2 =
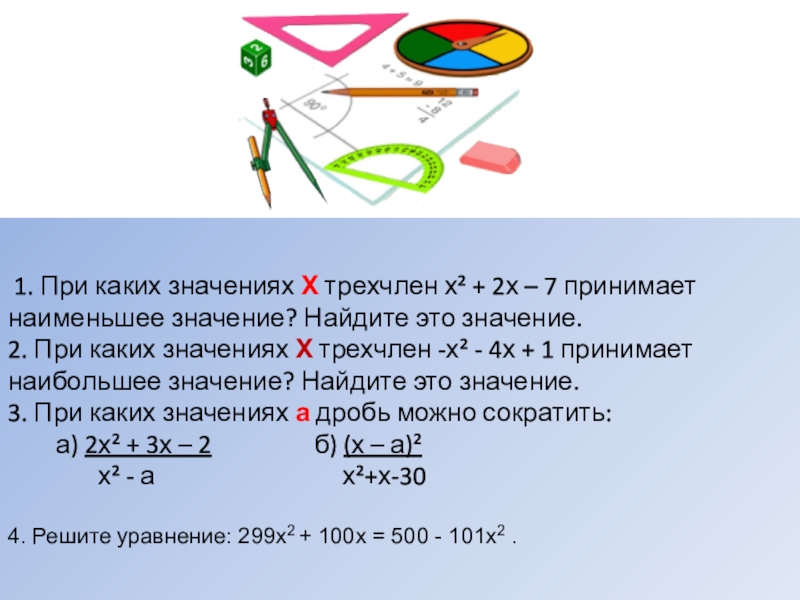
Слайд 10 1. При каких значениях Х трехчлен х² + 2х –
7 принимает наименьшее значение? Найдите это значение.
2. При каких значениях Х трехчлен -х² - 4х + 1 принимает наибольшее значение? Найдите это значение.
3. При каких значениях а дробь можно сократить:
а) 2х² + 3х – 2 б) (х – а)²
х² - а х²+х-30
4. Решите уравнение: 299x2 + 100x = 500 - 101x2 .
Слайд 11Литература: «Алгебра 8 класс», авторы Ю. Н. Макарычев, Н. Г. Миндюк, К.
И. Нешков, С. Б. Суворова, Москва «Просвещение», 2009.
Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы «Алгебра», авторы Л. В. Кузнецова, Е. А. Буминович, Б. П. Пигарев, С. Б. Суворова, «Дрофа», Москва, 2011.
Интернет ресурсы:
schooloz25.ucos.ru
86licei-nv.edusite.ru
mamindnevnichor.ru
matem.ege2012a.ru