- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проекта История математики
Содержание
- 1. Презентация проекта История математики
- 2. Математика900igr.net
- 3. История математикиМатема́тика ( — наука о структурах, порядке и
- 4. Как появилась математика «Математика» произошло от древне-греческого
- 5. Разделы математики Математика как учебная дисциплина подразделяется
- 6. Математика в разное времяАкадемиком А. Н. Колмогоровым предложена такая
- 7. Кипу, использовались инками для записи чисел
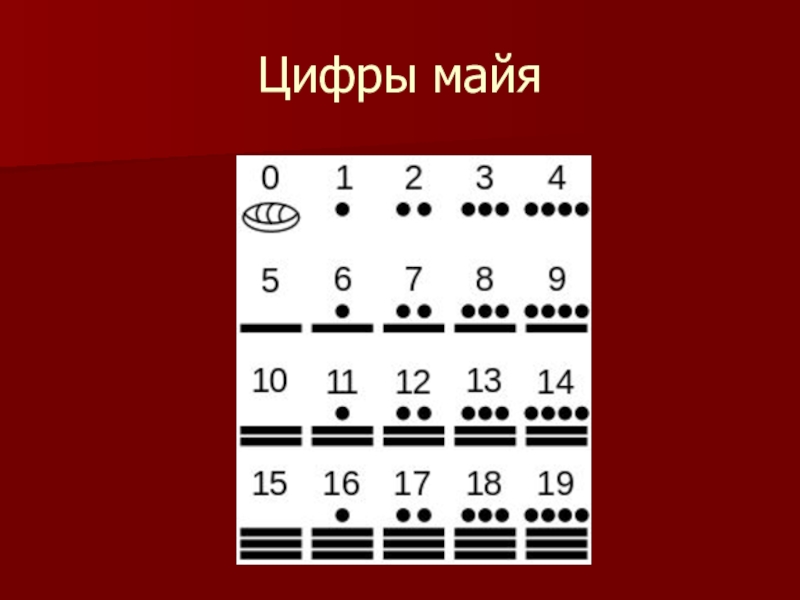
- 8. Цифры майя
- 9. Великие математикиМатема́тик — учёный, чьи научные исследования в основном посвящены математике.
- 10. М.В.Остроградский Михаил Васильевич Остроградский (1801-1861/62)
- 11. Блез Паскаль Блез Паскаль (1623-1662)
- 12. Исаак Ньютон Исаак Ньютон (1643-1727)
- 13. Рене Декарт Рене Декарт (1596-1650)
- 14. Интересные факты Используемая нами десятичная система
- 15. Листья на ветке растения всегда
- 16. Существует математический закон Бенфорда, который гласит,
- 17. Слайд 17
Математика900igr.net
Слайд 3История математики
Матема́тика ( — наука о структурах, порядке и отношениях, которая исторически сложилась
на основе операций подсчёта, измерения и описания форм реальных объектов. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке. Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов. Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы.
Слайд 4Как появилась математика
«Математика» произошло от древне-греческого μάθημα (máthēma), что означает
изучение, знание, наука, и др.-греч. μαθηματικός (mathēmatikós), первоначально означающего восприимчивый, успевающий, позднее относящийся к изучению, впоследствии относящийся к математике. В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год).
Слайд 5Разделы математики
Математика как учебная дисциплина подразделяется в Российской Федерации на
элементарную математику, изучаемую в средней школе и образованную дисциплинами:
арифметика,
элементарная алгебра
элементарная геометрия: планиметрия и стереометрия
теория элементарных функций и элементы анализа
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
арифметика,
элементарная алгебра
элементарная геометрия: планиметрия и стереометрия
теория элементарных функций и элементы анализа
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
Слайд 6Математика в разное время
Академиком А. Н. Колмогоровым предложена такая структура истории математики:
Период зарождения
математики, на протяжении которого был накоплен достаточно большой фактический материал;
Период элементарной математики, начинающийся в VI—V веках до н. э. и завершающийся в конце XVI века («Запас понятий, с которыми имела дело математика до начала XVII века, составляет и до настоящего времени основу „элементарной математики“, преподаваемой в начальной и средней школе»);
Период математики переменных величин, охватывающий XVII—XVIII века, «который можно условно назвать также периодом „высшей математики“»;
Период современной математики — математики XIX—XX века, в ходе которого математикам пришлось «отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм».
Период элементарной математики, начинающийся в VI—V веках до н. э. и завершающийся в конце XVI века («Запас понятий, с которыми имела дело математика до начала XVII века, составляет и до настоящего времени основу „элементарной математики“, преподаваемой в начальной и средней школе»);
Период математики переменных величин, охватывающий XVII—XVIII века, «который можно условно назвать также периодом „высшей математики“»;
Период современной математики — математики XIX—XX века, в ходе которого математикам пришлось «отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм».
Слайд 9Великие математики
Матема́тик — учёный, чьи научные исследования в основном посвящены математике.
Слайд 10М.В.Остроградский
Михаил Васильевич Остроградский (1801-1861/62)
Русский математик – один
из основателей Петербургской математической школы , академик Петербургской академии наук. Занимался внешней баллистикой, статистическими методами браковки изделий, участвовал в комиссиях по реформе календаря и водоснабжению Петербурга. Основные труды в области прикладной математики.
Слайд 11Блез Паскаль
Блез Паскаль (1623-1662)
Французский математик,
физик, философ, писатель. Родился в семье юриста, занимающегося математикой. Рано проявил математические способности. Имеет трактат Опыт о конических сечениях. Сконструировал суммирующую машину. Имеет работы по теории чисел, арифметике, теории вероятностей. Нашёл общий алгоритм для нахождения признаков делимости чисел. Имеет трактат об «Арифметическом треугольнике». Установил принцип действия жидкостей и газов. Написал «Письма к провинциалу»- шедевр французской сатирической прозы.
Слайд 12Исаак Ньютон
Исаак Ньютон (1643-1727)
Великий английский учёный. Одновременно
с Лейбницем разработал основы математического анализа. Создатель классической механики. Ньютону принадлежат выдающиеся открытия в оптике, других разделах физики и математики. Главный его труд –«Математические начала натуральной философии»- оказал колоссальное на развитие естествознания.
Слайд 13Рене Декарт
Рене Декарт (1596-1650)
Французский математик и философ.
В начале тринадцатилетней войны служил в армии. Позже поселился в Нидерландах и в уединении занялся наукой. По приглашению шведской королевы переселился в Стокгольм. Заложил основы аналитической геометрии, дал понятие импульса силы, вывел закон сохранения количества движения, создал метод координат ( декартовы координаты). Известны кривые овалы Декарта. В основе его философии дуализм души и тела.
Слайд 14Интересные факты
Используемая нами десятичная система счисления возникла по причине
того, что у человека на руках 10 пальцев. Способность к абстрактному счёту появилась у людей не сразу, а использовать для счёта именно пальцы оказалось удобнее всего. Цивилизация майя и независимо от них чукчи исторически использовали двадцатичную систему счисления, применяя пальцы не только рук, но и ног. В основе распространённых в древних Шумере и Вавилоне двенадцатеричной и шестидесятиричной систем тоже было использование рук: большим пальцем отсчитывались фаланги других пальцев ладони, число которых равно 12.
Слайд 15
Листья на ветке растения всегда располагаются в строгом порядке,
отстоя друг от друга на определённый угол по или против часовой стрелки. Величина угла разная у различных растений, но её всегда можно описать дробью, в числителе и знаменателе которой — числа из ряда Фибоначчи. Например, у бука этот угол равен 1/3, или 120°, у дуба и абрикоса — 2/5, у груши и тополя — 3/8, у ивы и миндаля — 5/13 и т.д. Такое расположение позволяет листьям наиболее эффективно получать влагу и солнечный свет.
Слайд 16
Существует математический закон Бенфорда, который гласит, что распределение первых цифр
в числах каких-либо наборов данных из реального мира неравномерно. Цифры от 1 до 4 в таких наборах (а именно статистика рождаемости или смертности, номера домов и т.п.) на первой позиции встречаются гораздо чаще, чем цифры от 5 до 9. Практическое применение этого закона заключается в том, что по нему можно проверять на достоверность бухгалтерские и финансовые данные, результаты выборов и многое другое. В некоторых штатах США несоответствие данных закону Бенфорда даже является формальной уликой в суде.