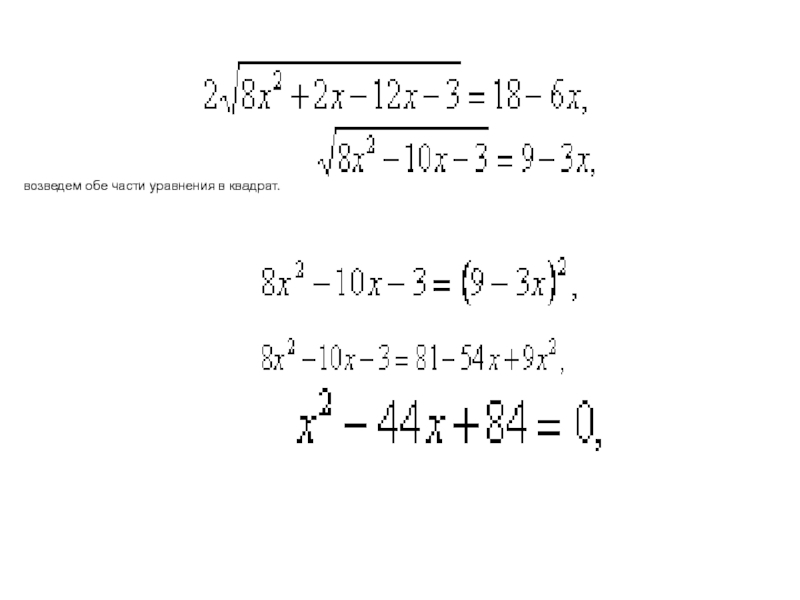Ученица 11 класса
Шеметова Алиса
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проект по математике на тему Проект Метод возведения обеих частей уравнения в одну и ту же степень с последующей проверкой иррациональных уравнений
Содержание
- 1. Презентация- проект по математике на тему Проект Метод возведения обеих частей уравнения в одну и ту же степень с последующей проверкой иррациональных уравнений
- 2. Методы решения иррациональных уравненийТворческое задание №2. (Индивидуальная
- 3. Способ I. Метод возведения обеих частей уравнения
- 4. возведем обе части уравнения в квадрат.
- 5. По теореме Виета:Проверка:1) Если х=42, то Значит, число 42 не является корнем уравнения.
- 6. 2) Если х=2, тоЗначит, число 2 является корнем уравнения.Ответ: 2
- 7. Вывод: При решении иррациональных уравнений методом возведения обеих
Методы решения иррациональных уравненийТворческое задание №2. (Индивидуальная работа.) Решить уравнение различными способами. Оценить достоинства и недостатки каждого способа. Оформить запись выводов в виде таблицы.
Слайд 1Проект I. Метод возведения обеих частей уравнения в одну и ту
же степень с последующей проверкой
Слайд 2Методы решения иррациональных уравнений
Творческое задание №2. (Индивидуальная работа.) Решить уравнение различными
способами. Оценить достоинства и недостатки каждого способа. Оформить запись выводов в виде таблицы.
Слайд 3Способ I. Метод возведения обеих частей уравнения в одну и ту
же степень с последующей проверкой
+
=4,
возведем обе части уравнения в квадрат.
,
Слайд 7Вывод: При решении иррациональных уравнений методом возведения обеих частей уравнения в одну
и туже степень необходимо вести словесную запись, что делает решение понятным и доступным. Однако обязательная проверка иногда бывает громоздкой и занимает много времени. Этот метод можно использовать для несложных иррациональных уравнений, содержащих 1-2 радикала.