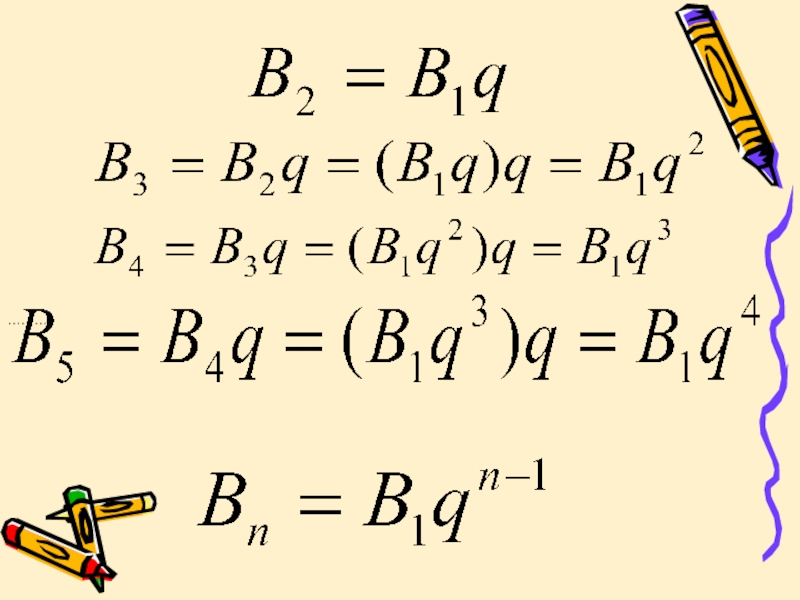- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Геометрическая прогрессия (9 класс)
Содержание
- 1. Презентация по алгебре на тему Геометрическая прогрессия (9 класс)
- 2. Рассмотрим последовательность: 2; 4; 8; 16; 32;
- 3. Рассмотрим последовательность: 2; 8; 32; 128; 512;
- 4. Геометрической прогрессией называется последовательность отличных от
- 5. ………
- 6. Задание 1. Дано: (bn ) -
- 7. Задание 2. Выберите из последовательностей геометрические прогрессии.
- 8. Задание 3. В геометрической прогрессии
- 9. Задание 4.Дано: (bn ) - геометрическая прогрессия
- 10. Задание 5.Найти пятый член геометрической прогрессии: 2;
- 11. Слайд 11
- 12. Найдите восьмой член геометрической прогрессии 3,2; 1,6; 0,8; … .Задание 6Ответ: 0,025
- 13. Какая из последовательностей не является геометрической прогрессией?Задание
Рассмотрим последовательность: 2; 4; 8; 16; 32; … a1 =2 a2 =4 a3 =8 …Каждый последующий член последовательности равен предыдущему члену, умноженному на 2.
Слайд 2Рассмотрим последовательность:
2; 4; 8; 16; 32; …
a1 =2
a2 =4
a3 =8
…
Каждый последующий член последовательности равен предыдущему члену, умноженному на 2.
Слайд 3Рассмотрим последовательность:
2; 8; 32; 128; 512; …
a1 =2
a2 =8
a3 =32
…
Каждый последующий член последовательности равен предыдущему члену, умноженному на 4.
Слайд 4
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член
которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
Иначе, последовательность (вn)- геометрическая прогрессия, если для любого натурального n
выполняется условие и ,
где
Иначе, последовательность (вn)- геометрическая прогрессия, если для любого натурального n
выполняется условие и ,
где
Слайд 6
Задание 1.
Дано: (bn ) - геометрическая прогрессия
b1= 5
q = 3
Найти: b3 ; b5.
Решение: используя формулу bn = b1 q n-1
b3 =b1q2 = 5 . 32 =5 . 9=45
b5 =b1q4 = 5 . 34 =5 . 81=405
Ответ:45; 405.
Найти: b3 ; b5.
Решение: используя формулу bn = b1 q n-1
b3 =b1q2 = 5 . 32 =5 . 9=45
b5 =b1q4 = 5 . 34 =5 . 81=405
Ответ:45; 405.
Слайд 7Задание 2.
Выберите из последовательностей геометрические прогрессии.
А) 3; 6; 9;
12…
Б) 5; 5; 5; …
В) 1;2;4;8;16;
Г) -2; 2; -2; 2…
Б) 5; 5; 5; …
В) 1;2;4;8;16;
Г) -2; 2; -2; 2…
Слайд 8Задание 3.
В геометрической прогрессии =
13, 4 и q=0,2. Найти
Решение.
По формуле n-ого члена геометрической прогрессии
Решение.
По формуле n-ого члена геометрической прогрессии
Слайд 9Задание 4.
Дано: (bn ) - геометрическая прогрессия
b1= -2, b4=-54.
Найти:
q.
Решение: используя формулу bn = b1 q n-1
b4 =b1q3 ; -54=(-2) q3; q3= -54:(-2)=27;
q=3
Ответ: 3.
Решение: используя формулу bn = b1 q n-1
b4 =b1q3 ; -54=(-2) q3; q3= -54:(-2)=27;
q=3
Ответ: 3.
Слайд 10Задание 5.
Найти пятый член геометрической прогрессии: 2; -6…
Решение.
Зная первый и второй
члены геометрической прогрессии, можно найти её знаменатель.
q= -6:2= -3.
Таким образом
q= -6:2= -3.
Таким образом
Слайд 13Какая из последовательностей не является геометрической прогрессией?
Задание 7
А) -3; 6; -12;
24; -48
Б) 50; 10; 2; 0,4; 0,08
В) 64; 32; 8; 4; 1