- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Параметры
Содержание
- 1. Презентация по математике Параметры
- 2. Календарно-тематическое планирование элективного курса
- 3. Основные типы задач с параметрами
- 4. Основные методы решения задач с параметрами
- 5. Слайд 5
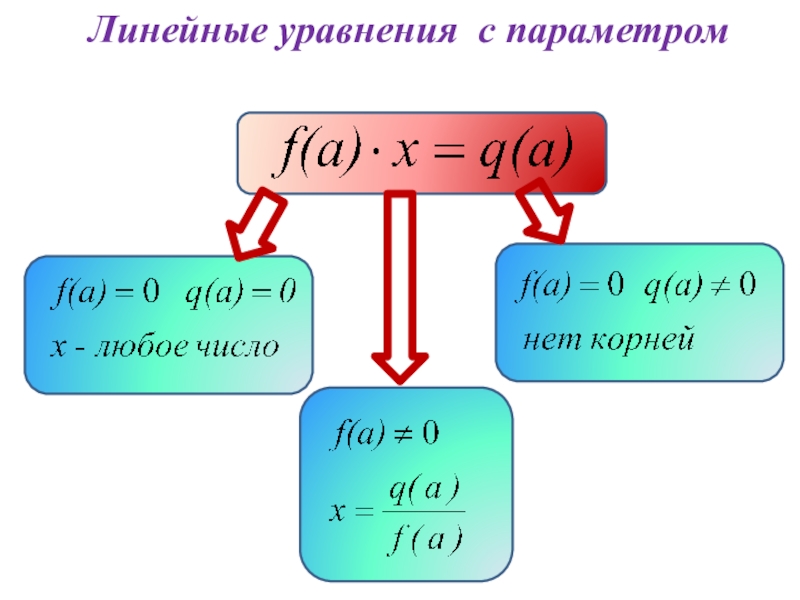
- 6. Линейные уравнения с параметром
- 7. Решить уравнение при всех значениях параметраПреобразуем уравнение
- 8. Примерная система упражнений
- 9. Найти все значения параметра а, при которых
- 10. Квадратные уравнения с параметром
- 11. Что можно сказать о знаках параметров a,b
- 12. При каких значениях параметра корни трехчлена
- 13. При каких значениях параметра корни трехчлена
- 14. Опорная схема «расположение корней квадратного трехчлена»
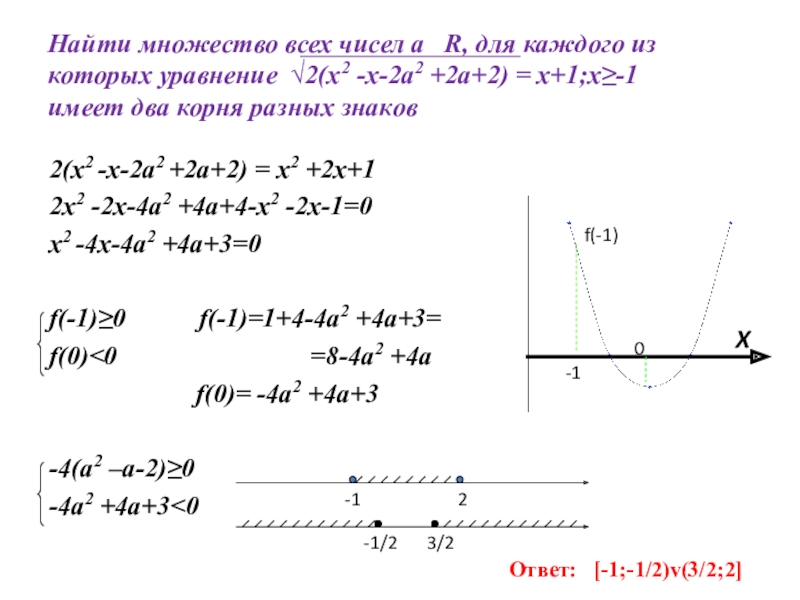
- 15. Найти множество всех чисел а R,
- 16. Примерная система упражнений
- 17. Кубические уравнения с параметром
- 18. Слайд 18
- 19. Уравнение имеет корень х=1. Найти остальные корни
- 20. Определить, при каких значениях параметра а
- 21. Уравнение
- 22. Определить все значения параметра а, при которых уравнение имеет один корень.
- 23. Задать формулой «семейство» графиковУ=lхl+а, а≤0а0ху0хувх²+(у-в)²=25, где (0;в)-центр50хаlхl+lуl=а, а≥00хуаУ=√а²-х²у0ху0хуху
- 24. МЕТОД ОБЛАСТЕЙ ПРИ РЕШЕНИИ ЗАДАЧ С ПАРАМЕТРАМИКлюч
- 25. Найти все значения а, при которых уравнение
- 26. Данное уравнение равносильно совокупности следующих двух уравнений:По
- 27. ху- 2- 44Найдите все значения параметра а,
- 28. («переход» метода интервалов с прямой на плоскость)1.
- 29. Граничные линии: Строим граничные линии. Они разбивают
- 30. Сколько решений имеет система в зависимости от
- 31. Найти все значения параметра р, при каждом
- 32. При каких положительных значениях параметра а, система
- 33. Найти все значения параметра а при каждом
- 34. При а = 3, «вершина уголка»; Найти
Слайд 1Мастер-класс
МОУ СОШ № 13
Учитель математики Шачнева Людмила Анатольевна
Решение уравнений и
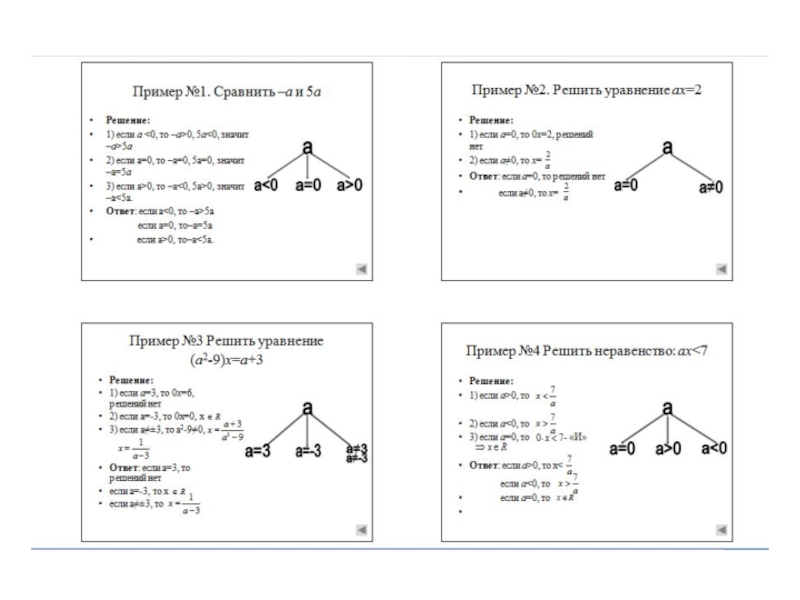
Слайд 7Решить уравнение при всех значениях параметра
Преобразуем уравнение к виду
не определена при
при а=2 получаем уравнение 0х=0 – х любое число
при а=3 получаем уравнение 0х=1 – корней нет
Во всех остальных случаях
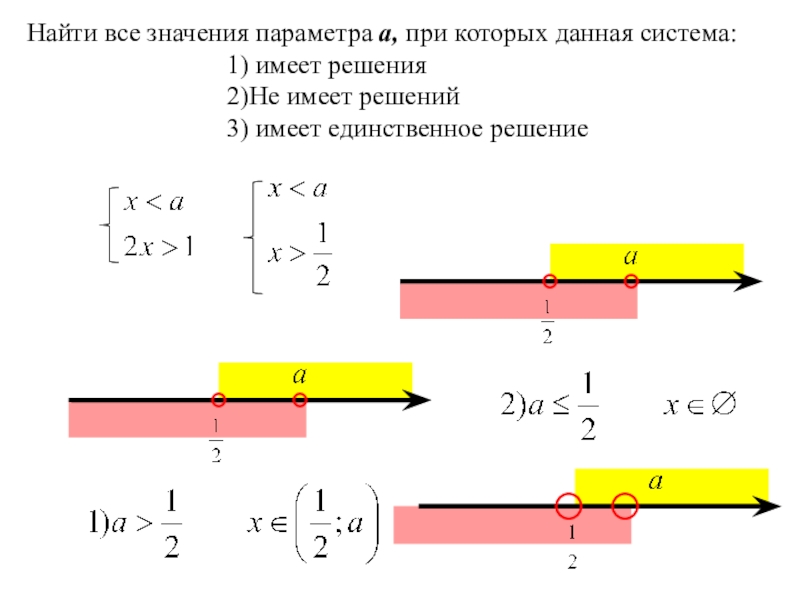
Слайд 9Найти все значения параметра а, при которых данная система:
1) имеет решения
2)Не
3) имеет единственное решение
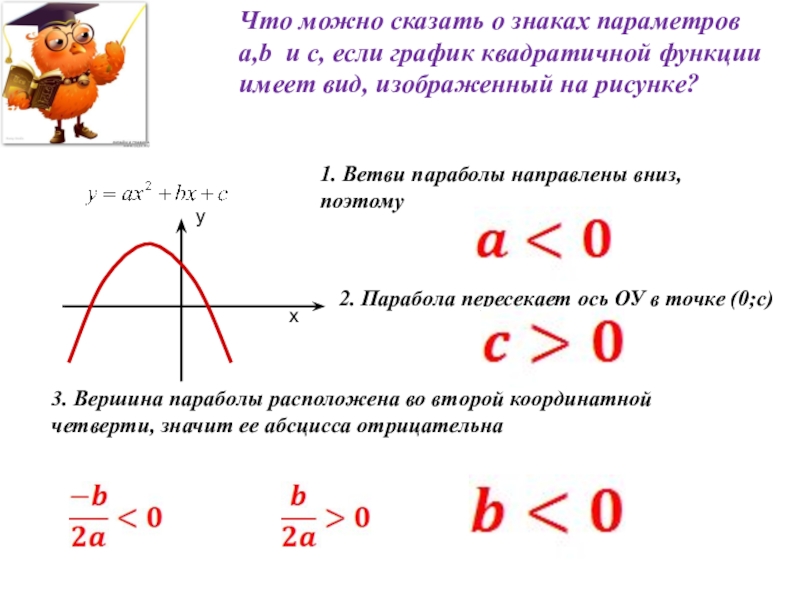
Слайд 11Что можно сказать о знаках параметров a,b и c, если график
х
у
1. Ветви параболы направлены вниз, поэтому
2. Парабола пересекает ось ОУ в точке (0;с)
3. Вершина параболы расположена во второй координатной четверти, значит ее абсцисса отрицательна
Слайд 12При каких значениях параметра корни трехчлена
1 способ
2 способ
1.При а=2 трехчлен превращается в линейный двучлен
2.Пусть а 2.
Тoгда
При a>6 корней у трехчлена нет
При a=6
3. При a<6 (но а 2) существуют два корня и нам надо выяснить когда они положительны
Ответ:
1.При а=2 трехчлен превращается в линейный двучлен
2.Пусть а 2
По теореме Виета
Ответ:
Слайд 13При каких значениях параметра корни трехчлена
3 способ
1.При а=2 трехчлен превращается в линейный двучлен
2.Пусть а 2. Рассмотрим функцию
у
х
3.Парабола пересекает ось ОХ в двух точках. Значит
4.Парабола пересекает ось ОУ в точке (0;с). Значит
5.Вершина параболы лежит в первой четверти. Значит
Слайд 15Найти множество всех чисел а R, для каждого из которых
2(x2 -x-2a2 +2a+2) = x2 +2x+1
2x2 -2x-4a2 +4a+4-x2 -2x-1=0
x2 -4x-4a2 +4a+3=0
f(-1)≥0 f(-1)=1+4-4a2 +4a+3=
f(0)<0 =8-4a2 +4a
f(0)= -4a2 +4a+3
-4(a2 –a-2)≥0
-4a2 +4a+3<0
X
-1
f(-1)
0
-1
2
-1/2
3/2
Ответ: [-1;-1/2)v(3/2;2]
Слайд 19Уравнение
имеет корень х=1. Найти остальные корни этого уравнения.
Воспользуемся теоремой
Из второго уравнения получаем а=-2, а=3.
При а=3 корни уравнения -5, 1, 1
При а=-2 корни уравнения 1,
Слайд 20Определить, при каких значениях параметра
а уравнение
имеет ровно два
Если кубическое ур-е имеет 2 корня, то это значит, что оно имеет 3 корня, два из которых равны.
Ответ: а= - 41; а= 84
Слайд 23Задать формулой «семейство» графиков
У=lхl+а, а≤0
а
0
х
у
0
х
у
в
х²+(у-в)²=25, где (0;в)-центр
5
0
х
а
lхl+lуl=а, а≥0
0
х
у
а
У=√а²-х²
у
0
х
у
0
х
у
х
у
Слайд 24МЕТОД ОБЛАСТЕЙ ПРИ РЕШЕНИИ ЗАДАЧ С ПАРАМЕТРАМИ
Ключ решения:
Графический прием
Свойства функций
Параметр –
Общие признаки задач подходящих
под рассматриваемый метод
В задаче дан один
параметр а и одна
переменная х
Они образуют некоторые
аналитические выражения
F (x;a), G (x;a)
Графики уравнений
F(x;a)=0,G(x;a)=0
строятся несложно
1.Строим графический образ
2.Пересекаем полученный график прямыми
перпендикулярными параметрической оси
3.«Считываем» нужную информацию
Схема
решения:
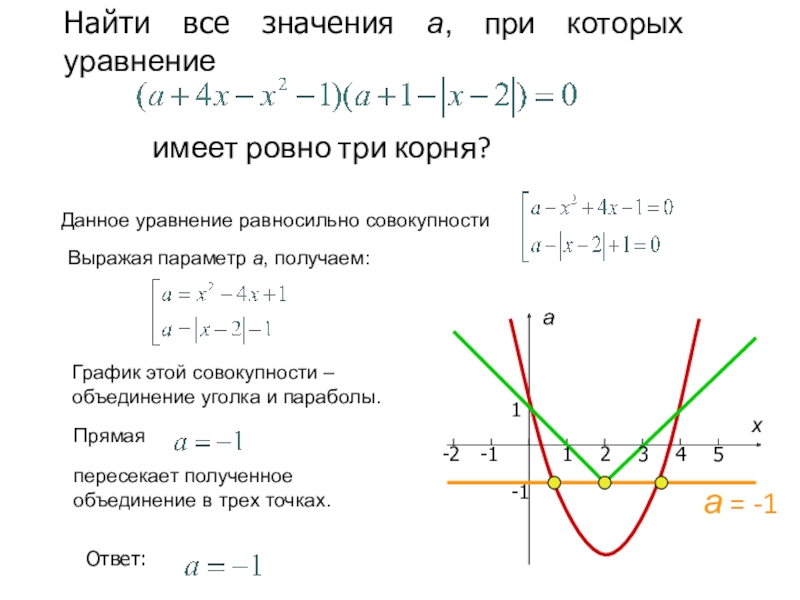
Слайд 25Найти все значения а, при которых уравнение
Данное уравнение равносильно совокупности
Выражая
График этой совокупности –
объединение уголка и параболы.
пересекает полученное
объединение в трех точках.
имеет ровно три корня?
Ответ:
1
2
3
4
5
-1
-2
-1
1
х
а
а = -1
Прямая
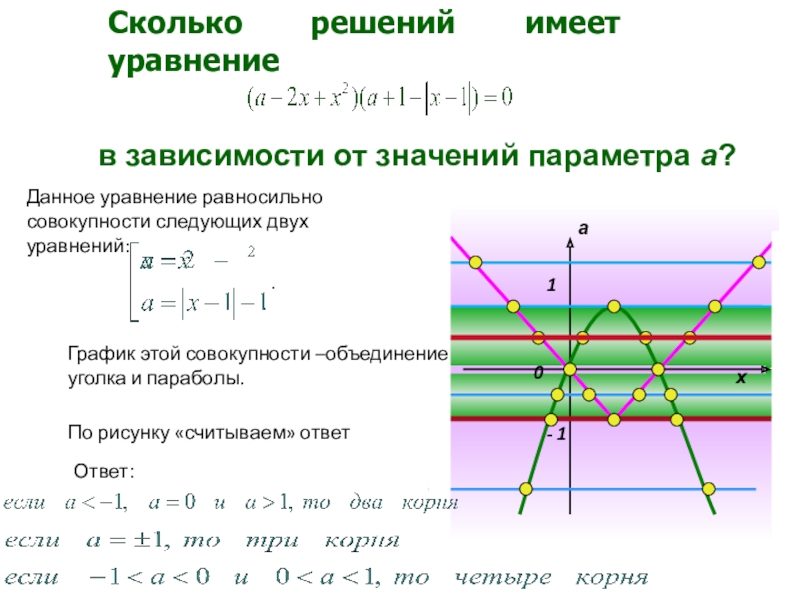
Слайд 26Данное уравнение равносильно совокупности следующих двух уравнений:
По рисунку «считываем» ответ
х
а
0
- 1
1
Ответ:
Сколько
в зависимости от значений параметра а?
График этой совокупности –объединение уголка и параболы.
Слайд 27х
у
- 2
- 4
4
Найдите все значения параметра а, при которых уравнение
2
А
В
А(-4; 0), В(-2; 0) и координаты этих точек удовлетворяют уравнению
-1
Слайд 28(«переход» метода интервалов с прямой на плоскость)
1. ОДЗ
2. Граничные линии
3. Координатная
плоскость
4. Знаки в областях
5.Ответ по рисунку.
1.ОДЗ
2. Корни
3. Ось
4. Знаки на
интервалах
5. Ответ.
Метод интервалов:
Метод областей:
ОБОБЩЕННЫЙ МЕТОД ОБЛАСТЕЙ
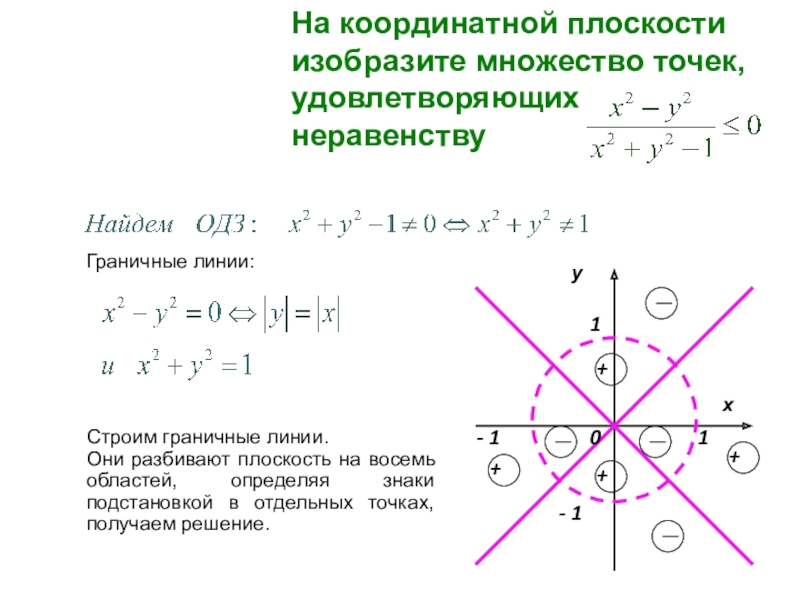
Слайд 29Граничные линии:
Строим граничные линии.
Они разбивают плоскость на восемь областей,
- 1
- 1
1
1
х
у
0
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству
Слайд 30Сколько решений имеет система
в зависимости от параметра а?
2
-2
2
-2
1
-1
1
Графиком второго
4 решения при а = 1
Ответ:
решений нет, если
8 решений, если
4 решения, если
Слайд 31Найти все значения параметра р, при каждом из которых
множество решений неравенства
не содержит ни одного решения неравенства
.
Применим обобщенный метод областей.
Определим знаки в полученных областях, и получим решение данного неравенства.
По рисунку легко считываем ответ
Ответ:
Построим граничные линии
р = 3
р = 0
-1
1
2
3
1
2
Слайд 32При каких положительных значениях параметра а, система уравнений имеет ровно четыре
и симметрично отображаем относительно оси абсцисс.
Второе уравнение задает семейство окружностей с центром (2;0) и радиусом а.
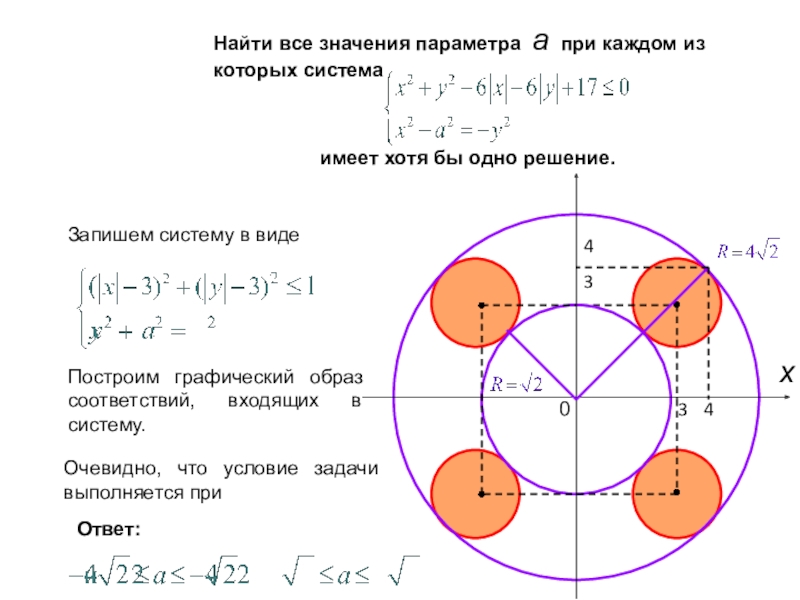
Слайд 33Найти все значения параметра а при каждом из которых система
имеет
Запишем систему в виде
Построим графический образ соответствий, входящих в систему.
3
3
4
4
Очевидно, что условие задачи выполняется при
Ответ:
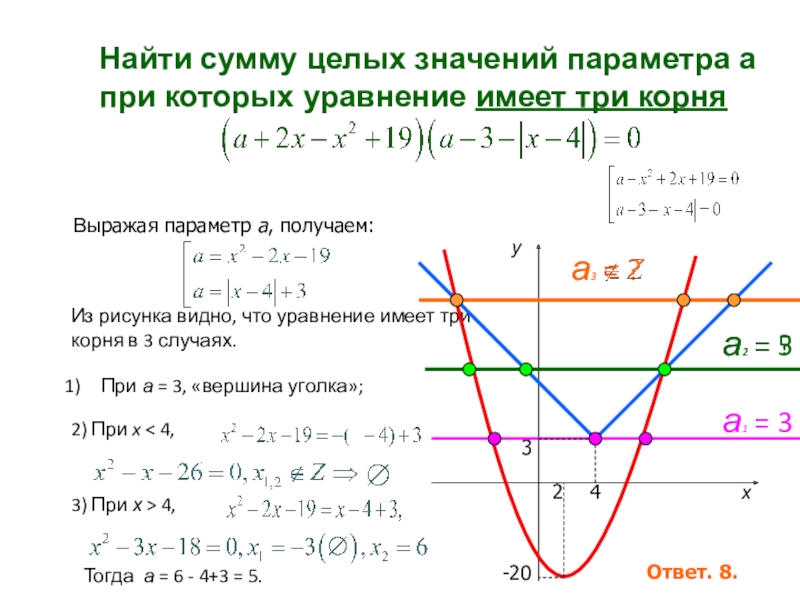
Слайд 34При а = 3, «вершина уголка»;
Найти сумму целых значений параметра
Исходное уравнение равносильно совокупности:
Выражая параметр а, получаем:
Из рисунка видно, что уравнение имеет три корня в 3 случаях.
3
4
-20
2
х
у
а1 = 3
а2 = ?
а3 = ?
Тогда а = 6 - 4+3 = 5.
Ответ. 8.
2) При x < 4,
3) При х > 4,
а2 = 5