- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Применение производной к исследованию функции
Содержание
- 1. Презентация Применение производной к исследованию функции
- 2. Отгадайте ключевое слово урока 1) С ее
- 3. Применение производной к исследованию функции
- 4. Применение производной к исследованию функцииОбобщение …; Отработка…с помощью производной;Закрепить … нахождения…;Применить ……для исследования функции Цели урока:
- 5. Лист достиженийФамилия, имя_______________________________________класс_____________
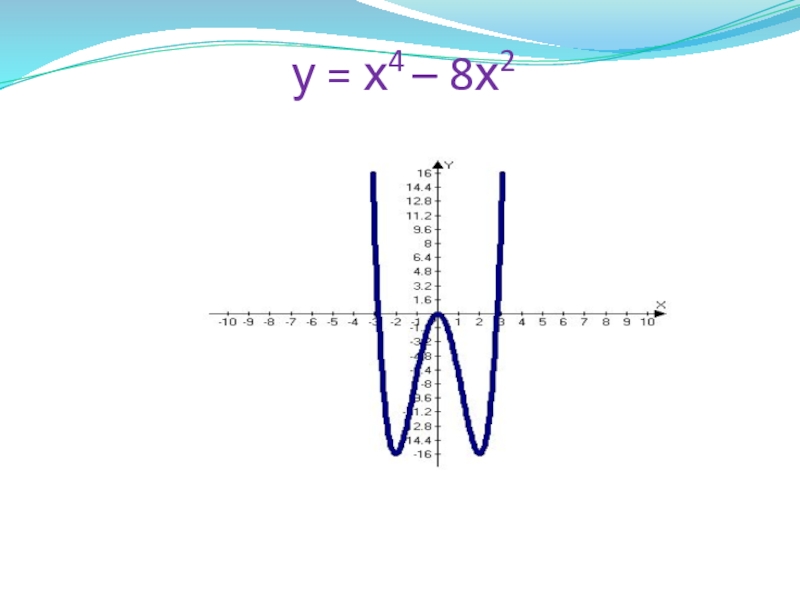
- 6. у = х4 – 8х2
- 7. Эпиграф нашего урока: «Знания имей отличные, исследуя функции различные».
- 8. Производная – одно из фундаментальных понятий математики.
- 9. Верно ли утверждение, определение?Функция возрастает на [-7;
- 10. Слайд 10
- 11. Заполни пропускиpk(kx+b)p-10
- 12. Найдите ошибку в вычислении производной:
- 13. Стационарными называют точки, в которых производная функциибольше 0равна 0больше 1меньше 0
- 14. f ' (х) < 0f ' (х)
- 15. Если при переходе через стационарную точку х0
- 16. Задан график y=f '(x) укажите: хуy=f '(x)
- 17. Задан график y=f '(x) проверьте! хуy=f '(x)
- 18. Найти промежутки возрастания и убывания функции
- 19. Задание ЕГЭНа рисунке изображен график функции у=f(x),
- 20. Возрастание, убывание функцииf’(x)>0функция возрастаетОтвет: 4 точкиНа рисунке
- 21. Возрастание, убывание функцииОтвет: 8 точек.На рисунке изображен
- 22. Производная функции в точке х0 равна 0
- 23. «Метод флюкций». Так Ньютон назвал свою
- 24. Найти точки экстремума и экстремум функции
- 25. План исследования функции:1. Нахождение области определения функции.2.
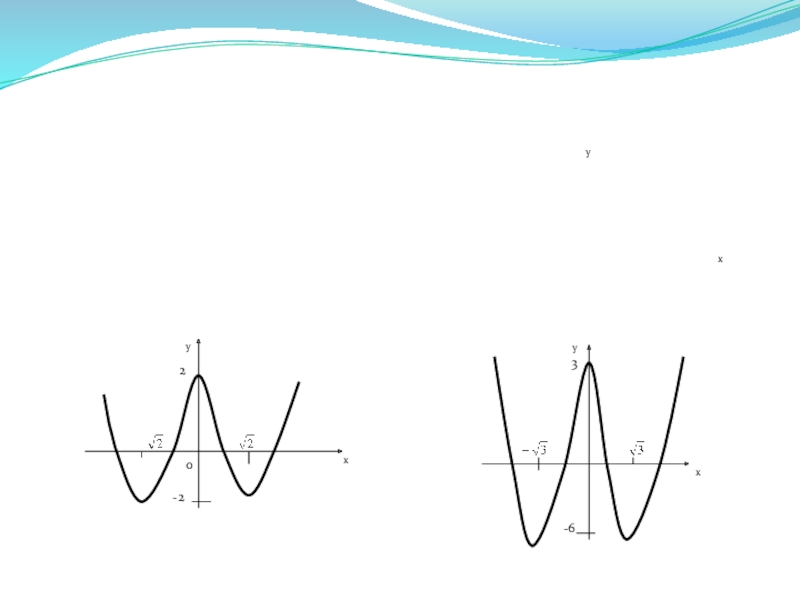
- 26. Построить график функции
- 27. З а д а н и я
- 28. Проверим свои работы.хххууу2-203-6
- 29. Подведение итогов
- 30. РефлексияНа уроке я работал
- 31. Домашнее задание
- 32. «Неважно сколько ученик знает сегодня, главное, чтобы
- 33. Всем спасибо за работу!
- 34. Слайд 34
Слайд 2Отгадайте ключевое слово урока
1) С ее появлением математика перешагнула из алгебры
2) Ньютон назвал ее «флюксией» и обозначал точкой;
3) Бывает первой, второй,… ;
4) Обозначается штрихом.
Слайд 4Применение производной к исследованию функции
Обобщение …;
Отработка…с помощью производной;
Закрепить … нахождения…;
Применить ……для
Цели урока:
Слайд 5Лист достижений
Фамилия, имя_______________________________________класс_____________
Слайд 8Производная – одно из фундаментальных понятий математики. Умение решать задачи с
Слайд 9Верно ли утверждение, определение?
Функция возрастает на [-7; 2) и (2; 8],
2. Производная функции в точке х0 равна 0, значит х0 - критическая точка. Верно ли?
3. Производная функции не существует в точке х0, значит х0 - критическая точка. Верно ли?
4. Критическая точка является точкой экстремума. Верно ли?
5. Точка экстремума является критической точкой. Верно ли?
-да, -нет
Слайд 14f ' (х) < 0
f ' (х) > 0
Функция убывает на
f '(х) = 0
Функция возрастает на этом промежутке
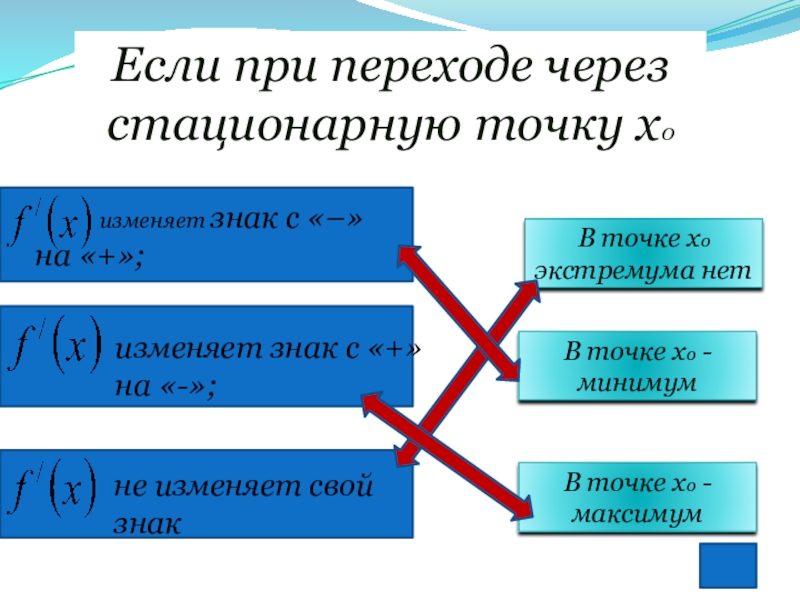
Слайд 15Если при переходе через стационарную точку х0
на «+»;
изменяет знак с «+»
на «-»;
не изменяет свой знак
В точке хо экстремума нет
В точке хо - минимум
В точке хо - максимум
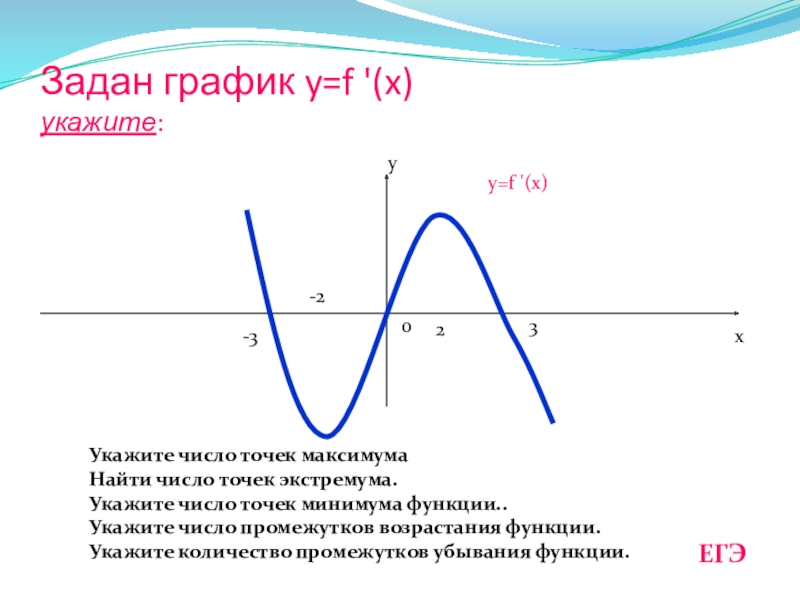
Слайд 16Задан график y=f '(x)
укажите:
х
у
y=f '(x)
-3
0
3
-2
2
Укажите число точек максимума
Найти число точек экстремума.
Укажите число точек минимума функции..
Укажите число промежутков возрастания функции.
Укажите количество промежутков убывания функции.
ЕГЭ
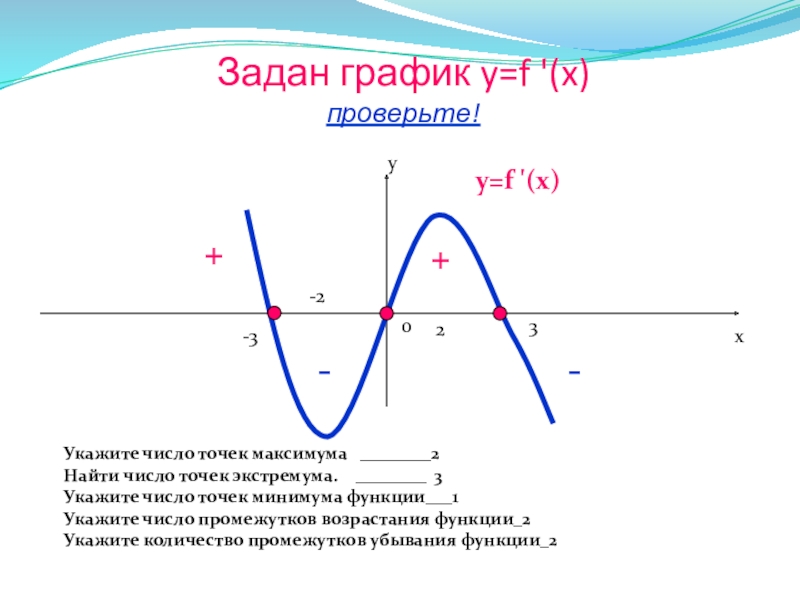
Слайд 17Задан график y=f '(x)
проверьте!
х
у
y=f '(x)
-3
0
3
-2
2
+
+
-
-
Укажите число точек максимума ________2
Найти число
Укажите число точек минимума функции___1
Укажите число промежутков возрастания функции_2
Укажите количество промежутков убывания функции_2
Слайд 19Задание ЕГЭ
На рисунке изображен график функции у=f(x), определенной на интервале (-6;8).
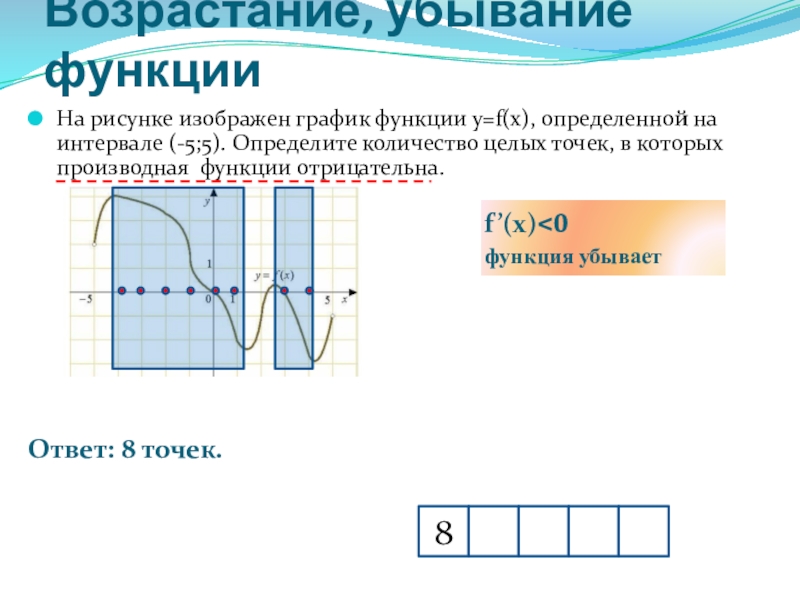
На рисунке изображен график функции у=f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.
На рисунке изображен график функции y = f (x),
определенной на интервале (-6; 8). Найдите количество точек, в
которых производная функции y = f (x) равна 0.
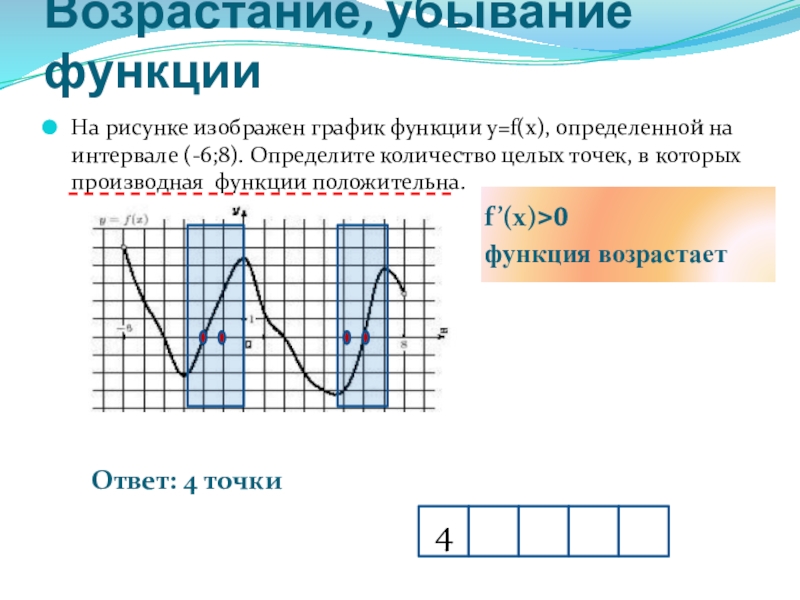
Слайд 20Возрастание, убывание функции
f’(x)>0
функция возрастает
Ответ: 4 точки
На рисунке изображен график функции у=f(x),
4
Слайд 21Возрастание, убывание функции
Ответ: 8 точек.
На рисунке изображен график функции у=f(x), определенной
f’(x)<0
функция убывает
8
Слайд 22Производная функции в точке х0 равна 0 тогда и только тогда,
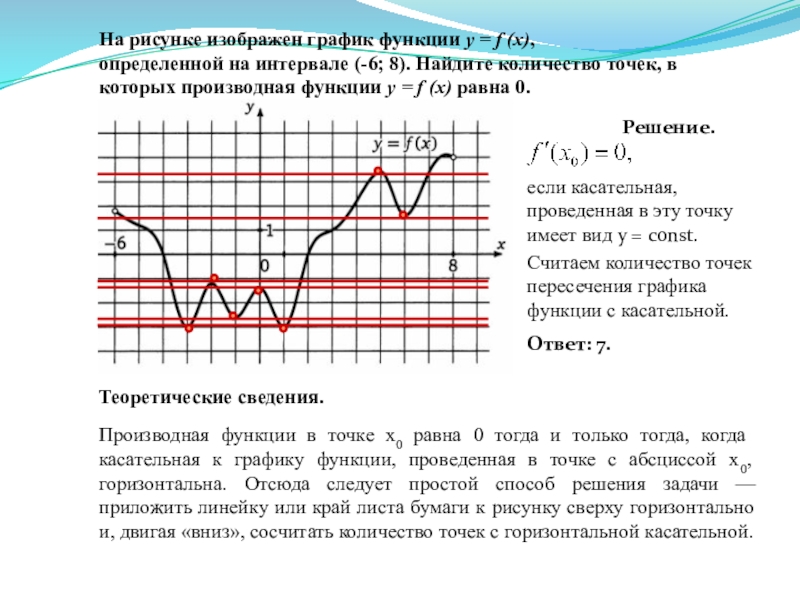
На рисунке изображен график функции y = f (x),
определенной на интервале (-6; 8). Найдите количество точек, в
которых производная функции y = f (x) равна 0.
Теоретические сведения.
Решение.
если касательная, проведенная в эту точку имеет вид у = const.
Считаем количество точек пересечения графика функции с касательной.
Ответ: 7.
Слайд 23 «Метод флюкций». Так Ньютон назвал свою работу,
посвященную основным понятиям
анализа. Функцию Ньютон назвал флюентой,
а производную – флюкцией. Обозначения Ньютона
для производных - х* (с точкой) и у* - сохранились
в физике до сих пор.
Производная – одно из фундаментальных понятий
математики. Оно возникло в XV11 веке. Независимо друг
от друга И.Ньютон и Г.Лейбниц разработали основные
элементы дифференциального исчисления.
Исторические сведения
Исчисление, созданное Ньютоном и Лейбницем, получило название дифференциального исчисления. С его помощью был решен целый ряд задач теоретической механики, физики и астрономии.
Слайд 25План исследования функции:
1. Нахождение области определения функции.
2. Определение стационарных точек.
3. Определение
4. Нахождение точек экстремума.
5. Составление сводной таблицы.
Построение графика функции.
Слайд 27З а д а н и я
Для функции у =
1) область определения;
2) производную;
3) критические точки;
4) Промежутки монотонности и экстремумы.
По результатам исследования постройте график.
л а б о р а т о р н а я р а б о т а
0
4
2
4
2
Слайд 30Рефлексия
На уроке я работал
Своей работой я доволен/недоволен
Урок для меня показался коротким/длинным
За урок я не устал/устал
Мое настроение стало лучше/стало хуже
Материал урока мне был понятен/непонятен






![Презентация Применение производной к исследованию функции Верно ли утверждение, определение?Функция возрастает на [-7; 2) и (2; 8], Верно ли утверждение, определение?Функция возрастает на [-7; 2) и (2; 8], значит, она возрастает на [-7; 8].](/img/thumbs/7c82f2eb0ab0555cf1da9e41fc77a8ac-800x.jpg)