Презентация, доклад по теме_Нахождение угла между прямой и плоскостью методом координат 2

проходящей через точки A1, E, F, где точка E – середина ребра C1D1, а точка F лежит на ребре DD1 так, что D1 F= 2DF

D1

B

D

C

B1

C1

A1

E

(1;0;0)

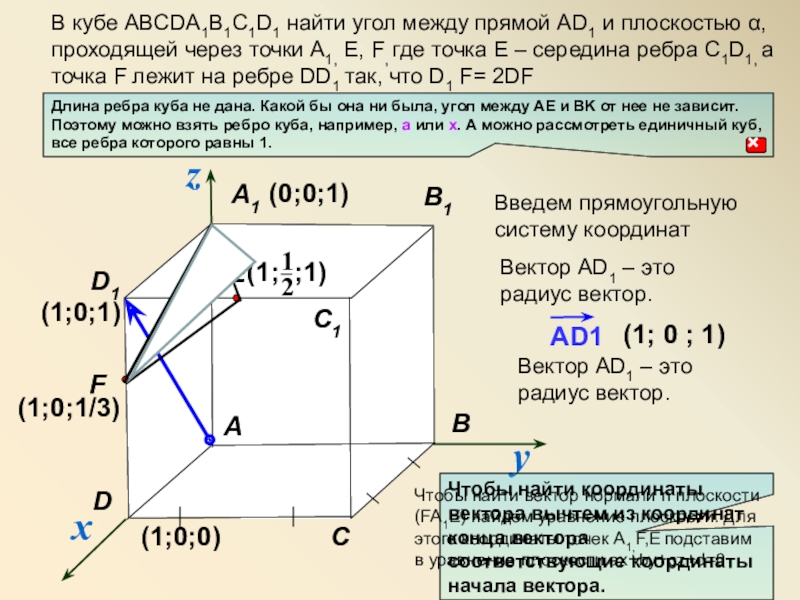
Введем прямоугольную систему координат

(1; 0 ; 1)

Вектор АD1 – это радиус вектор.

Чтобы найти координаты вектора вычтем из координат конца вектора соответствующие координаты начала вектора.

A

F

(1;0;1)

(0;0;1)

(1;0;1/3)

Вектор АD1 – это радиус вектор.

Чтобы найти вектор нормали n плоскости (FA1E) найдем уравнение плоскости. Для этого координаты точек A1,F,E подставим в уравнение плоскости ax+by+cz+d=0