- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме:Квадратные уравнения.Основные понятия
Содержание
- 1. Презентация по теме:Квадратные уравнения.Основные понятия
- 2. Многочлен ax2+bx+c называют квадратным трехчленома – первый
- 3. - неприведенное квадратное уравнение.- приведенное квадратное уравнение.Определение
- 4. Определение 4: Корнем квадратного уравнения ax2+bx+c=0 называют
- 5. Пример 1: Решить неполное квадратное уравнениеUROKIMATEMATIKI.RUИгорь Жаборовский © 2012
- 6. Решение неполных квадратных уравнений:1. Если уравнение имеет
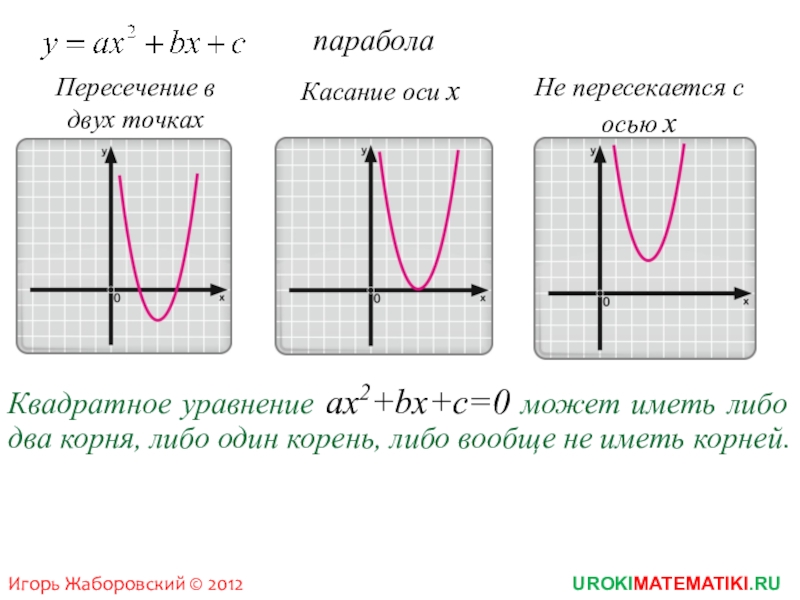
- 7. параболаПересечение в двух точкахКасание оси хНе пересекается
- 8. Пример 2: Решить уравнение VI способ: VII способ:UROKIMATEMATIKI.RUИгорь Жаборовский © 2012Решение:
Слайд 2Многочлен ax2+bx+c называют квадратным трехчленом
а – первый (старший) коэффициент
b – второй
с – свободный член
Определение 2: Квадратное уравнение называют приведенным, если старший коэффициент равен 1; квадратное уравнение называют непривиденным, если старший коэффициент отличен от 1.
UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
Слайд 3- неприведенное квадратное уравнение.
- приведенное квадратное уравнение.
Определение 3: Полное квадратное уравнение
Неполное квадратное уравнение – это квадратное уравнение, в котором присутствуют не все три слагаемых; это уравнение, у которого хотя бы один из коэффициентов b, c равен нулю.
UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
Слайд 4Определение 4: Корнем квадратного уравнения ax2+bx+c=0 называют всякое значение переменной х,
Корень квадратного уравнения ax2+bx+c=0 - это такое значение переменной х, подстановка которого в уравнение обращает уравнение в верное числовое равенство 0=0
Решить квадратное уравнение – значит найти все его корни или установить, что корней нет
UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
Слайд 6Решение неполных квадратных уравнений:
1. Если уравнение имеет вид ах2=0, то оно
2. Если уравнение имеет вид ах2+bx=0, то используется метод разложения на множители: х(ax+b)=0; значит, либо х=0, либо ax+b=0.
3. Если уравнение имеет вид ах2+с=0, то его преобразуют к виду ах2=-с, ; если - отрицательное число, уравнение
не имеет корней; если - положительное число, т.е.
уравнение x2=m имеет два корня:
UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
Слайд 7парабола
Пересечение в двух точках
Касание оси х
Не пересекается с осью х
Квадратное уравнение
UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
Слайд 8Пример 2: Решить уравнение
VI способ:
VII способ:
UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
Решение:
