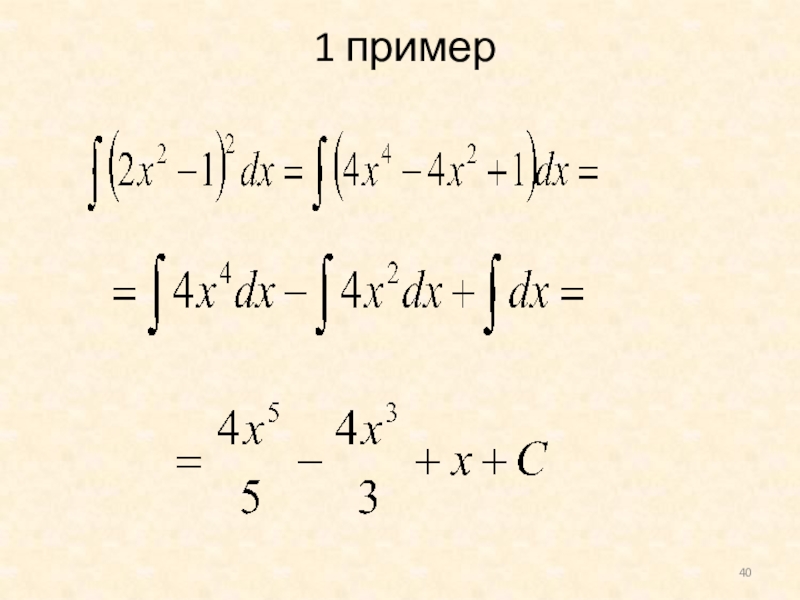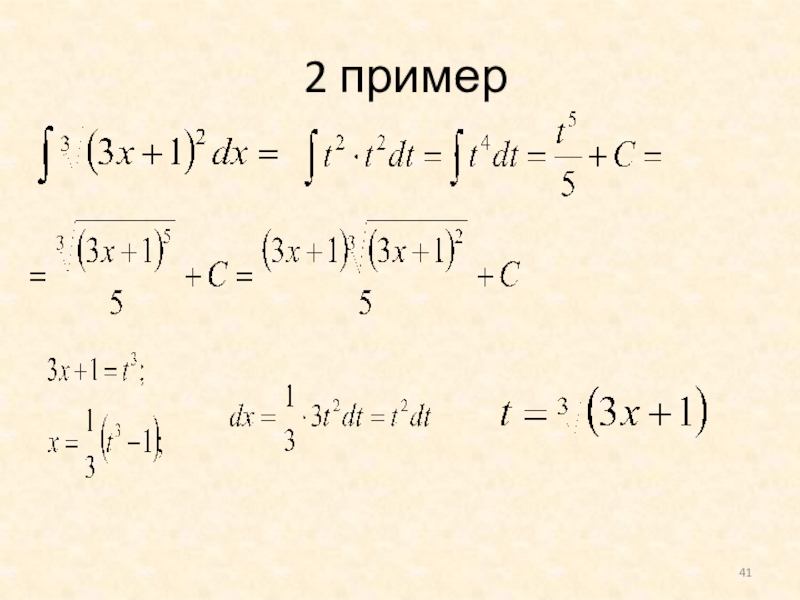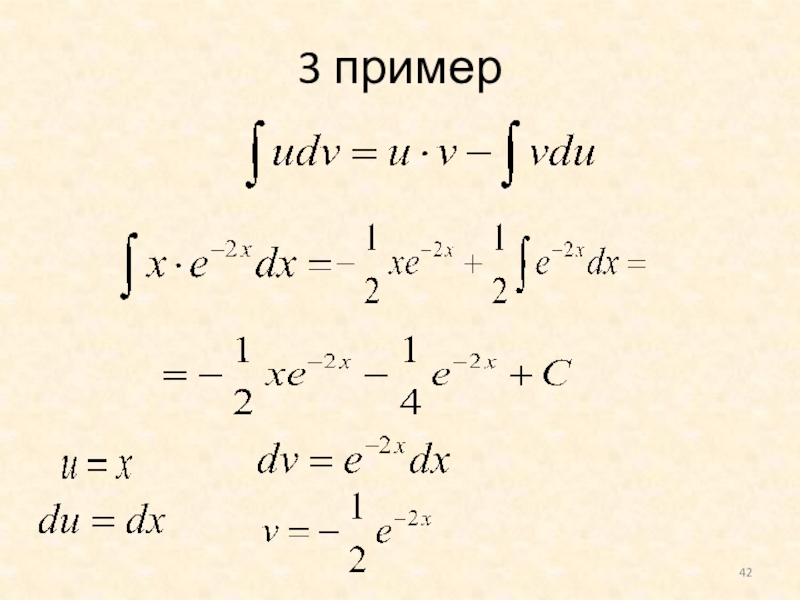Презентацию подготовил:
преподаватель ПРИХОДЬКО Ю.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Вычисление неопределенного интеграла
Содержание
- 1. Презентация по теме Вычисление неопределенного интеграла
- 2. ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛАТЕМА УРОКА
- 3. КОНФУЦИЙ – древнекитайский философ и мыслитель«Три пути
- 4. Цели урока :Обобщить и закрепить понятие неопределённого
- 5. Организационный этап.Из истории неопределённого интеграла.Фронтальный опрос по
- 6. Презентация по математикеИСТОРИЯ ВОЗНИКНОВЕНИЯ ИНТЕГРАЛАВыполнили: студенты гр. ДЛC-401Рожковская Cветлана, Репицкая ЛилияПроверил: преподавательПриходько Ю.В.
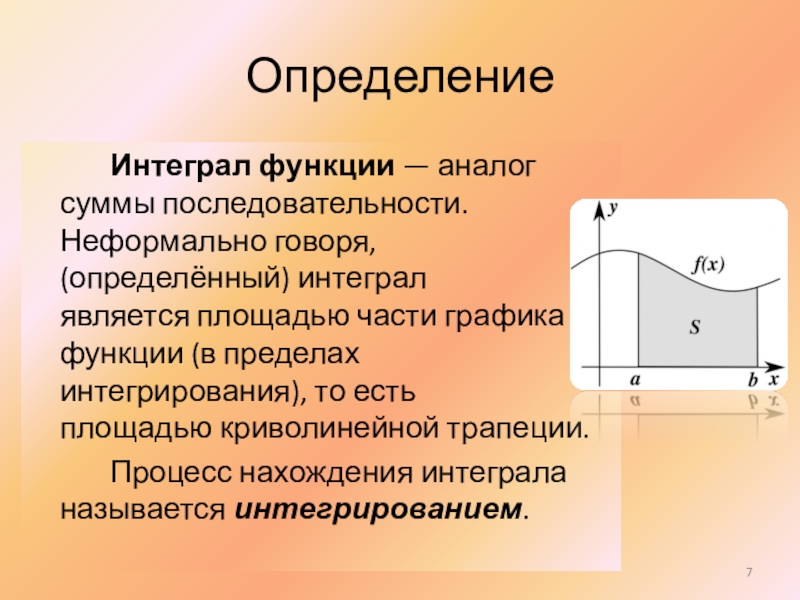
- 7. Определение Интеграл функции — аналог суммы последовательности. Неформально говоря,
- 8. Символ интеграла был введён Лейбницем (1675 г.).
- 9. Интеграл в древности Возникновение задач интегрального исчисления связано
- 10. Интеграл в древности Однако Архимед не выделил общего
- 11. История возникновения интеграла Труды Архимеда, впервые изданные в
- 12. История возникновения интеграла Например, криволинейную трапецию они представляли
- 13. История возникновения интеграла На такой кажущейся теперь по
- 14. История возникновения интеграла В XVII веке были сделаны
- 15. История возникновения интеграла Это сделали Ньютон и Лейбниц,
- 16. История возникновения интеграла Предстояло еще научиться находить первообразные
- 17. История возникновения интеграла Методы математического анализа активно развивались
- 18. История возникновения интеграла Строгое изложение теории интеграла появилось
- 19. История возникновения интеграла Ответы на многие вопросы, связанные
- 20. История возникновения интеграла Различные обобщения понятия интеграла уже
- 21. Фронтальный опрос по теории
- 22. Вопросы для повторенияВопросы3. Что называется интегрированием?4. Чем
- 23. Вопросы для повторенияВопросы5. Какая функция называется первообразной
- 24. Вопросы для повторенияВопросы6. Сформулируйте свойства неопределённого интеграла…Ответы-
- 25. Таблица неопределенных интегралов
- 26. Таблица неопределенных интегралов
- 27. МАТЕМАТИЧЕСКАЯ ЭСТАФЕТАИнструктаж: Работа в командах (по
- 28. Закрепление практических умений и навыковРешение типовых примеров по образцу
- 29. Примеры табличного интегрированияПримеры интегрирования методом подстановкиПример №1Пример №2Пример №3ТренингПример №4Пример №5Пример №6Пример №7
- 30. Пример №1Интеграл суммы выражений равен сумме интегралов этих выраженийПостоянный множитель можно вынести за знак интеграла
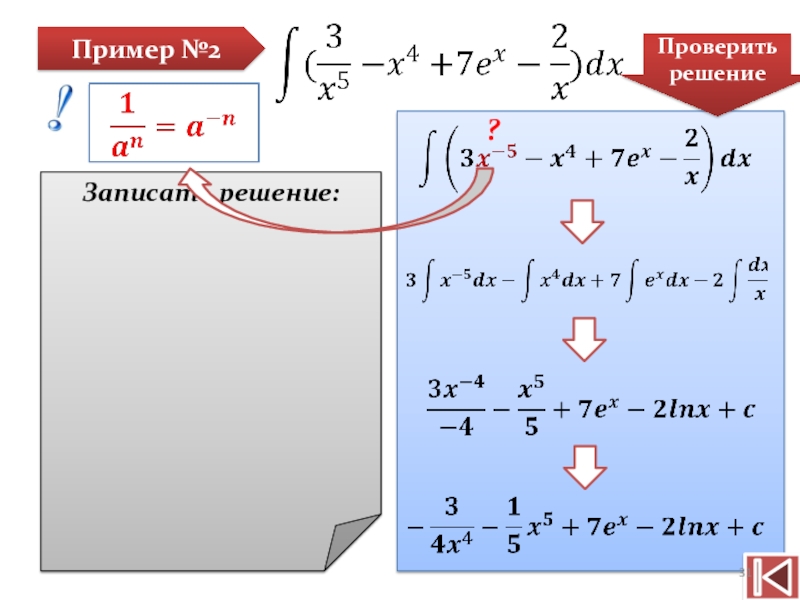
- 31. Пример №2Записать решение:Проверить решение?
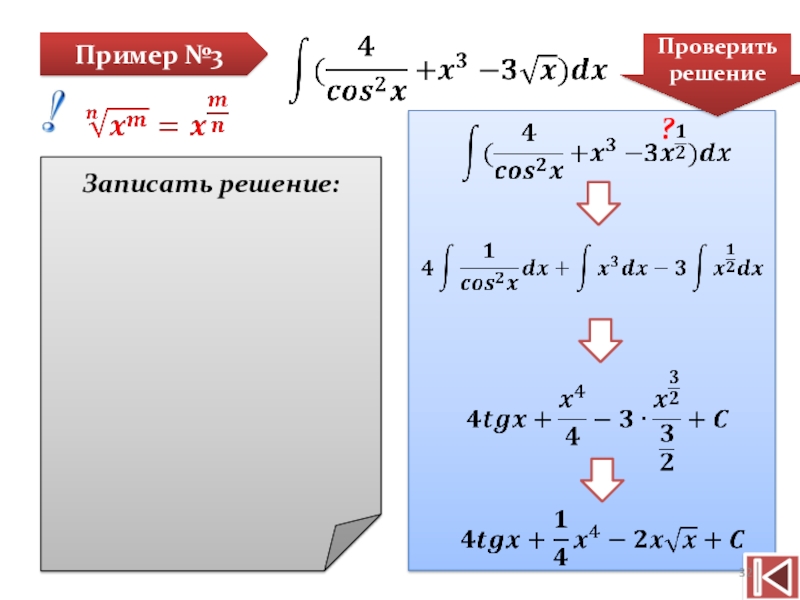
- 32. Пример №3Записать решение:Проверить решение?
- 33. Пример №4Все способы интегрирования имеют целью свести
- 34. Введем новую переменную и выразим дифференциалы:Пример №5Записать решение:Проверить решение
- 35. Введем новую переменную и найдем её дифференциалПример №6Записать решение:Проверить решение
- 36. Пример №7Записать решение:Проверить решение
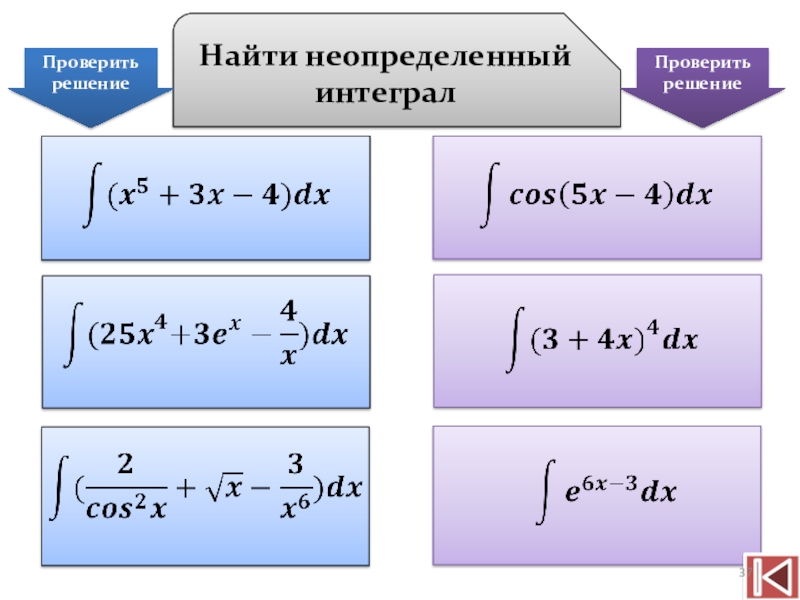
- 37. Найти неопределенный интегралПроверить решениеПроверить решение
- 38. Следует отметить, что для функции вида f(kx+b) можно применять упрощенную формулу
- 39. Решение типичных примеров1. Вычислить интеграл:2. Вычислить интеграл
- 40. 1 пример
- 41. 2 пример
- 42. 3 пример
- 43. Примем царственную позу, добиваясь хорошей
- 44. Применение практических умений и навыков«ВЫПОЛНЕНИЕ ПРАКТИЧЕСКОЙ РАБОТЫ»
- 45. ПРОВЕРКА УМЕНИЙ и НАВЫКОВ Самостоятельная
- 46. Информация по домашнему заданию:Повторить основные понятия
- 47. Ну кто придумал эту математику !У меня всё получилось!!!Надо решить ещё пару примеров.Рефлексия
- 48. Рефлексия деятельностиБлагодаря сегодняшнему уроку, я …Сегодняшний
- 49. ПОДВЕДЕНИЕ ИТОГОВ УРОКА“Музыка может возвышать или
- 50. Спасибоза активноеучастие на уроке!!!
ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛАТЕМА УРОКА
Слайд 1ПРЕЗЕНТАЦИЯ К УРОКУ МАТЕМАТИКИ ДЛЯ СТУДЕНТОВ 2 КУРСА
СПЕЦИАЛЬНОСТЬ СПО 40.02.01 «Право
и организация социального обеспечения»
Слайд 3КОНФУЦИЙ – древнекитайский философ и мыслитель
«Три пути ведут к знанию: путь
размышления – это путь самый благородный, путь подражания – это путь самый лёгкий и путь опыта – это путь самый горький».
Слайд 4Цели урока :
Обобщить и закрепить понятие неопределённого интеграла.
Повторить основные свойства интеграла.
Отработать
практические навыки вычисления неопределённого интеграла, используя различные приёмы.
Слайд 5Организационный этап.
Из истории неопределённого интеграла.
Фронтальный опрос по теории.
Работа по карточкам.
Математическая эстафета.
Закрепление
умений и навыков. Решение примеров по образцу.
Применение умений и навыков. Выполнение практической работы.
Проверка знаний. Самостоятельная работа.
Домашнее задание.
Рефлексия деятельности.
Подведение итогов урока.
Применение умений и навыков. Выполнение практической работы.
Проверка знаний. Самостоятельная работа.
Домашнее задание.
Рефлексия деятельности.
Подведение итогов урока.
План учебного занятия:
Слайд 6Презентация по математике
ИСТОРИЯ ВОЗНИКНОВЕНИЯ ИНТЕГРАЛА
Выполнили: студенты гр. ДЛC-401
Рожковская Cветлана, Репицкая Лилия
Проверил:
преподаватель
Приходько Ю.В.
Приходько Ю.В.
Слайд 7Определение
Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика
функции (в пределах интегрирования), то есть площадью криволинейной трапеции.
Процесс нахождения интеграла называется интегрированием.
Процесс нахождения интеграла называется интегрированием.
Слайд 8 Символ интеграла был введён Лейбницем (1675 г.). Этот знак является изменением
латинской буквы S (первой буквы слова сумма). Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integero, которое переводится, как приводить в прежнее состояние, восстанавливать.
Слайд 9Интеграл в древности
Возникновение задач интегрального исчисления связано с нахождением площадей и
объемов. Ряд задач такого рода был решен математиками древней Греции. Античная математика предвосхитила идеи интегрального исчисления в значительно большей степени, чем дифференциального исчисления. Большую роль при решении таких задач играл исчерпывающий метод, созданный Евдоксом Книдским (ок. 408 - ок. 355 до н. э.) и широко применявшийся Архимедом (ок. 287 - 212 до н. э.).
Слайд 10Интеграл в древности
Однако Архимед не выделил общего содержания интеграционных приемов и
понятий об интеграле, а тем более не создал алгоритма интегрального исчисления. Ученые Среднего и Ближнего Востока в IX - XV веках изучали и переводили труды Архимеда на общедоступный в их среде арабский язык, но существенно новых результатов в интегральном исчислении они не получили.
Деятельность европейских ученых в это время была еще более скромной. Лишь в XVI и XVII веках развитие естественных наук поставило перед математикой Европы ряд новых задач, в частности задачи на нахождение квадратур (задачи на вычисление площадей фигур), кубатур (задачи на вычисление объемов тел) и определение центров тяжести .
Слайд 11История возникновения интеграла
Труды Архимеда, впервые изданные в 1544 (на латинском и
греческом языках), стали привлекать широкое внимание, и их изучение явилось одним из важнейших отправных пунктов развития интегрального исчисления. Архимед предвосхитил многие идеи интегрального исчисления. Но потребовалось более полутора тысяч лет, прежде чем эти идеи нашли четкое выражение и были доведены до уровня исчисления.
Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Активно применялся и другой метод - метод неделимых, который также зародился в Древней Греции.
Слайд 12История возникновения интеграла
Например, криволинейную трапецию они представляли себе составленной из вертикальных
отрезков длиной f(x) , которым тем не менее приписывали площадь, равную бесконечно малой величине f(x)dx. В соответствии с таким пониманием искомая площадь считалась равной сумме S бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме - нули, но нули особого рода, которые сложенные в бесконечном числе, дают вполне определенную положительную сумму.
Слайд 13История возникновения интеграла
На такой кажущейся теперь по меньшей мере сомнительной основе
И. Кеплер (1571 - 1630 гг.) в своих сочинениях "Новая астрономия" (1609 г.) и "Стереометрия винных бочек" (1615 г.) правильно вычислил ряд площадей (например площадь фигуры, ограниченной эллипсом) и объемов (тело резалось на бесконечно тонкие пластинки).
Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598 - 1647 годы) и Э. Торричелли (1608 -1647 годы).
Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598 - 1647 годы) и Э. Торричелли (1608 -1647 годы).
Слайд 14История возникновения интеграла
В XVII веке были сделаны многие открытия, относящиеся к
интегральному исчислению.
Однако при всей значимости результатов, полученных математиками XVII столетия, исчисления еще не было. Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно точный алгоритм.
Однако при всей значимости результатов, полученных математиками XVII столетия, исчисления еще не было. Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно точный алгоритм.
Слайд 15История возникновения интеграла
Это сделали Ньютон и Лейбниц, открывшие независимо друг от
друга факт, известный вам под названием формулы Ньютона - Лейбница. Тем самым окончательно оформился общий метод.
Слайд 16История возникновения интеграла
Предстояло еще научиться находить первообразные многих функций, дать логические
основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.
Слайд 17История возникновения интеграла
Методы математического анализа активно развивались в следующем столетии (в
первую очередь следует назвать имена Л. Эйлера, завершившего систематическое исследование интегрирования элементарных функций, и И. Бернулли). В развитии интегрального исчисления приняли участие русские математики М. В. Остроградский (1801 - 1862 гг.), В. Я. Буняковский (1804 - 1889 гг.), П. Л. Чебышев (1821 - 1894 гг.). Принципиальное значение имели, в частности, результаты Чебышева, доказавшего, что существуют интегралы, не выразимые через элементарные функции.
Слайд 18История возникновения интеграла
Строгое изложение теории интеграла появилось только в прошлом веке,
Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков, немецкого ученого Б. Римана (1826 - 1866 гг.), французского математика Г. Дарбу (1842 - 1917).
Слайд 19История возникновения интеграла
Ответы на многие вопросы, связанные с существованием площадей и
объемов фигур, были получены с созданием К. Жорданом (1826 - 1922 гг.) теории меры.
Слайд 20История возникновения интеграла
Различные обобщения понятия интеграла уже в начале нашего столетия
были предложены французскими математиками А. Лебегом (1875 - 1941 гг.) и А. Данжуа (1884 - 1974) советским математиком А. Я. Хинчиным (1894 -1959 гг.)
Слайд 21Фронтальный опрос по теории
Вопросы
1. Дать определение неопределённого интеграла.
2. Какие способы вычисления неопределённого интеграла вы знаете?
Ответы
1. Совокупность всех первообразных F(x)+С
для функции f(x).
2. 3 способа: способ непосредственного интегрирования, способ замены, способ интегрирования по частям.
Слайд 22Вопросы для повторения
Вопросы
3. Что называется интегрированием?
4. Чем отличаются друг от друга
различные первообразные для данной функции f(x)?
Ответы
3.Операция нахождения неопределённого интеграла от данной функции.
4. Постоянной С.
Слайд 23Вопросы для повторения
Вопросы
5. Какая функция называется первообразной для данной функции f(x)?
Ответы
5.
Функция F(x) называется первообразной для функции f(x) на интервале (a;b), если для всех х:
Слайд 24Вопросы для повторения
Вопросы
6. Сформулируйте свойства неопределённого интеграла…
Ответы
- Постоянный множитель можно выносить
за знак интеграла;
Интеграл суммы равен сумме интегралов слагаемых;
Производная неопределённого интеграла равна подынтегральной функции;
Дифференциал неопределённого интеграла равен подынтегральному выражению.
Интеграл суммы равен сумме интегралов слагаемых;
Производная неопределённого интеграла равна подынтегральной функции;
Дифференциал неопределённого интеграла равен подынтегральному выражению.
Слайд 27 МАТЕМАТИЧЕСКАЯ ЭСТАФЕТА
Инструктаж: Работа в командах (по рядам). На последней парте
каждого ряда находится листок с 10 заданиями (по два примера на каждую парту). Первая пара учащихся, выполнив любые два задания, передает листок впереди сидящим. Работа считается оконченной, когда учитель получается листок с правильно выполненными 10 заданиями. Вы можете решить не только свои задания, но и проверить правильность решения членов своей команды. Побеждает та команда, которая правильно и раньше всех решит все задания.
Слайд 29Примеры
табличного интегрирования
Примеры интегрирования методом подстановки
Пример №1
Пример №2
Пример №3
Тренинг
Пример №4
Пример №5
Пример
№6
Пример №7
Слайд 30Пример №1
Интеграл суммы выражений равен сумме интегралов этих выражений
Постоянный множитель можно
вынести за знак интеграла
Слайд 33Пример №4
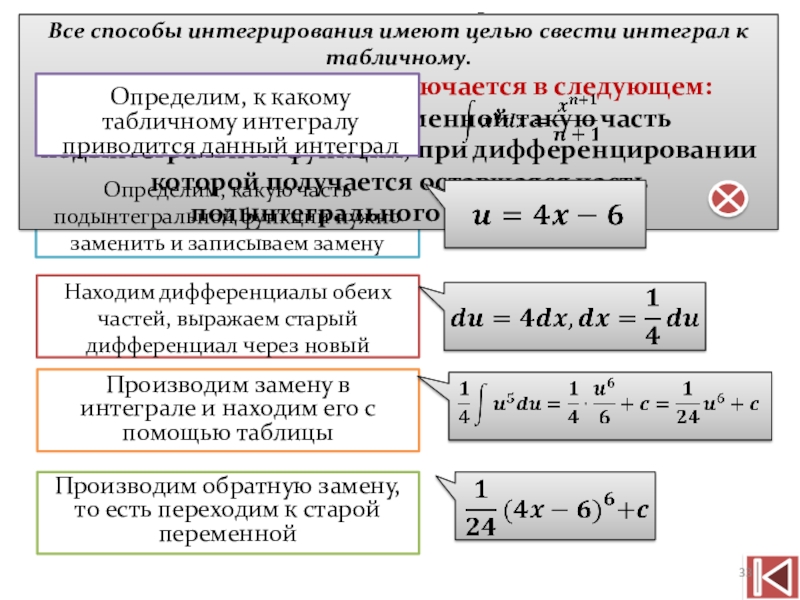
Все способы интегрирования имеют целью свести интеграл к табличному.
Способ подстановки
заключается в следующем:
заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения.
заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения.
Определим, к какому табличному интегралу приводится данный интеграл
Определим, какую часть подынтегральной функции нужно заменить и записываем замену
Находим дифференциалы обеих частей, выражаем старый дифференциал через новый
Производим замену в интеграле и находим его с помощью таблицы
Производим обратную замену, то есть переходим к старой переменной
Слайд 39Решение типичных примеров
1. Вычислить интеграл:
2. Вычислить интеграл методом подстановки:
3.
Вычислить интеграл методом интегрирования по частям:
Слайд 43 Примем царственную позу, добиваясь хорошей осанки. Три раза вдохнём.
Массажируем кончики пальцев каждой руки. Поставьте указательный палец на точку между бровями и массажируйте три раза. Закрыть веки, массировать их с помощью легких круговых движений пальца.
ФИЗКУЛЬТМИНУТКА
Слайд 45 ПРОВЕРКА УМЕНИЙ и НАВЫКОВ
Самостоятельная работа по теме: «Вычисление
неопределённого интеграла»
КРИТЕРИЙ ОЦЕНОК:
ОЦЕНКА «5» – за правильное решение всех 3-х примеров;
ОЦЕНКА «4» – за правильное решение 2-х примеров;
ОЦЕНКА «3» – за правильное решение 1-го примера.
КРИТЕРИЙ ОЦЕНОК:
ОЦЕНКА «5» – за правильное решение всех 3-х примеров;
ОЦЕНКА «4» – за правильное решение 2-х примеров;
ОЦЕНКА «3» – за правильное решение 1-го примера.
Слайд 46 Информация по домашнему заданию:
Повторить основные понятия и свойства по теме
«Неопределённый интеграл».
Составить кроссворд (ребус) по теме «Неопределённый интеграл».
Выполнить решение примеров по карточкам.
Составить кроссворд (ребус) по теме «Неопределённый интеграл».
Выполнить решение примеров по карточкам.
Слайд 47Ну кто придумал эту математику !
У меня всё получилось!!!
Надо решить ещё
пару примеров.
Рефлексия
Слайд 48 Рефлексия деятельности
Благодаря сегодняшнему уроку, я …
Сегодняшний урок помог мне …
Сегодня
на уроке мне запомнилось …
Сегодня на уроке мне больше всего понравилось …
После сегодняшнего урока мне захотелось …
Сегодня на уроке я узнал(а) …
После сегодняшнего урока я буду знать …
После сегодняшнего урока я хочу сказать …
Сегодня на уроке я научился …
Сегодняшний урок дал мне …
Сегодня на уроке мне больше всего понравилось …
После сегодняшнего урока мне захотелось …
Сегодня на уроке я узнал(а) …
После сегодняшнего урока я буду знать …
После сегодняшнего урока я хочу сказать …
Сегодня на уроке я научился …
Сегодняшний урок дал мне …
Слайд 49 ПОДВЕДЕНИЕ ИТОГОВ УРОКА
“Музыка может возвышать или умиротворять душу,
Живопись – радовать
глаз,
Поэзия - пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать
материальную сторону жизни людей,
а математика способна достичь всех этих целей”.
американский математик Морис Клайн.
Поэзия - пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать
материальную сторону жизни людей,
а математика способна достичь всех этих целей”.
американский математик Морис Клайн.
