- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
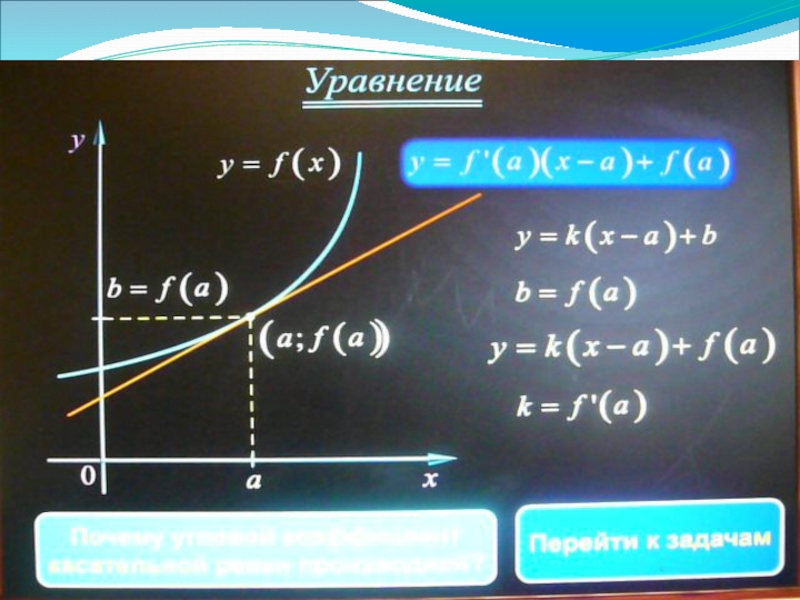
Презентация, доклад по теме Уравнение касательной
Содержание
- 1. Презентация по теме Уравнение касательной
- 2. Девиз урока:Плохих идей не бываетМыслите творческиРискуйте Не критикуйте
- 3. Найти производную функции1.Y=5
- 4. Согласны ли вы с утверждением:Касательная – это прямая, имеющая с данной кривой одну общую точку
- 5. одну общую точку М (1; 1) однако
- 6. Прямая х = π не является касательной
- 7. Касательная –это предельное положение секущей
- 8. y=kx+bk- угловой коэффициентk = tgαf´(x) = tgα
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Понятие "производная" возникло в связис необходимостью решения
- 13. Потренируемся:
- 14. Слайд 14
- 15. Слайд 15
- 16. Подведение итоговЧто называется касательной
- 17. СПАСИБО ЗА УРОК!
Слайд 4Согласны ли вы с утверждением:
Касательная – это прямая, имеющая с данной
Слайд 5
одну общую точку М (1; 1) однако не является касательной к
Прямая же у = 2х – 1, проходящая через ту же точку,является касательной к даной параболе.
Прямая х=1 имеет с параболой У=
Слайд 6Прямая х = π не является касательной к графику у =
Слайд 11 Алгоритм
1.
2. Вычислим f(а)
3. Найдем f´(x) и вычислим f´(а)
4. Подставим найденные значения в общее уравнение касательной.
5. y = f(a) + f / (a) · (x - a)
Слайд 12Понятие "производная" возникло в связи
с необходимостью решения ряда задач
физики, механики
Честь открытия
основных законов
математического
анализа принадлежит
английскому ученому
Ньютону и немецкому
математику Лейбницу
Лейбниц рассматривал
задачу о проведении
касательной к произвольной
кривой.
Слайд 13 Потренируемся:
а = -1
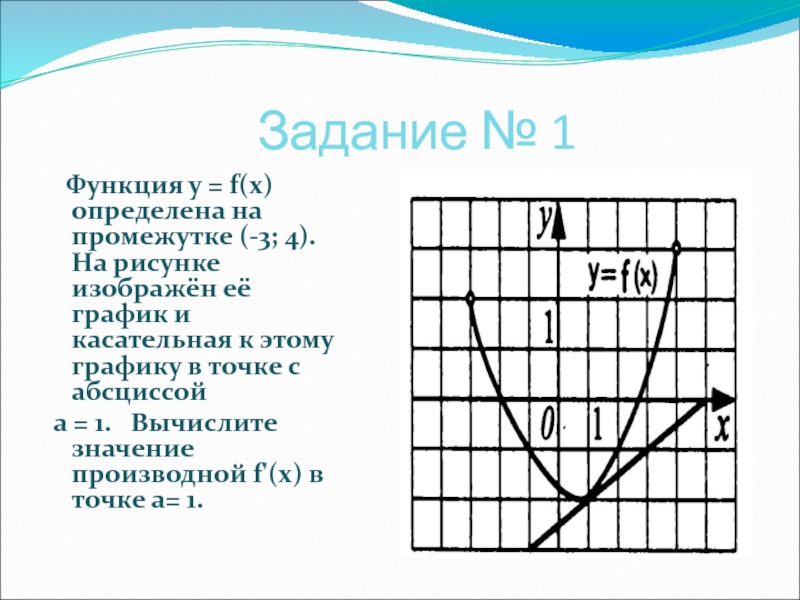
Слайд 14 Задание №
Функция у = f(x) определена на промежутке (-3; 4). На рисунке изображён её график и касательная к этому графику в точке с абсциссой
а = 1. Вычислите значение производной f'(x) в точке а= 1.
Слайд 15 Задание
Функция у = f(x) определена на промежутке (-3;4). На рисунке изображён её график и касательная к этому графику в точке с абсциссой а = -2. Вычислите значение производной f'(x) в точке а = -2.
Слайд 16 Подведение итогов
Что называется касательной к графику функции в
В чём заключается геометрический смысл производной?
Сформулируйте алгоритм нахождения уравнения касательной в точке?