- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Тригонометрические функции
Содержание
- 1. Презентация по теме Тригонометрические функции
- 2. ТригонометрияТригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при
- 3. Основные свойства функции.1. Область определения.2. Область значений.3.
- 4. Функция y = sin xГрафик функции
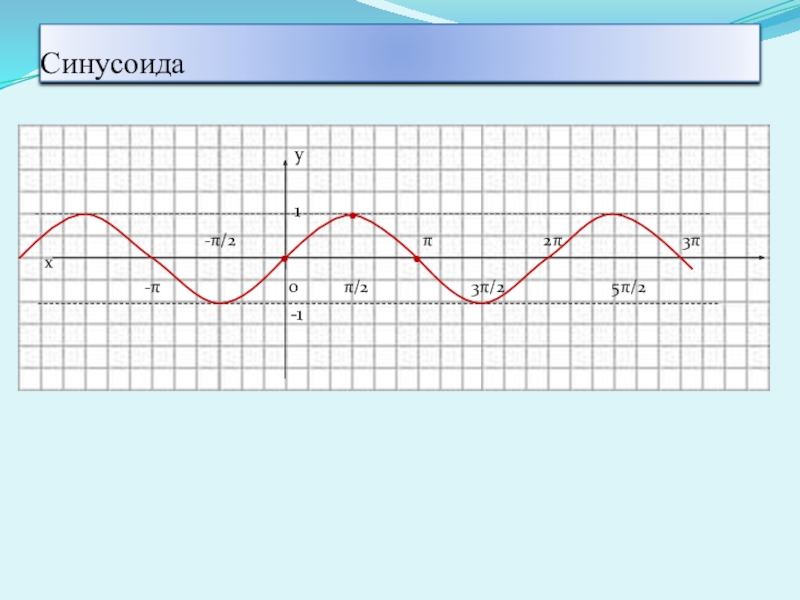
- 5. Синусоида
- 6. Функция y = cosxГрафик функции
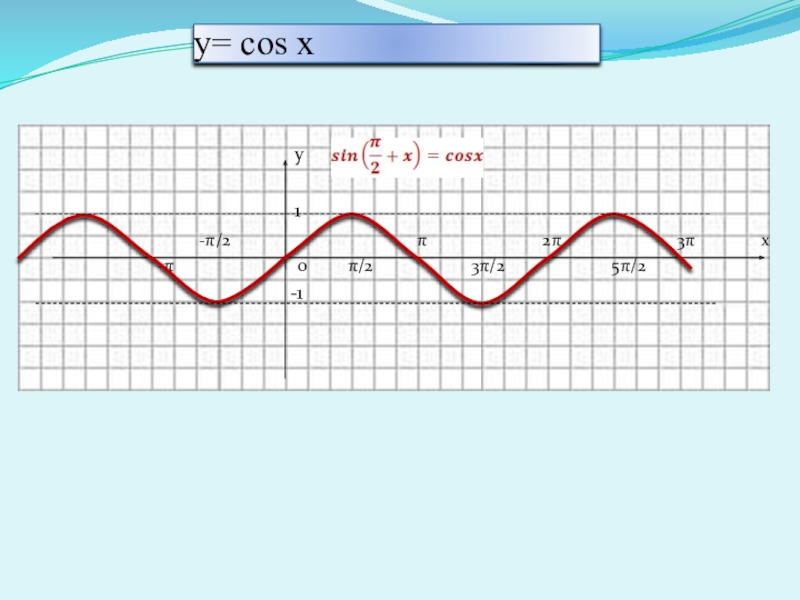
- 7. y= cos x
- 8. Функция y = tg xГрафик функции
- 9. Функция y = ctg xГрафик функции
- 10. Исследование тригонометрических функций на четность y
- 11. Монотонность тригонометрических функций. y = cos x
- 12. Монотонность тригонометрических функций. y = sin x.
- 13. Определение промежутков знакопостоянства тригонометрических функций.y = tg
- 14. Определение промежутков знакопостоянства тригонометрических функций. y =
ТригонометрияТригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение
Слайд 2Тригонометрия
Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости
сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
Слайд 3Основные свойства функции.
1. Область определения.
2. Область значений.
3. Периодичность.
4. Четность, нечетность.
5. Нули.
6.
Промежутки монотонности.
7. Промежутки знакопостоянства.
8. Наибольшее и наименьшее значения.
7. Промежутки знакопостоянства.
8. Наибольшее и наименьшее значения.
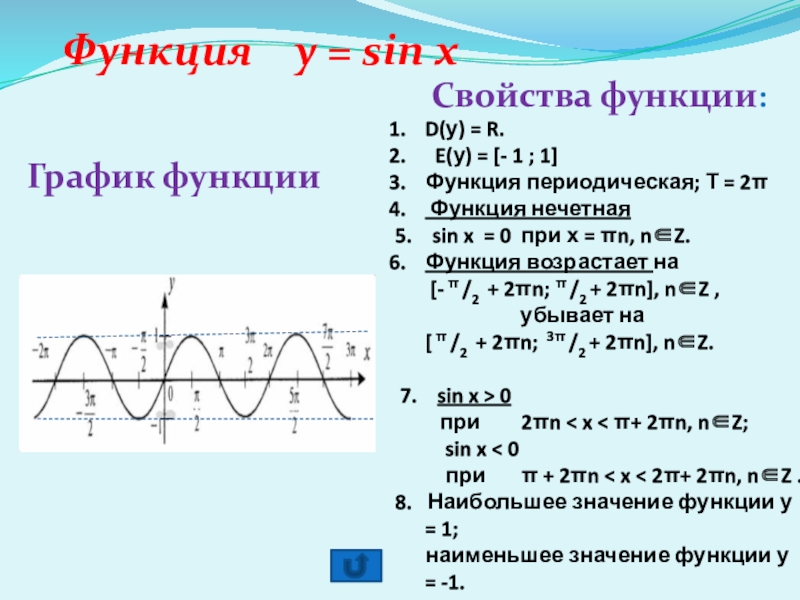
Слайд 4Функция y = sin x
График функции
Свойства функции:
D(у) =
R.
E(у) = [- 1 ; 1]
Функция периодическая; Т = 2π
Функция нечетная
5. sin x = 0 при х = πn, nZ.
Функция возрастает на
[- π /2 + 2πn; π /2 + 2πn], nZ ,
убывает на
[ π /2 + 2πn; 3π /2 + 2πn], nZ.
7. sin x > 0
при 2πn < x < π+ 2πn, nZ;
sin x < 0
при π + 2πn < x < 2π+ 2πn, nZ .
8. Наибольшее значение функции у = 1;
наименьшее значение функции у = -1.
E(у) = [- 1 ; 1]
Функция периодическая; Т = 2π
Функция нечетная
5. sin x = 0 при х = πn, nZ.
Функция возрастает на
[- π /2 + 2πn; π /2 + 2πn], nZ ,
убывает на
[ π /2 + 2πn; 3π /2 + 2πn], nZ.
7. sin x > 0
при 2πn < x < π+ 2πn, nZ;
sin x < 0
при π + 2πn < x < 2π+ 2πn, nZ .
8. Наибольшее значение функции у = 1;
наименьшее значение функции у = -1.
Слайд 6Функция y = cosx
График функции
Свойства функции:
D(у) = R.
E(у) = [- 1 ; 1]
Функция периодическая; Т = 2π
Функция четная.
5. cos x = 0 при х = π /2 + πn, nZ , nZ.
6. Функция возрастает на
[ π+ 2πn; 2π+ 2πn], nZ,
убывает на
[ 2πn; π+ 2πn], nZ.
7. cos x > 0
при - π /2 + 2πn < x < π /2 + 2πn, nZ;
cos x < 0
при π /2 + 2πn < x < 3π /2 + 2πn, nZ
8. Наибольшее значение функции у = 1;
наименьшее значение функции у = -1.
Функция периодическая; Т = 2π
Функция четная.
5. cos x = 0 при х = π /2 + πn, nZ , nZ.
6. Функция возрастает на
[ π+ 2πn; 2π+ 2πn], nZ,
убывает на
[ 2πn; π+ 2πn], nZ.
7. cos x > 0
при - π /2 + 2πn < x < π /2 + 2πn, nZ;
cos x < 0
при π /2 + 2πn < x < 3π /2 + 2πn, nZ
8. Наибольшее значение функции у = 1;
наименьшее значение функции у = -1.
Слайд 8Функция y = tg x
График функции
Свойства функции:
D(y) =
(- π /2 + πn; π /2 + πn) ; nZ.
E(у) = R.
Функция периодическая; T = π.
Функция нечетная.
5. tg x = 0 при х = πn, nZ.
Функция возрастает на
(- π /2 + πn; π /2 + πn), nZ
tg x > 0
при πn < x < π /2 + πn, nZ;
tg x < 0
при - π /2 + πn < x < πn, nZ .
Функция не достигает наибольшего и наименьшего значений.
Прямые π /2 + πn , nZ, являются асимптотами графика функции.
E(у) = R.
Функция периодическая; T = π.
Функция нечетная.
5. tg x = 0 при х = πn, nZ.
Функция возрастает на
(- π /2 + πn; π /2 + πn), nZ
tg x > 0
при πn < x < π /2 + πn, nZ;
tg x < 0
при - π /2 + πn < x < πn, nZ .
Функция не достигает наибольшего и наименьшего значений.
Прямые π /2 + πn , nZ, являются асимптотами графика функции.
Слайд 9Функция y = ctg x
График функции
Свойства функции:
D(у) =
( πn; π+ πn ) , nZ.
E(у) = R
Функция периодическая; Т = π.
4. Функция нечетная.
ctg x = 0 при х = π /2 + πn, nZ .
Функция убывает на
(πn; π+ πn), nZ .
ctg x > 0
при πn < x < π /2 + πn, nZ;
ctg x < 0
при π /2 + πn < x < π + πn, nZ.
Функция не достигает наибольшего и наименьшего значений.
Прямые πn, nZ, являются асимптотами графика функции.
E(у) = R
Функция периодическая; Т = π.
4. Функция нечетная.
ctg x = 0 при х = π /2 + πn, nZ .
Функция убывает на
(πn; π+ πn), nZ .
ctg x > 0
при πn < x < π /2 + πn, nZ;
ctg x < 0
при π /2 + πn < x < π + πn, nZ.
Функция не достигает наибольшего и наименьшего значений.
Прямые πn, nZ, являются асимптотами графика функции.
Слайд 10Исследование тригонометрических функций
на четность
y = sin x. Функция нечетная.
1)
(-x) D(y).
2) y(-x) = sin (-x) = - sin x = - y(x).
y = cos x . Функция четная.
1) (-x) D(y).
2) y(-x) = cos (-x) = cos x = y(x).
y= tg x. Функция нечетная.
1) (-x) D(y).
2) y(-x) = tg (-x) = - tg x = - y(x).
y= ctg x. Функция нечетная.
1) (-x) D(y).
2) y(-x) = ctg (-x) = - ctg x = - y(x).
2) y(-x) = sin (-x) = - sin x = - y(x).
y = cos x . Функция четная.
1) (-x) D(y).
2) y(-x) = cos (-x) = cos x = y(x).
y= tg x. Функция нечетная.
1) (-x) D(y).
2) y(-x) = tg (-x) = - tg x = - y(x).
y= ctg x. Функция нечетная.
1) (-x) D(y).
2) y(-x) = ctg (-x) = - ctg x = - y(x).
Слайд 11Монотонность тригонометрических функций.
y = cos x .
Функция возрастает на
[ π+ 2πn; 2π+ 2πn], nZ,
убывает на [ 2πn; π+ 2πn], nZ.
Доказательство. 1) При повороте
точки (1; 0) вокруг начала координат против
часовой стрелки на угол от 0 до π π (1; 0) 0
абсцисса точки, т.е cos x, -1 1
уменьшается от 1 до -1. Поэтому если
0 ≤ Х1 < Х2 ≤ π то cos Х1> cos Х2.
Это означает, что функция y = cos x убывает на [ 0; π].
2) Функция y = cos x возрастает на [ -π; 0], т.к. она убывает на
[0; π] и является четной.
3) Т.к. функция периодическая с периодом Т = 2π, то она возрастает на [ π+ 2πn; 2π+ 2πn], nZ, убывает на [ 2πn; π+ 2πn], nZ.
убывает на [ 2πn; π+ 2πn], nZ.
Доказательство. 1) При повороте
точки (1; 0) вокруг начала координат против
часовой стрелки на угол от 0 до π π (1; 0) 0
абсцисса точки, т.е cos x, -1 1
уменьшается от 1 до -1. Поэтому если
0 ≤ Х1 < Х2 ≤ π то cos Х1> cos Х2.
Это означает, что функция y = cos x убывает на [ 0; π].
2) Функция y = cos x возрастает на [ -π; 0], т.к. она убывает на
[0; π] и является четной.
3) Т.к. функция периодическая с периодом Т = 2π, то она возрастает на [ π+ 2πn; 2π+ 2πn], nZ, убывает на [ 2πn; π+ 2πn], nZ.
Слайд 12Монотонность тригонометрических функций.
y = sin x.
Функция возрастает на
[- π /2 + 2πn; π /2 + 2πn], nZ ,
убывает на [ π /2 + 2πn; 3π /2 + 2πn], nZ.
Доказательство. 1) При повороте 1 π /2
точки вокруг начала координат против
часовой стрелки на угол от - π /2
до π /2 ордината точки, т.е sin x,
увеличивается от -1 до 1. Поэтому если
- π /2 ≤ Х1 < Х2 ≤ π /2 , то sin Х1< sin Х2. -1 - π /2
Это означает, что функция y = sin x возрастает на
[- π /2 ; π /2 ]. 2) Т.к. функция периодическая с периодом Т = 2π, то она возрастает на [- π /2 + 2πn; π /2 + 2πn], nZ .
Убывание функции на [ π /2 + 2πn; 3π /2 + 2πn], nZ,
доказывается аналогично.
убывает на [ π /2 + 2πn; 3π /2 + 2πn], nZ.
Доказательство. 1) При повороте 1 π /2
точки вокруг начала координат против
часовой стрелки на угол от - π /2
до π /2 ордината точки, т.е sin x,
увеличивается от -1 до 1. Поэтому если
- π /2 ≤ Х1 < Х2 ≤ π /2 , то sin Х1< sin Х2. -1 - π /2
Это означает, что функция y = sin x возрастает на
[- π /2 ; π /2 ]. 2) Т.к. функция периодическая с периодом Т = 2π, то она возрастает на [- π /2 + 2πn; π /2 + 2πn], nZ .
Убывание функции на [ π /2 + 2πn; 3π /2 + 2πn], nZ,
доказывается аналогично.
Слайд 13Определение промежутков знакопостоянства
тригонометрических функций.
y = tg x
tg x > 0 при πn < x < π /2 + πn, nZ; — +
tg x < 0 при - π /2 + πn < x < πn, nZ .
+ —
y = ctg x
ctg x > 0 при πn < x < π /2 + πn, nZ;
ctg x < 0 при π /2 + πn < x < π + πn, nZ.
Слайд 14Определение промежутков знакопостоянства
тригонометрических функций.
y = sin x .
+ +
sin x > 0 при 2πn < x < π+ 2πn, nZ;
sin x < 0 при π + 2πn < x < 2π+ 2πn, nZ . _ _
y = cos x.
cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, nZ; _ +
cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, nZ.
− +
sin x > 0 при 2πn < x < π+ 2πn, nZ;
sin x < 0 при π + 2πn < x < 2π+ 2πn, nZ . _ _
y = cos x.
cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, nZ; _ +
cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, nZ.
− +



![Презентация по теме Тригонометрические функции Функция y = cosxГрафик функции Свойства функции:D(у) = R. E(у) = Функция y = cosxГрафик функции Свойства функции:D(у) = R. E(у) = [- 1 ; 1]Функция](/img/thumbs/c8c7afed6be1f3960752fee671189421-800x.jpg)



![Презентация по теме Тригонометрические функции Монотонность тригонометрических функций. y = cos x . Функция возрастает на Монотонность тригонометрических функций. y = cos x . Функция возрастает на [ π+ 2πn; 2π+ 2πn], nZ,](/img/thumbs/044319bdd4102c2802e4640c757bac0c-800x.jpg)








