- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме РАЗЛИЧНЫЕ ПРИЁМЫ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
Содержание
- 1. Презентация по теме РАЗЛИЧНЫЕ ПРИЁМЫ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
- 2. Для успешного изучения геометрии необходимо знать не
- 3. Задача и пять методов еёрешения В
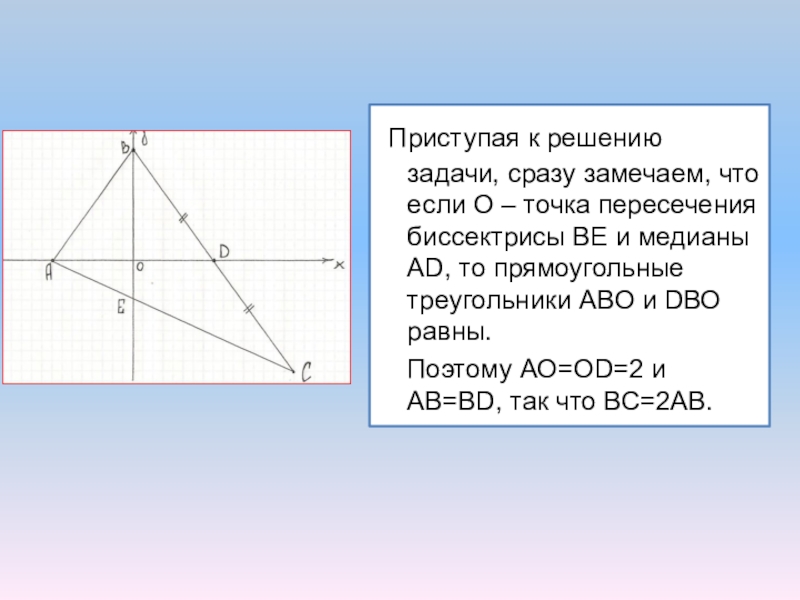
- 4. Приступая к решению задачи, сразу замечаем,
- 5. Способ первый:КООРДИНАТНЫЙПримем точку О за начало прямоугольной
- 6. Способ второй:векторныйВекторы ВЕ и АД выразим через
- 7. Способ третий:аналитическийМедиану AD и биссектрису ВЕ треугольника
- 8. Способ четвертый:тригонометрическийОбозначим АВ=х, угол АВС=2α. По теореме
- 9. Способ пятый:геометрический1.С помощью площадейТак как АО=ОD=2, ВЕ=4
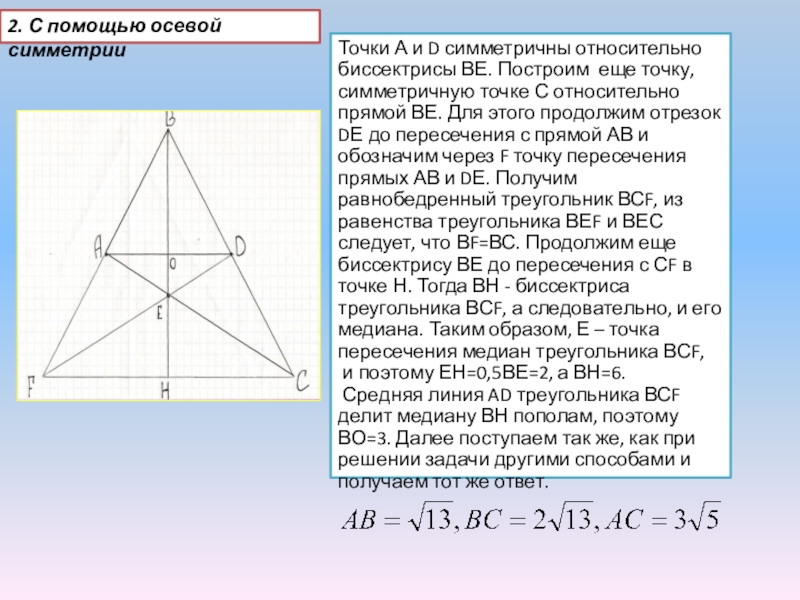
- 10. 2. С помощью осевой симметрии Точки А
- 11. 3. По теореме о средней линии треугольникаПроведем
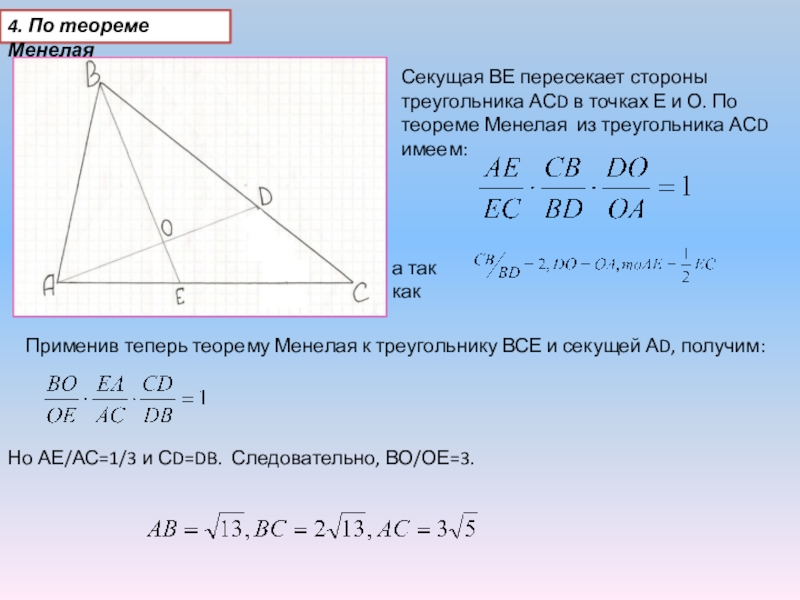
- 12. 4. По теореме МенелаяСекущая ВЕ пересекает стороны
- 13. РЕШЕНИЕ СТЕРЕОМЕТРИЧЕСКОЙ ЗАДАЧИПодготовительный этапАлгоритм построения уравнения плоскости:1.
- 14. Формула нахождения угла между прямыми в пространстве:где
- 15. Формула нахождения угла между прямой и плоскостьюгде
- 16. Рассмотрим применение данной теории на примере решения
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
Слайд 2Для успешного изучения геометрии
необходимо знать
не только основные формулы и
теоремы,
методами решения задач.
Слайд 3Задача
и пять методов её
решения
В треугольнике АВС биссектриса ВЕ
Слайд 4 Приступая к решению задачи, сразу замечаем, что если О –
Поэтому АО=ОD=2 и АВ=BD, так что ВС=2АВ.
Слайд 5Способ первый:
КООРДИНАТНЫЙ
Примем точку О за начало прямоугольной системы координат, оси Ох
В данной системе точки A, D, B имеют координаты:
А (-2;0), D (2;0) и В (0;b).
Для того чтобы определить длины сторон треугольника АВС, надо найти число b. Выразим через b координаты точек С и Е. Так как D – середина отрезка ВС, то С (4;-b). Для точки Е имеем координаты (0;у). Вторую координату точки Е найдем, пользуясь, тем что точка Е принадлежит прямой АС. Уравнение прямой АС имеет вид:
Координаты точки Е (0;у) удовлетворяют этому уравнению. Подставив в него 0 вместо х, получим: . Следовательно, . По условию задачи ВЕ=4, значит, , или b=3.
Итак, А (-2;0), В (0;3), С (4;-3). Зная координаты вершин треугольника АВС, найдем его стороны, используя формулу нахождения расстояния между двумя точками на плоскости
Слайд 6Способ второй:
векторный
Векторы ВЕ и АД выразим через а и с.Так как
Согласно вычитанию векторов, имеем:
Длины векторов ВЕ и АD известны. Пусть
Вычислив скалярные квадраты вектором ВЕ и АD, получим уравнения:
Найдем теперь сторону АС, пользуясь векторной формулировкой теоремы косинусов:
Подставим найденные выше значения и получим:
Слайд 7Способ третий:
аналитический
Медиану AD и биссектрису ВЕ треугольника АВС выразим через длины
Пусть АВ=х, АЕ=у, тогда ВС=2х и СЕ=2у. Получим систему уравнений:
Х
Y
Слайд 8Способ четвертый:
тригонометрический
Обозначим АВ=х, угол АВС=2α. По теореме косинусов из треугольников АВЕ
Учитывая, что СЕ=2АЕ или СЕ2=4АЕ2, получаем: x cos α=3.
Но x cos α=ВО, значит, ВО=3 и ОЕ=1.
Остается, пользуясь теоремой Пифагора, вычислить стороны треугольника АВС.
Х
Слайд 9Способ пятый:
геометрический
1.С помощью площадей
Так как АО=ОD=2, ВЕ=4 и АD перпендикулярна ВЕ,
Значит, площадь треугольника АВС равна 12.
Поскольку АD-медиана треугольника АВС,
то площадь треугольника АВD равна 6.
Остается применить формулу площади треугольника. Получим: АО*ВО=6.
Но АО=2, значит, ВО=3
Стороны треугольника АВС найдем по теореме Пифагора.
Слайд 102. С помощью осевой симметрии
Точки А и D симметричны относительно
и поэтому ЕН=0,5ВЕ=2, а ВН=6.
Средняя линия AD треугольника ВСF делит медиану ВН пополам, поэтому ВО=3. Далее поступаем так же, как при решении задачи другими способами и получаем тот же ответ.
Слайд 113. По теореме о средней линии треугольника
Проведем среднюю линию DК треугольника
ОЕ – средняя линия
треугольника ADK.
Следовательно:
Так как ВЕ=4, то ОЕ=1 и ВО=3
Из приведенного решения видно, что отношение ВО/ОЕ не зависит от отрезков ВЕ и AD. Найти это отношение можно также, используя лишь тот факт, что АD – медиана треугольника АВС и АО=ОВ, причем без всяких вспомогательных построений.
Слайд 124. По теореме Менелая
Секущая ВЕ пересекает стороны треугольника АСD в точках
а так как
Применив теперь теорему Менелая к треугольнику ВСЕ и секущей АD, получим:
Но АЕ/АС=1/3 и СD=DB. Следовательно, ВО/ОЕ=3.
Слайд 13РЕШЕНИЕ СТЕРЕОМЕТРИЧЕСКОЙ ЗАДАЧИ
Подготовительный этап
Алгоритм построения уравнения плоскости:
1. Найдем координаты трех точек,
2. Зададим произвольную точку М (x, y, z), принадлежащую плоскости.
3.На основе свойства компланарности векторов, составим определитель третьего порядка.
и приравниваем его к 0
4. Вычислив определитель, получим уравнение плоскости Ах +Ву + Сz + D = 0.
Слайд 14Формула нахождения угла между прямыми в пространстве:
где {
Формула нахождения угла между двумя плоскостями:
где {A1,B1,C1},{A2,B2,C2} – направляющие плоскостей.
Слайд 15Формула нахождения угла между прямой и плоскостью
где {
Формула нахождения расстояния от точки М(x0,y0,z0) до плоскости
Пусть плоскость задана уравнением Ах+Ву+Сz+D=0, тогда
Слайд 16Рассмотрим применение данной теории на примере решения задачи:
«Ребро куба ABCDA1
Решение:
Введем прямоугольную систему координат так, что т. B – начало координат, BM лежит на Ox, BC лежит на Oy, B C1 лежит на Oz.
Тогда A(1; 0; 0) B(0; 0; 0) C(0; 1; 0)
D(1; 1; 0) A1(1; 0; 1) B1(0; 0; 1) C1(0; 1; 1) D1(1; 1; 1)
N(1; ; 0) L(0; 1; ).
MB = AB – AM = 1 – = M( ; 0; 0)
Тогда { – 0; 0 – 1; 0 – } {1 – 0; – 1; 0 – }.
Т.е. { ; –1; – } {1; – ; – }.
Пусть т.P(x; y; z) (MNL). Тогда {x; y – 1; z – }.