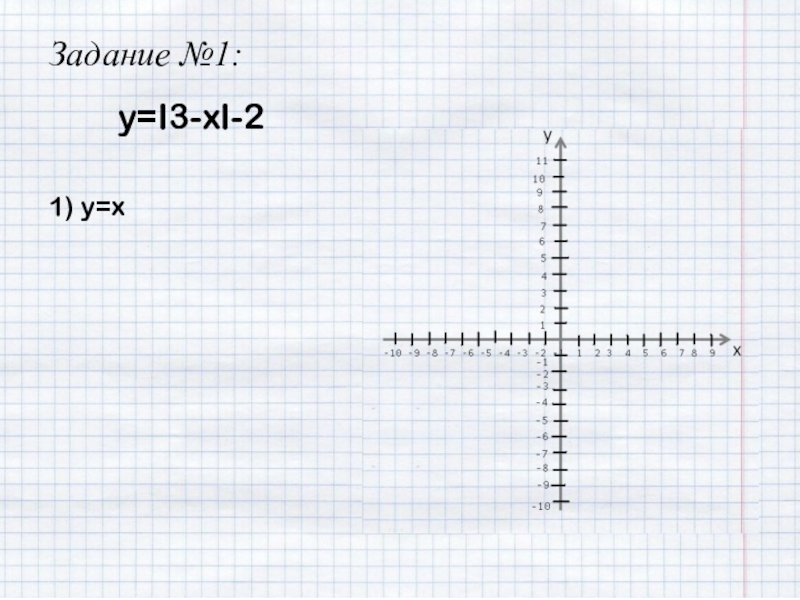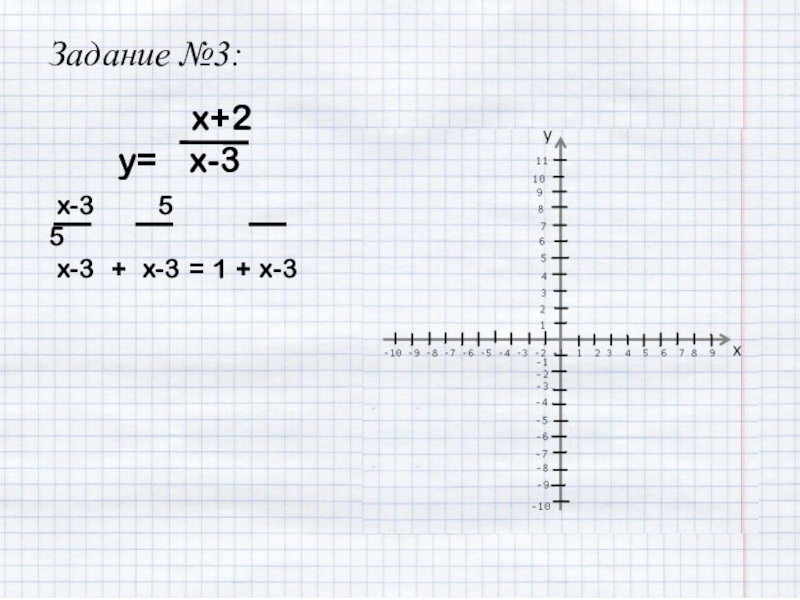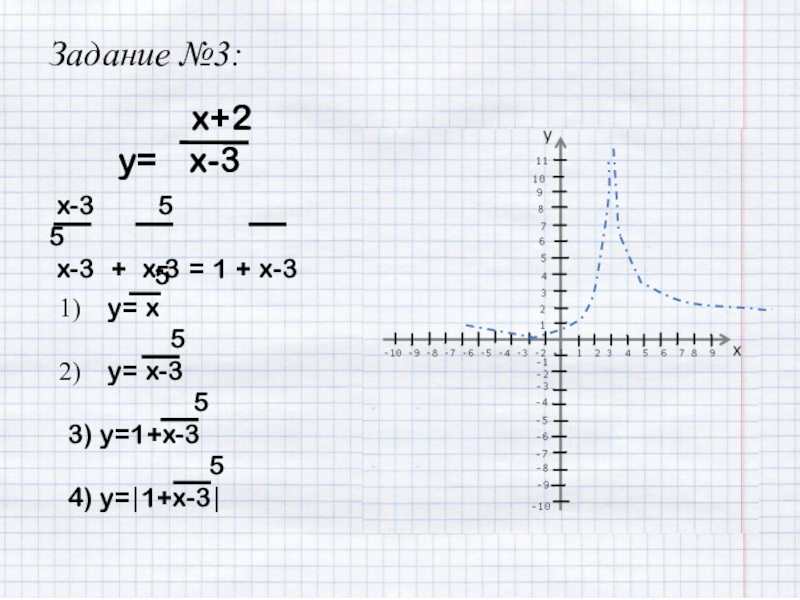А. Л. Кекина
Рогушкина Дарья
Руководитель: Иванченко
Ирина Алексеевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Построение графиков , содержащих модуль
Содержание
- 1. Презентация по теме Построение графиков , содержащих модуль
- 2. Понятие «модуль»Слово «модуль» произошло от латинского слова «modulus»|x|
- 3. Понятие «модуль»Воспользовавшись определением модуля, можно записать:Отсюда можно
- 4. Алгоритм построения графика функции у = f(|x|)Тогда
- 5. Алгоритм построения графика функции у = f(|x|)
- 6. функция у = f|(x)| Для функции у
- 7. Алгоритм построения графика функции у = f|(x)|
- 8. Алгоритм построения графика функции у = f|(x)|
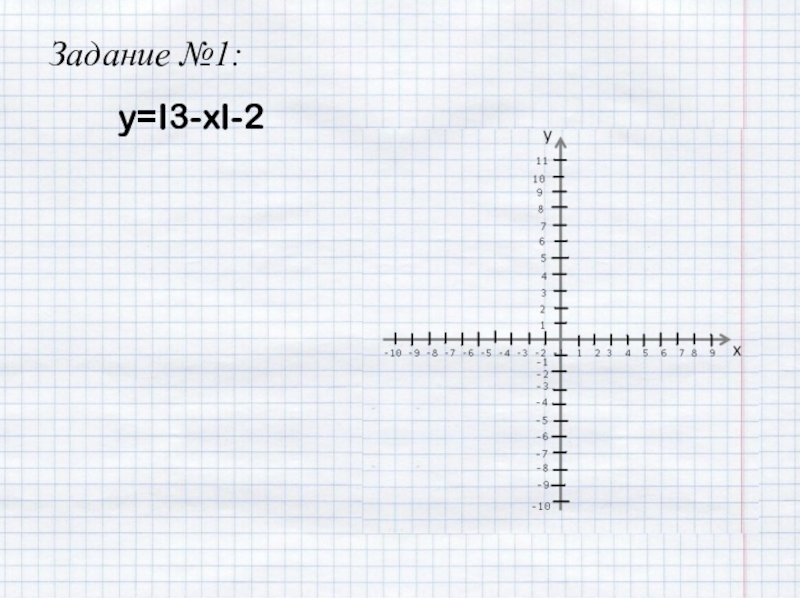
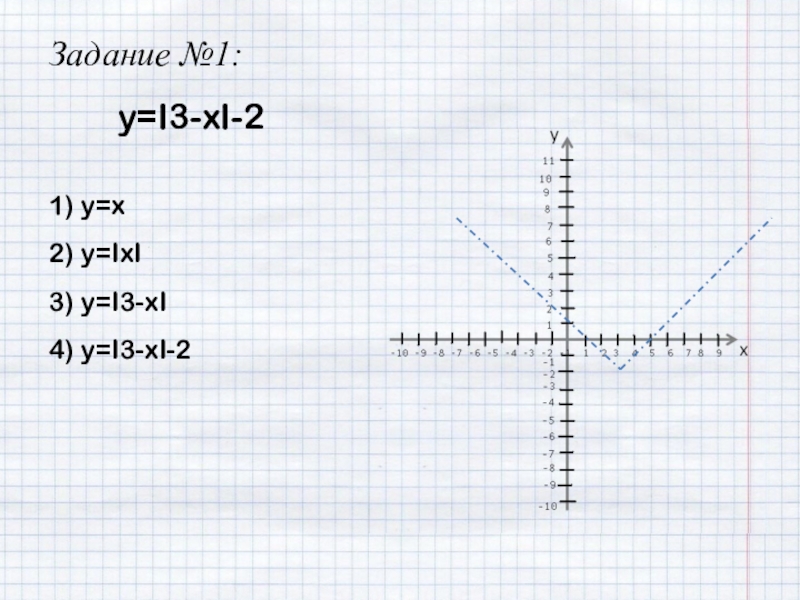
- 9. y=I3-xI-2Задание №1:
- 10. y=I3-xI-2Задание №1:1) y=xху
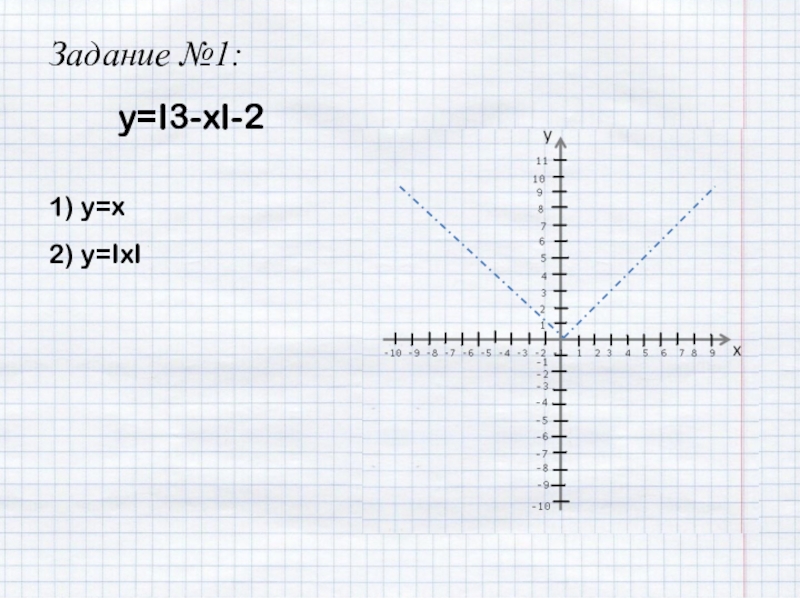
- 11. y=I3-xI-2Задание №1:1) y=x2) y=IxI
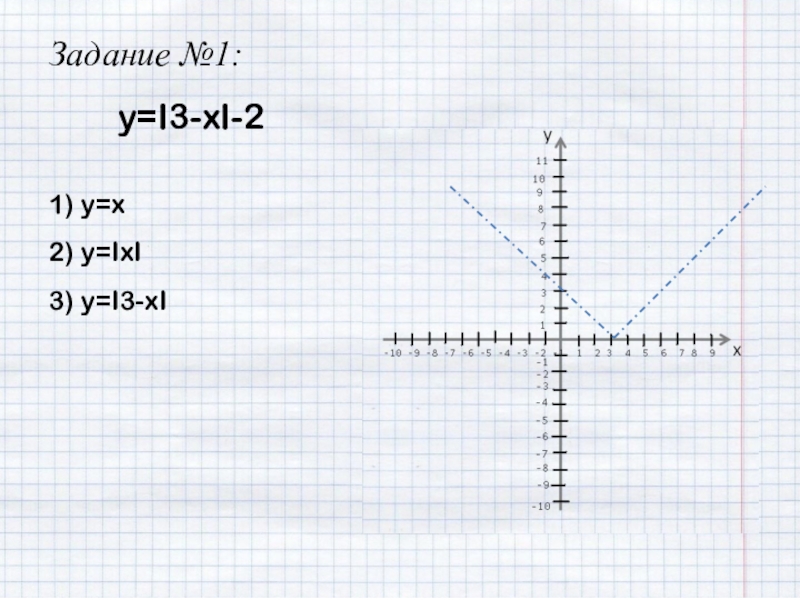
- 12. y=I3-xI-2Задание №1:1) y=x2) y=IxI3) y=I3-xI
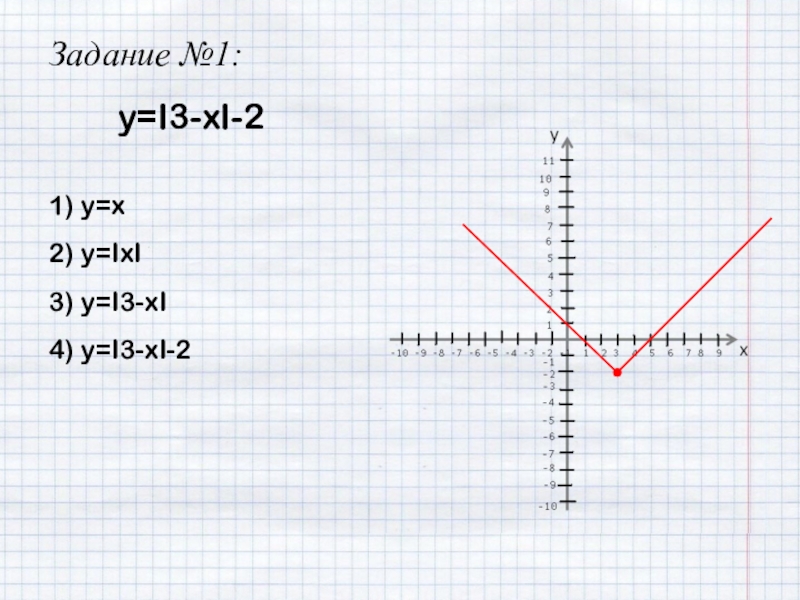
- 13. y=I3-xI-2Задание №1:1) y=x2) y=IxI3) y=I3-xI4) y=I3-xI-2
- 14. y=I3-xI-2Задание №1:1) y=x2) y=IxI3) y=I3-xI4) y=I3-xI-2
- 15. Задание №2:y=I(IxI-2) 2 -3I
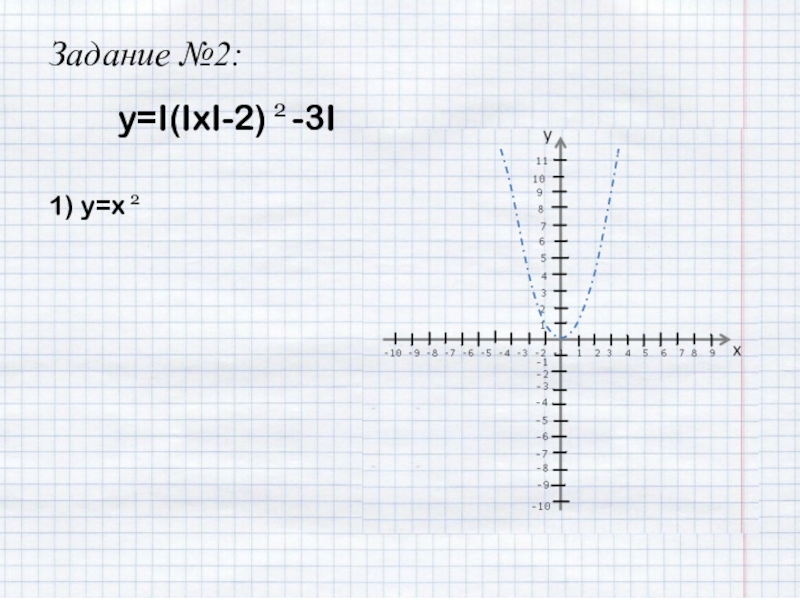
- 16. Задание №2:y=I(IxI-2) 2 -3I1) y=x 2
- 17. Задание №2:y=I(IxI-2) 2 -3I1) y=x 22) y=(x-2) 2
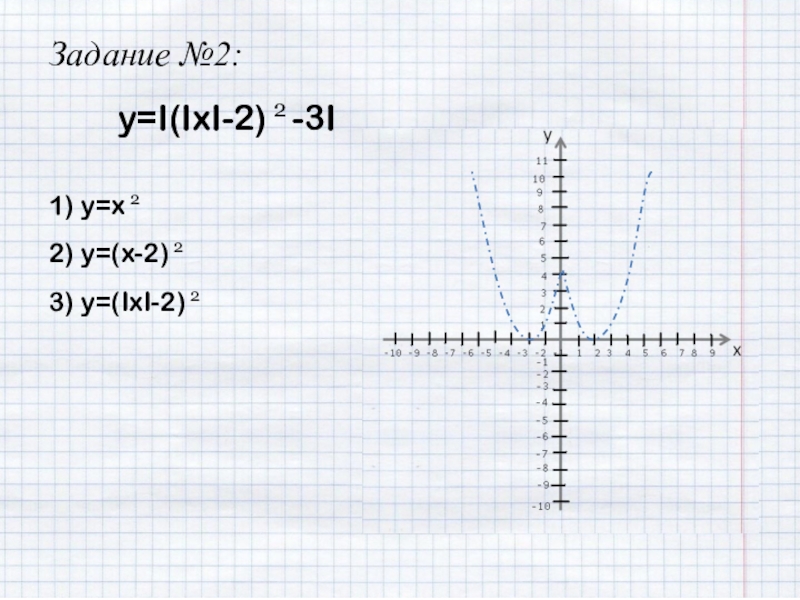
- 18. Задание №2:y=I(IxI-2) 2 -3I1) y=x 22) y=(x-2) 23) y=(IxI-2) 2
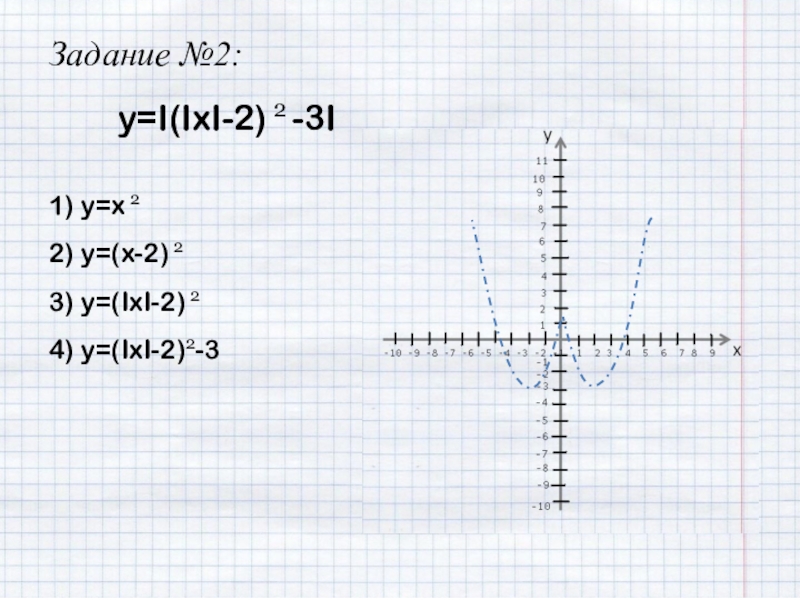
- 19. Задание №2:y=I(IxI-2) 2 -3I1) y=x 22) y=(x-2) 23) y=(IxI-2) 24) y=(IxI-2)2-3
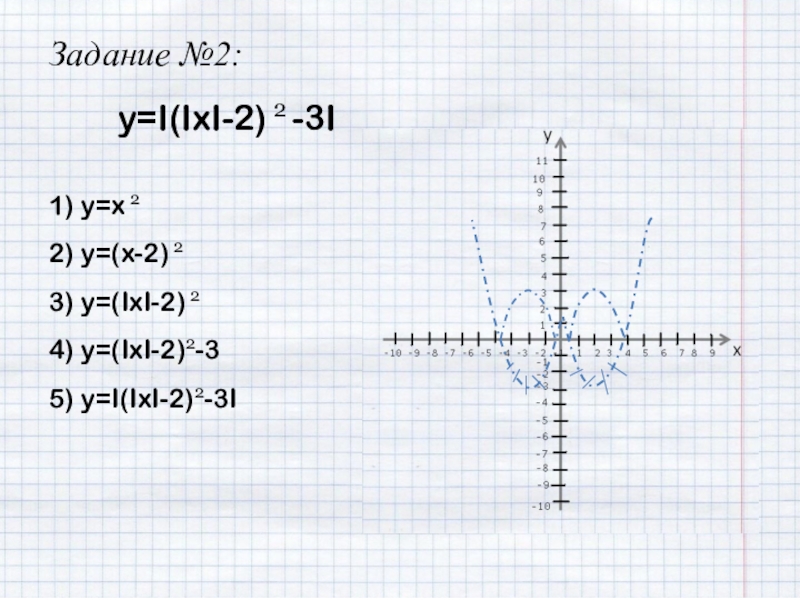
- 20. Задание №2:y=I(IxI-2) 2 -3I1) y=x 22) y=(x-2) 23) y=(IxI-2) 24) y=(IxI-2)2-35) y=I(IxI-2)2-3I
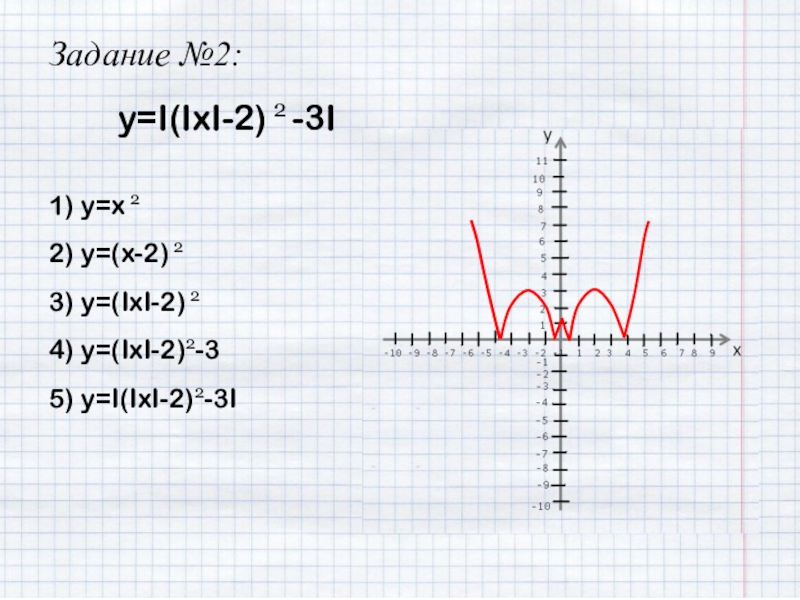
- 21. Задание №2:y=I(IxI-2) 2 -3I1) y=x 22) y=(x-2) 23) y=(IxI-2) 24) y=(IxI-2)2-35) y=I(IxI-2)2-3I
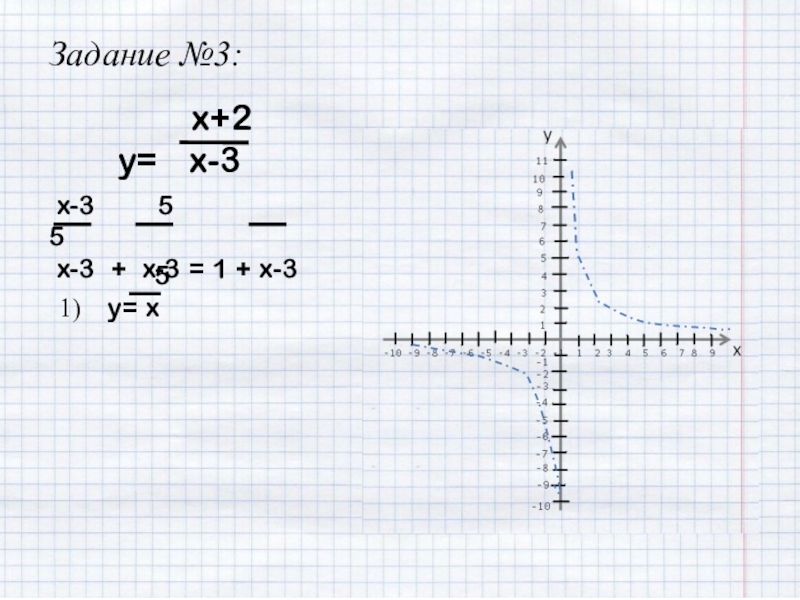
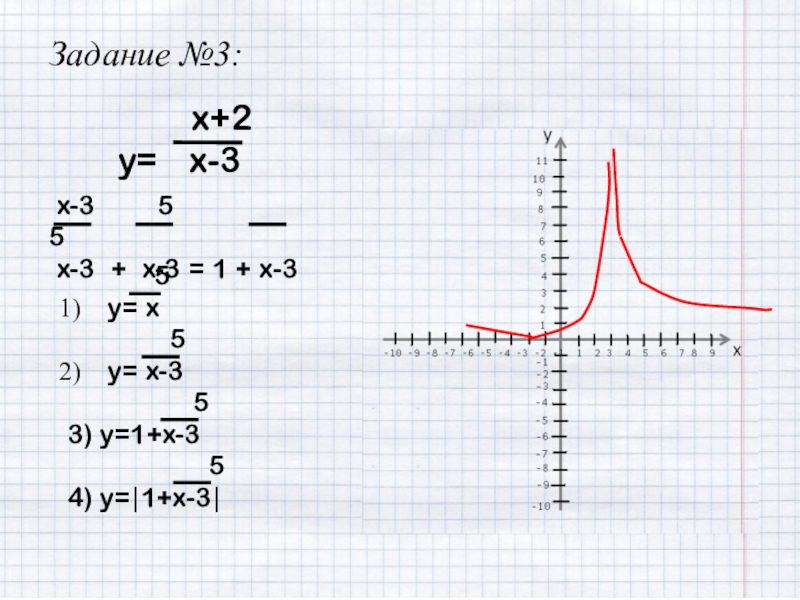
- 22. Задание №3: x+2y=
- 23. Задание №3: x+2y=
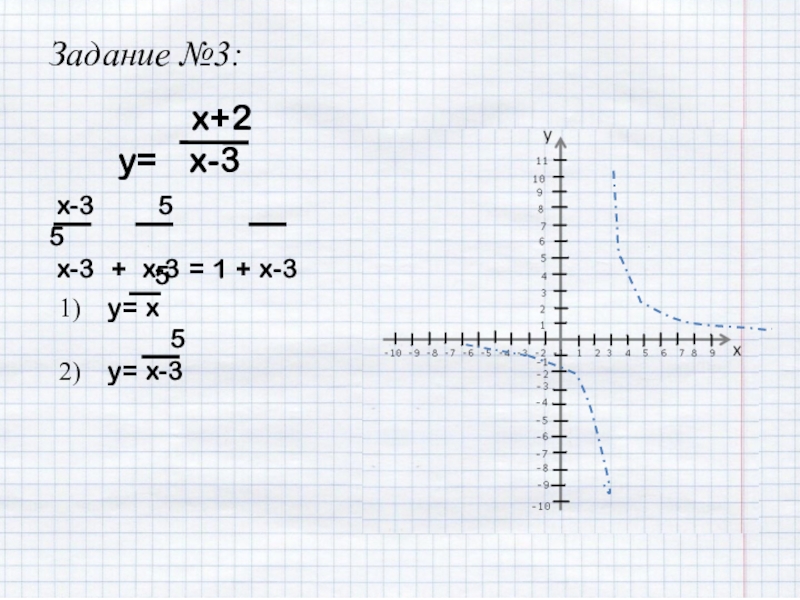
- 24. Задание №3: x+2y=
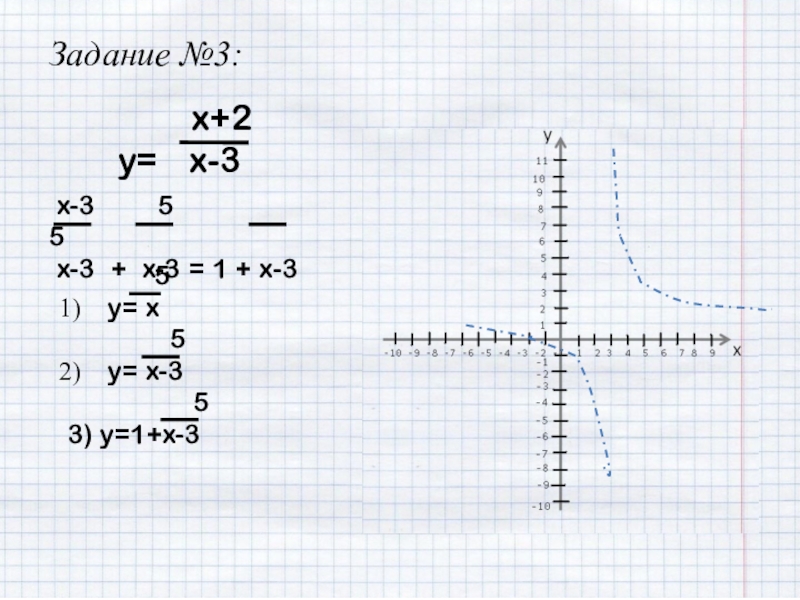
- 25. Задание №3: x+2y=
- 26. Задание №3: x+2y=
- 27. Задание №3: x+2y=
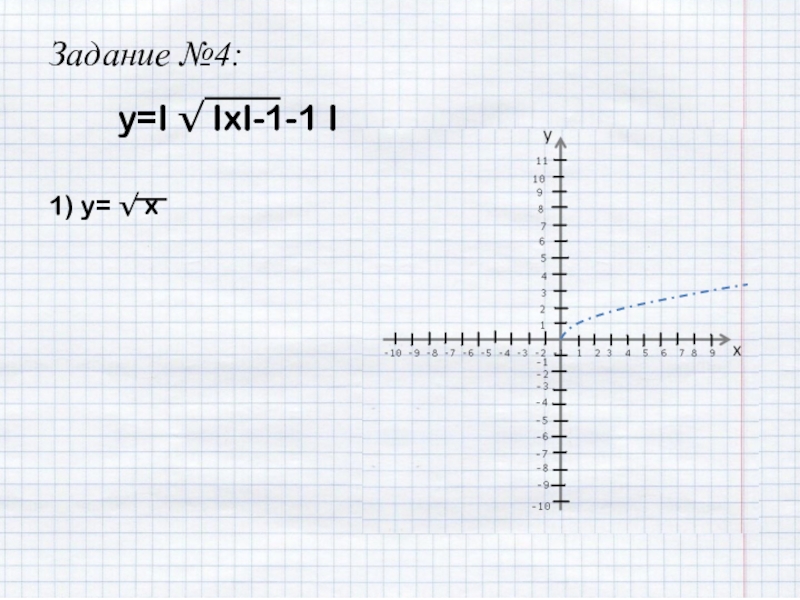
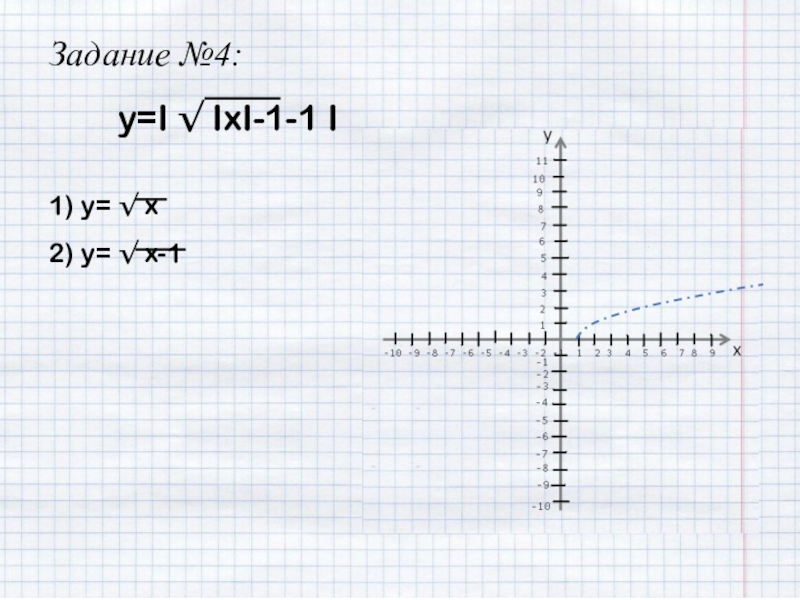
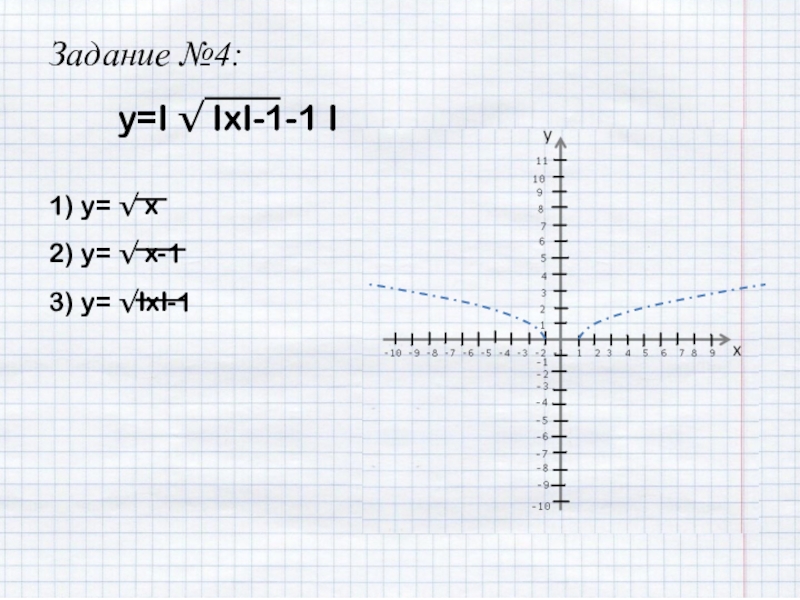
- 28. Задание №4:y=I √ IxI-1-1 I
- 29. Задание №4:y=I √ IxI-1-1 I1) y= √ x
- 30. Задание №4:y=I √ IxI-1-1 I1) y= √ x2) y= √ x-1
- 31. Задание №4:y=I √ IxI-1-1 I1) y= √ x2) y= √ x-13) y= √IxI-1
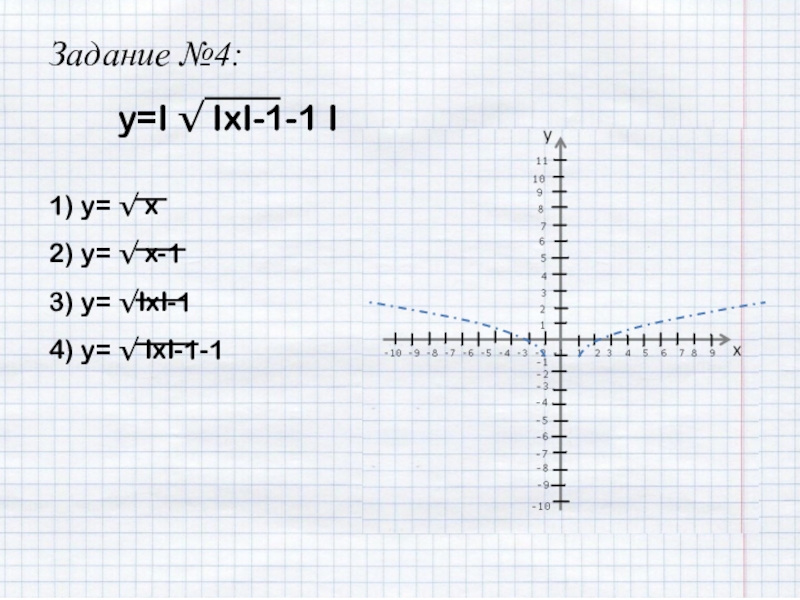
- 32. Задание №4:y=I √ IxI-1-1 I1) y= √ x2) y= √ x-13) y= √IxI-14) y= √ IxI-1-1
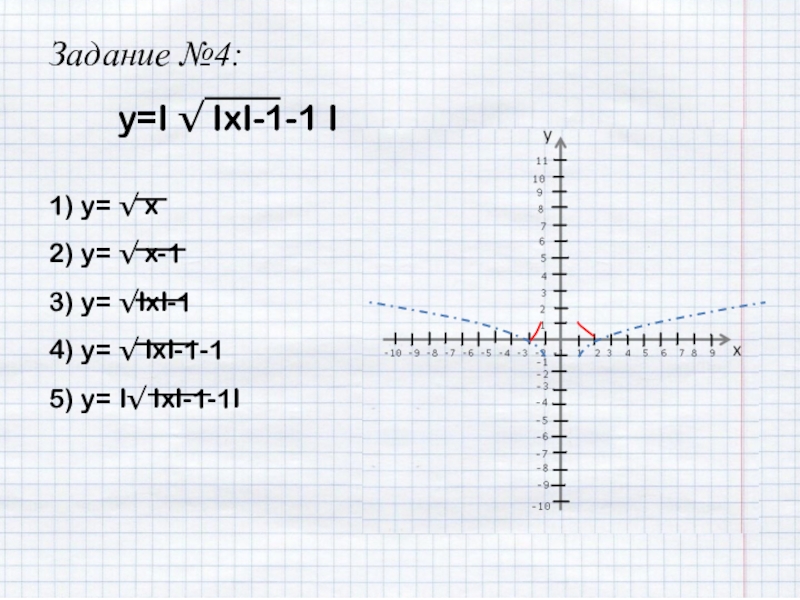
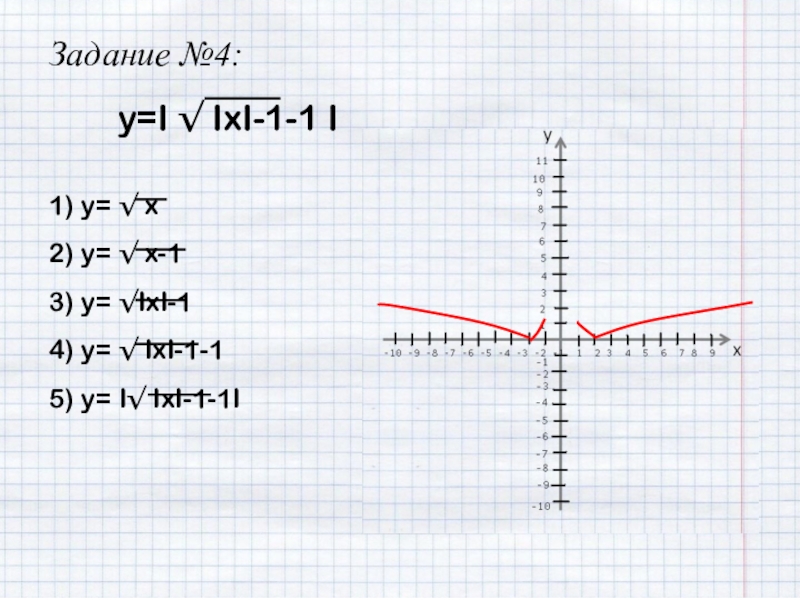
- 33. Задание №4:y=I √ IxI-1-1 I1) y= √
- 34. Задание №4:y=I √ IxI-1-1 I1) y= √
- 35. ВыводТаким образом, мы научились строить графики с
- 36. Спасибо за внимание!
- 37. Источники:http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/524487/Учебник «Алгебра.9 класс». (авт. А.Г. Мерзляк, В.М. Поляков), 2015
Понятие «модуль»Слово «модуль» произошло от латинского слова «modulus»|x|
Слайд 3Понятие «модуль»
Воспользовавшись определением модуля, можно записать:
Отсюда можно сделать вывод, что график
функции у = f(|x|) при х≥0 совпадает с графиком функции у = f(x), а при х < 0 — с графиком функции у = f(- x).
Слайд 4Алгоритм построения графика функции у = f(|x|)
Тогда построение графика функции у
= f(|x|) можно проводить по следующей схеме.
1) Построить ту часть графика функции у = f(x), все точки которой имеют неотрицательные абсциссы;
2) построить ту часть графика функции у = f(- x), все точки которой имеют отрицательные абсциссы.
Объединение этих двух построенных фигур является графиком функции у = f(|x|)
1) Построить ту часть графика функции у = f(x), все точки которой имеют неотрицательные абсциссы;
2) построить ту часть графика функции у = f(- x), все точки которой имеют отрицательные абсциссы.
Объединение этих двух построенных фигур является графиком функции у = f(|x|)
Слайд 5Алгоритм построения графика функции у = f(|x|)
Заметим, что функция у
= f(|x|) является чётной. Поэтому ось ординат является осью симметрии её графика. Тогда график функции у = f(|x|) можно получить по следующей схеме.
1) Построить ту часть графика функции у = f(x), все точки которой имеют неотрицательные абсциссы;
2) построить фигуру, симметричную полученной относительно оси ординат.
Объединение двух построенных фигур является графиком функции у = f(|x|)
1) Построить ту часть графика функции у = f(x), все точки которой имеют неотрицательные абсциссы;
2) построить фигуру, симметричную полученной относительно оси ординат.
Объединение двух построенных фигур является графиком функции у = f(|x|)
Слайд 6функция у = f|(x)|
Для функции у = f|(x)| можно записать:
Отсюда
можно сделать такой вывод: график функции у = |f(х)| при всех х, для которых f(x) ≥ 0, совпадает с графиком функции у = f(x), а при всех х, для которых f(x) < 0, — с графиком функции у = - f(х).
Слайд 7Алгоритм построения графика функции у = f|(x)|
Тогда построение графика функции
у = |f(х)| можно проводить по следующей схеме.
1) Построить ту часть графика функции у = f(x), все точки которой
имеют неотрицательные ординаты;
2) построить ту часть графика функции у = - f(x), все точки которой имеют положительные ординаты.
Объединение двух построенных фигур является графиком функции у = |f(х)|
1) Построить ту часть графика функции у = f(x), все точки которой
имеют неотрицательные ординаты;
2) построить ту часть графика функции у = - f(x), все точки которой имеют положительные ординаты.
Объединение двух построенных фигур является графиком функции у = |f(х)|
Слайд 8Алгоритм построения графика функции у = f|(x)|
Поскольку графики функций у
= f(x) и у = - f(x) симметричны относительно оси абсцисс, то искомый график можно получить по следующей схеме.
1) Ту часть графика функции у = f(x), точки которой имеют неотрицательные ординаты, оставить без изменений;
2) построить фигуру, симметричную относительно оси абсцисс той части графика функции у = f(x), точки которой имеют отрицательные ординаты.
Объединение этих двух построенных фигур и составит график функции у = |f(х)|
1) Ту часть графика функции у = f(x), точки которой имеют неотрицательные ординаты, оставить без изменений;
2) построить фигуру, симметричную относительно оси абсцисс той части графика функции у = f(x), точки которой имеют отрицательные ординаты.
Объединение этих двух построенных фигур и составит график функции у = |f(х)|
Слайд 20Задание №2:
y=I(IxI-2) 2 -3I
1) y=x 2
2) y=(x-2) 2
3) y=(IxI-2) 2
4) y=(IxI-2)2-3
5)
y=I(IxI-2)2-3I
Слайд 21Задание №2:
y=I(IxI-2) 2 -3I
1) y=x 2
2) y=(x-2) 2
3) y=(IxI-2) 2
4) y=(IxI-2)2-3
5)
y=I(IxI-2)2-3I
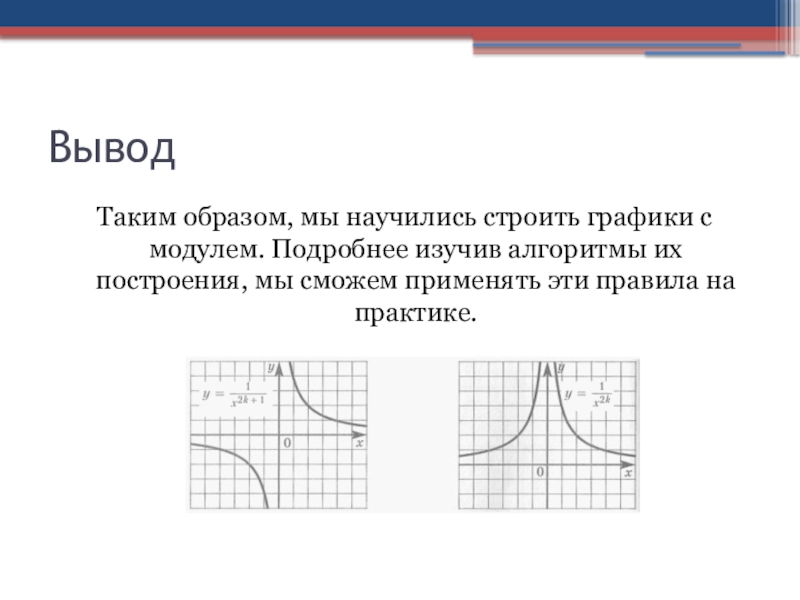
Слайд 35Вывод
Таким образом, мы научились строить графики с модулем. Подробнее изучив алгоритмы
их построения, мы сможем применять эти правила на практике.