Презентация, доклад по теме Определённый интеграл и его свойства

Содержание

1. Презентация по теме Определённый интеграл и его свойства
2. Криволинейная трапецияФигура, ограниченная линиями y=f(x), х=a, x=b,
3. Криволинейная трапеция
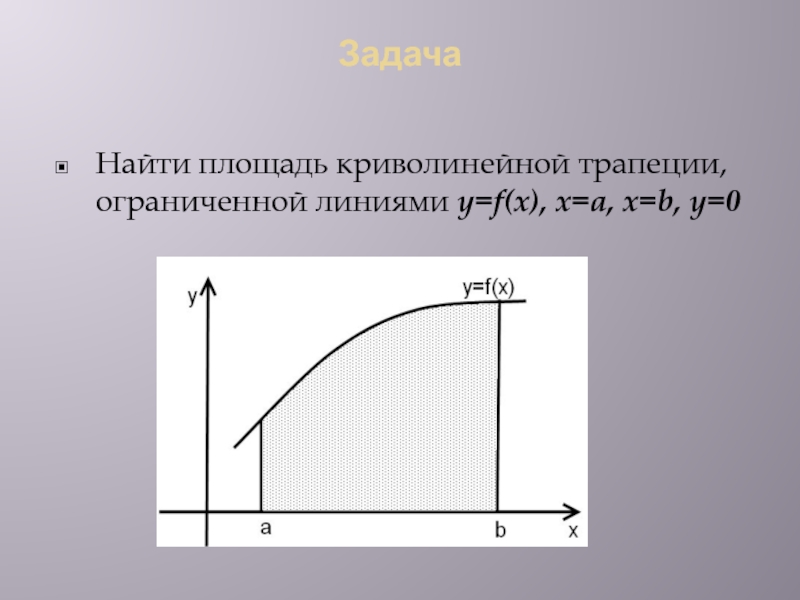
4. ЗадачаНайти площадь криволинейной трапеции, ограниченной линиями y=f(x), х=a, x=b, y=0
5. Проведем вертикальные линии
6. Площадь криволинейной трапеции определённый интегралa, b – пределы интегрирования - подъинтегральная функция
7. Свойства определённого интеграла
8. Свойства определённого интеграла
9. Свойства определённого интеграла
10. Свойства определённого интегралаПусть точка
11. Формула Ньютона-ЛейбницаПусть функция y=f(x) непрерывна на отрезке

Криволинейная трапецияФигура, ограниченная линиями y=f(x), х=a, x=b, y=0 называется криволинейной трапецией.Причем функция y =f(x) должна существовать на отрезке , быть непрерывной и неотрицательной на этом отрезке

Главная
Алгебра
Презентация по теме Определённый интеграл и его свойства

Слайд 1Понятие определённого интеграла

Слайд 2Криволинейная трапеция
Фигура, ограниченная линиями y=f(x), х=a, x=b, y=0 называется криволинейной трапецией.
Причем

функция y =f(x) должна существовать на отрезке , быть
непрерывной и
неотрицательной
на этом отрезке

Криволинейная трапецияФигура, ограниченная линиями y=f(x), х=a, x=b, y=0 называется криволинейной трапецией.Причем функция y =f(x) должна существовать на

Слайд 3Криволинейная трапеция

Слайд 4Задача
Найти площадь криволинейной трапеции, ограниченной линиями y=f(x), х=a, x=b, y=0

Слайд 5Проведем вертикальные
линии x=xi,

криволинейная
трапеция
разобьется на n частей
Площадь прямоугольника равна

f(ci)

-интегральная сумма

Проведем вертикальные линии x=xi, криволинейная

Слайд 6Площадь криволинейной трапеции

определённый интеграл
a, b – пределы интегрирования
-

подъинтегральная функция

Слайд 7Свойства определённого интеграла

Слайд 8Свойства определённого интеграла

Слайд 9Свойства определённого интеграла

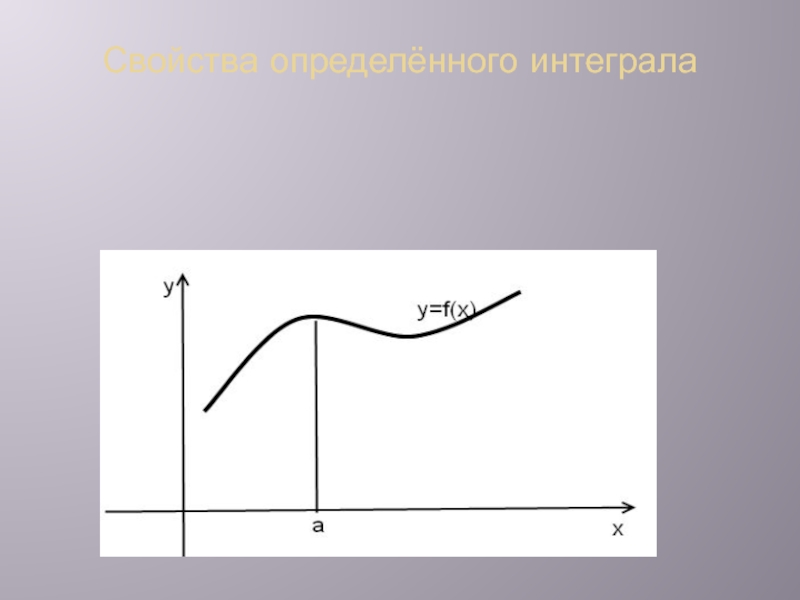
Слайд 10Свойства определённого интеграла
Пусть точка

, тогда определённый интеграл от функции на отрезке равен сумме интегралов на частичных промежутках и

Свойства определённого интегралаПусть точка , тогда определённый интеграл

Слайд 11 Формула Ньютона-Лейбница

Пусть функция y=f(x) непрерывна на отрезке [a,b] и F(x) -

какая-либо первообразная для f(x) на [a,b] . Тогда определенный интеграл от функции f(x) на [a,b] равен приросту первообразной F(x) на этом отрезке

Формула Ньютона-ЛейбницаПусть функция y=f(x) непрерывна на отрезке [a,b] и F(x) - какая-либо первообразная для f(x) на [a,b]

Скачать презентацию

Презентация, доклад по теме Определённый интеграл и его свойства

Содержание

Слайд 1Понятие определённого интеграла

Слайд 2Криволинейная трапеция
Фигура, ограниченная линиями y=f(x), х=a, x=b, y=0 называется криволинейной трапецией.
Причем

Слайд 3Криволинейная трапеция

Слайд 4Задача
Найти площадь криволинейной трапеции, ограниченной линиями y=f(x), х=a, x=b, y=0

Слайд 5Проведем вертикальные
линии x=xi,

Слайд 6Площадь криволинейной трапеции

определённый интеграл
a, b – пределы интегрирования
-

Слайд 7Свойства определённого интеграла

Слайд 8Свойства определённого интеграла

Слайд 9Свойства определённого интеграла

Слайд 10Свойства определённого интеграла
Пусть точка

Слайд 11 Формула Ньютона-Лейбница

Пусть функция y=f(x) непрерывна на отрезке [a,b] и F(x) -

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по теме Определённый интеграл и его свойства

Содержание

Слайд 1Понятие определённого интеграла

Слайд 2Криволинейная трапецияФигура, ограниченная линиями y=f(x), х=a, x=b, y=0 называется криволинейной трапецией.Причем

Слайд 3Криволинейная трапеция

Слайд 4ЗадачаНайти площадь криволинейной трапеции, ограниченной линиями y=f(x), х=a, x=b, y=0

Слайд 5Проведем вертикальные линии x=xi,

Слайд 6Площадь криволинейной трапеции определённый интегралa, b – пределы интегрирования -

Слайд 7Свойства определённого интеграла

Слайд 8Свойства определённого интеграла

Слайд 9Свойства определённого интеграла

Слайд 10Свойства определённого интегралаПусть точка

Слайд 11 Формула Ньютона-ЛейбницаПусть функция y=f(x) непрерывна на отрезке [a,b] и F(x) -

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 2Криволинейная трапеция
Фигура, ограниченная линиями y=f(x), х=a, x=b, y=0 называется криволинейной трапецией.
Причем

Слайд 4Задача
Найти площадь криволинейной трапеции, ограниченной линиями y=f(x), х=a, x=b, y=0

Слайд 5Проведем вертикальные
линии x=xi,

Слайд 6Площадь криволинейной трапеции

определённый интеграл
a, b – пределы интегрирования
-

Слайд 10Свойства определённого интеграла
Пусть точка

Слайд 11 Формула Ньютона-Лейбница

Пусть функция y=f(x) непрерывна на отрезке [a,b] и F(x) -