- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Обобщающий урок по теме ГРАФИКИ
Содержание
- 1. Презентация по теме Обобщающий урок по теме ГРАФИКИ
- 2. ЦЕЛЬ УРОКА: Повторить
- 3. Слайд 3
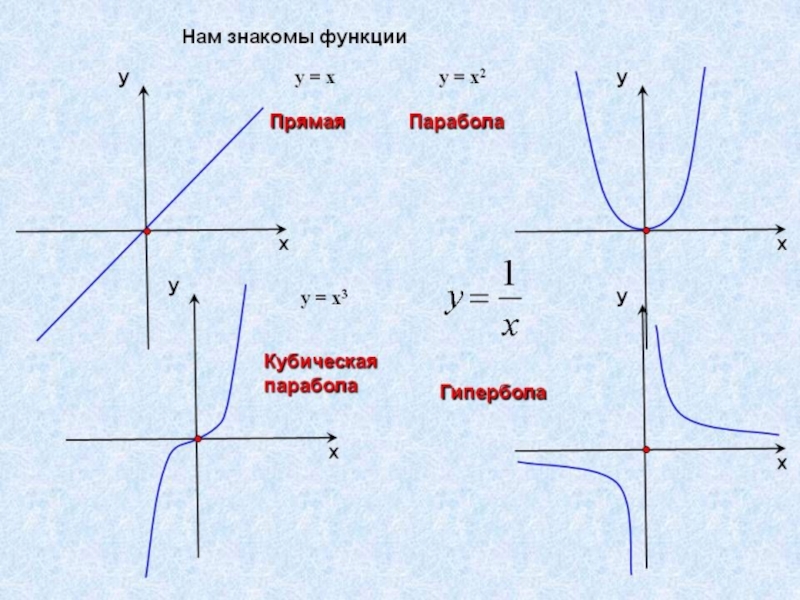
- 4. Из данных функций выберите те, которые являются
- 5. XY01Построим график функции у = 2х +
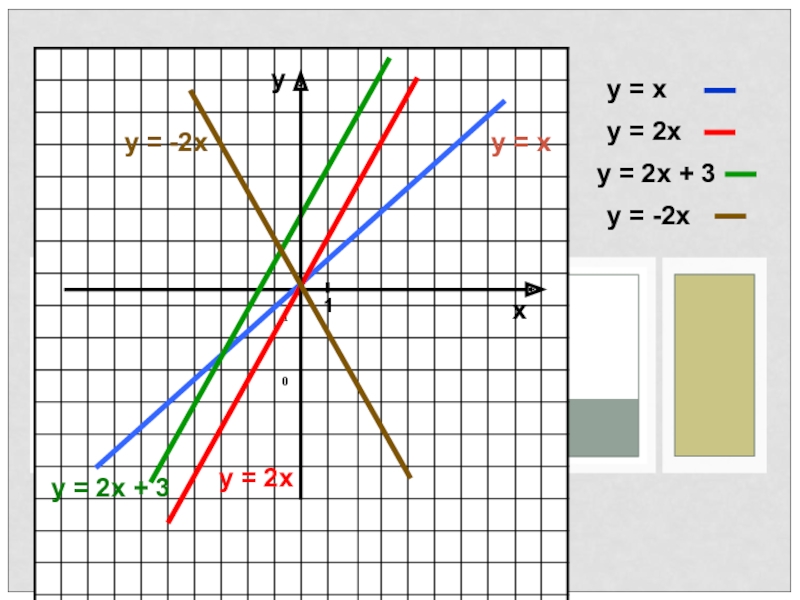
- 6. ху = ху = 2ху = 2х
- 7. Слайд 7
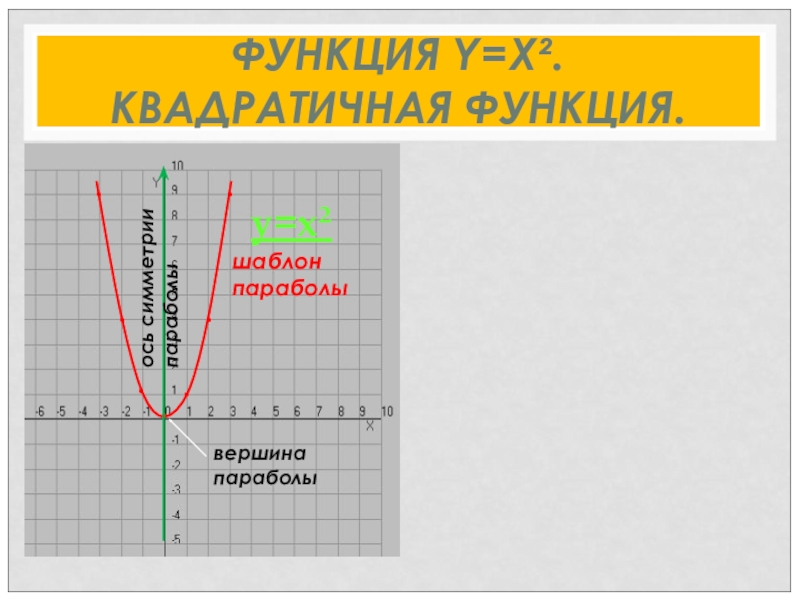
- 8. ФУНКЦИЯ Y=X². КВАДРАТИЧНАЯ ФУНКЦИЯ. • • • • •••y=x²шаблон параболывершина параболыось симметрии параболы
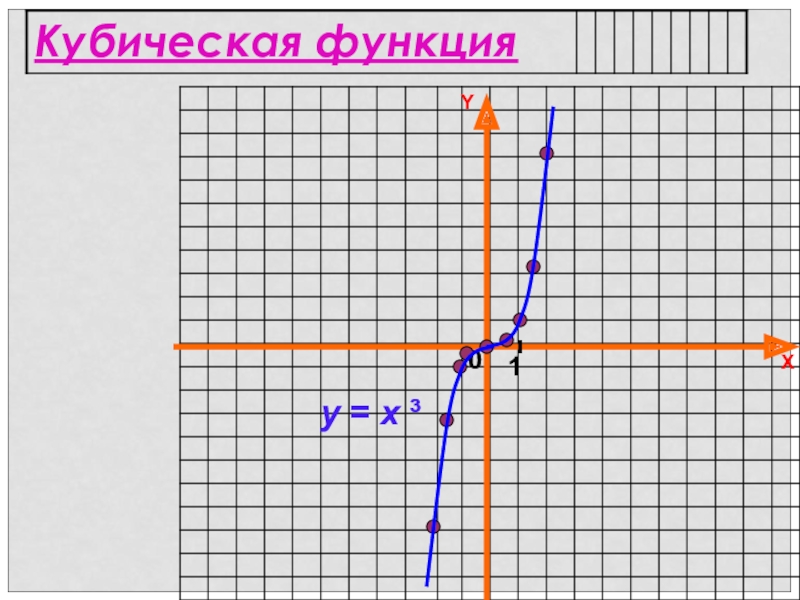
- 9. XY01y = x ³
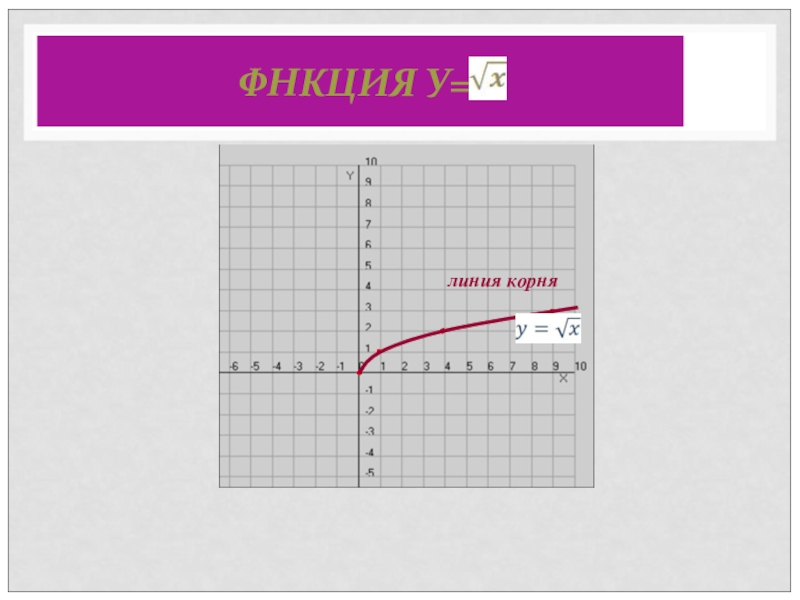
- 10. ФНКЦИЯ У=. •линия корня
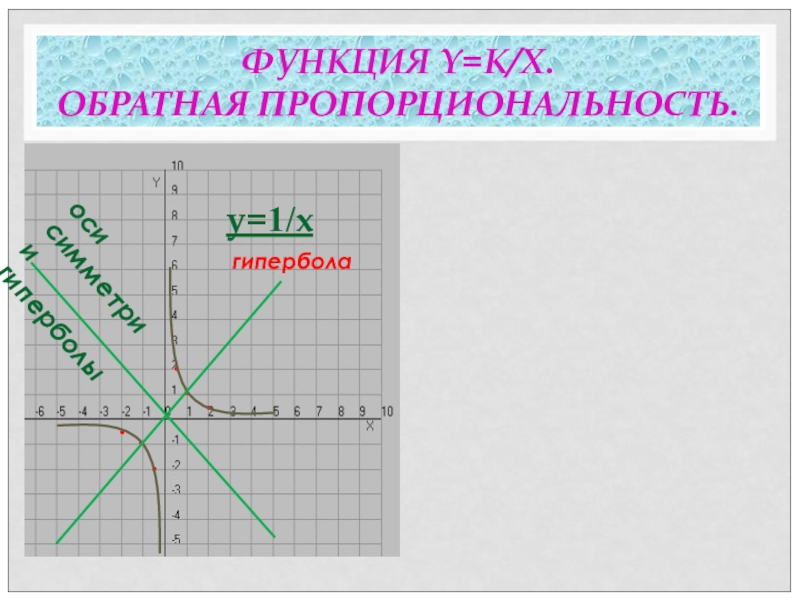
- 11. ФУНКЦИЯ Y=K/X. ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ. • • • •• •y=1/xгиперболаоси симметрии гиперболы
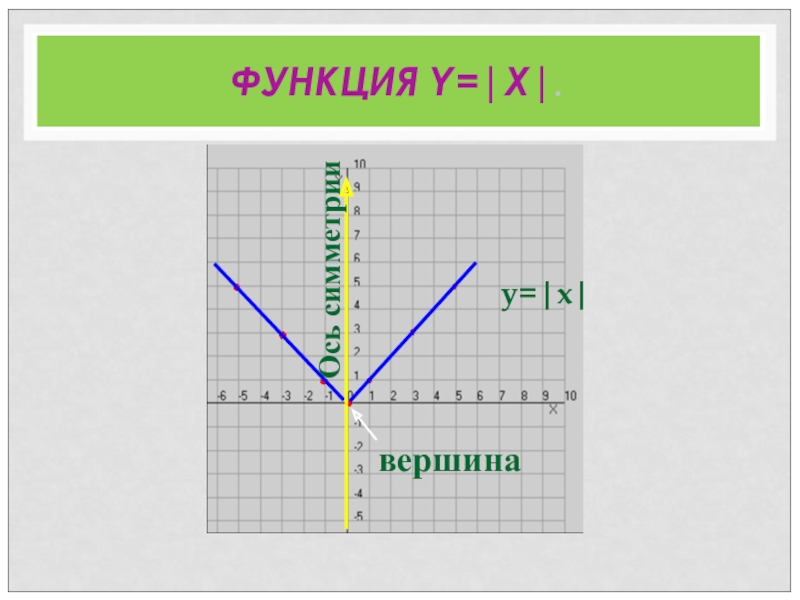
- 12. ФУНКЦИЯ Y=|X|.y=|x|вершинаОсь симметрии
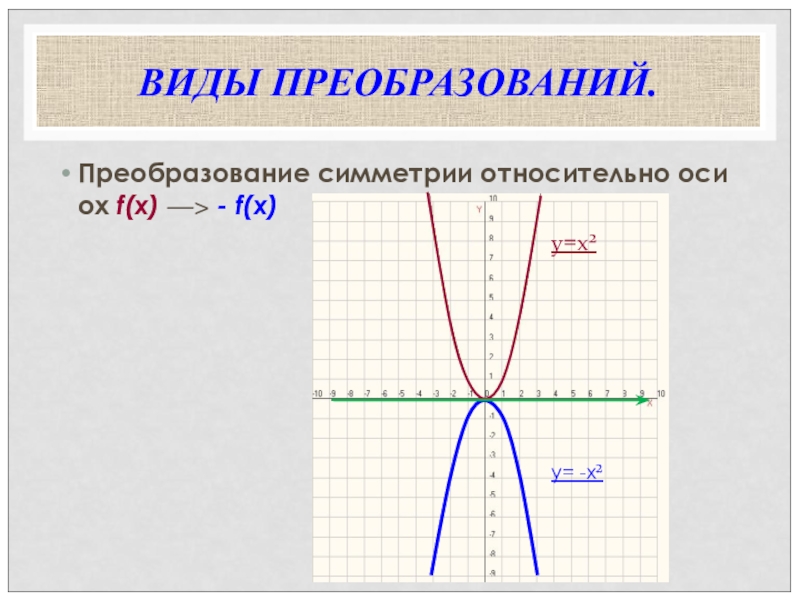
- 13. ВИДЫ ПРЕОБРАЗОВАНИЙ.Преобразование симметрии относительно оси оx f(x) ―> - f(x)y=x²y= -x²
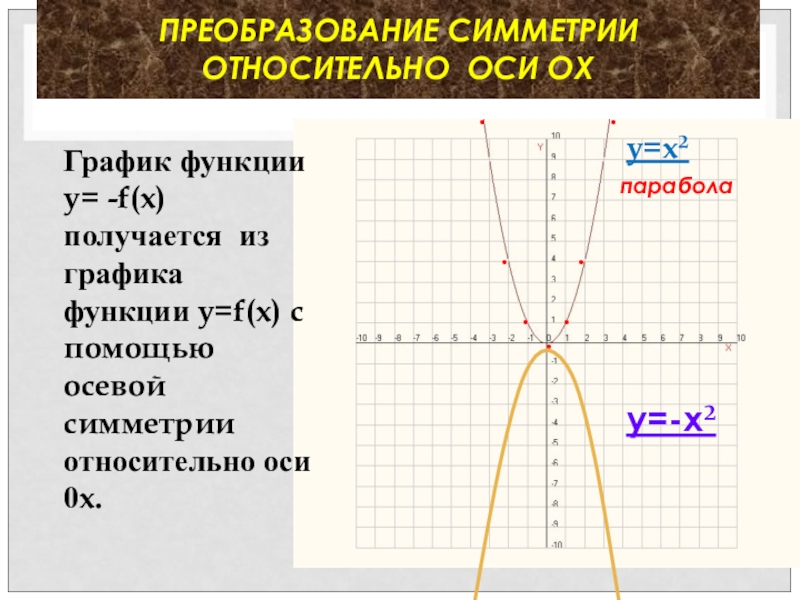
- 14. ПРЕОБРАЗОВАНИЕ СИММЕТРИИ ОТНОСИТЕЛЬНО ОСИ ОХ •
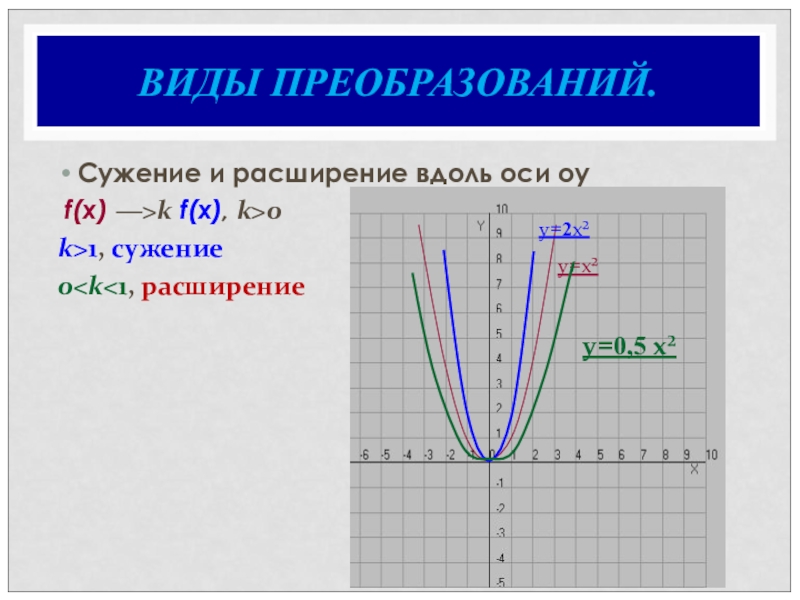
- 15. ВИДЫ ПРЕОБРАЗОВАНИЙ.Сужение и расширение вдоль оси оy f(x) ―>k f(x), k>0k>1, сужение0
- 16. k>1График функции y=2x² получается сжатиемграфика функции y=x²
- 17. Слайд 17
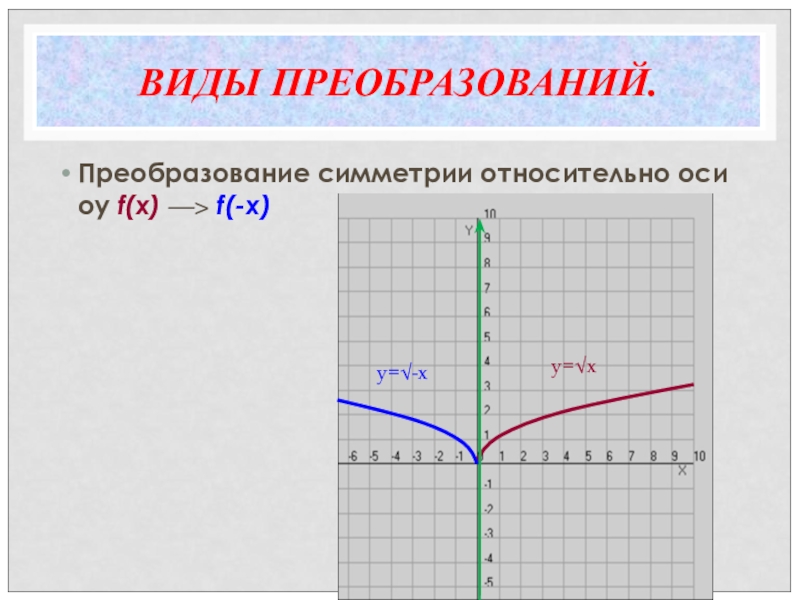
- 18. ВИДЫ ПРЕОБРАЗОВАНИЙ.Преобразование симметрии относительно оси оy f(x) ―> f(-x)y=√xy=√-x
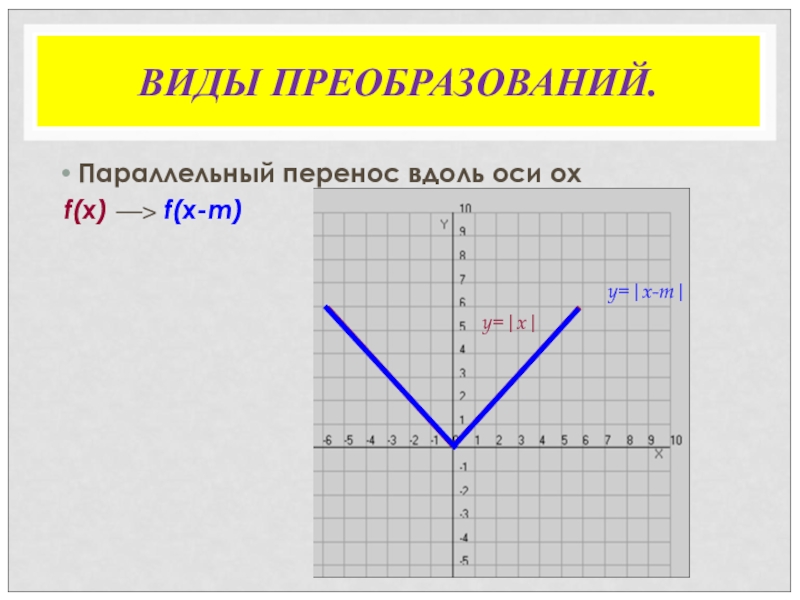
- 19. ВИДЫ ПРЕОБРАЗОВАНИЙ.Параллельный перенос вдоль оси оx f(x) ―> f(x-m)y=|x|y=|x-m|
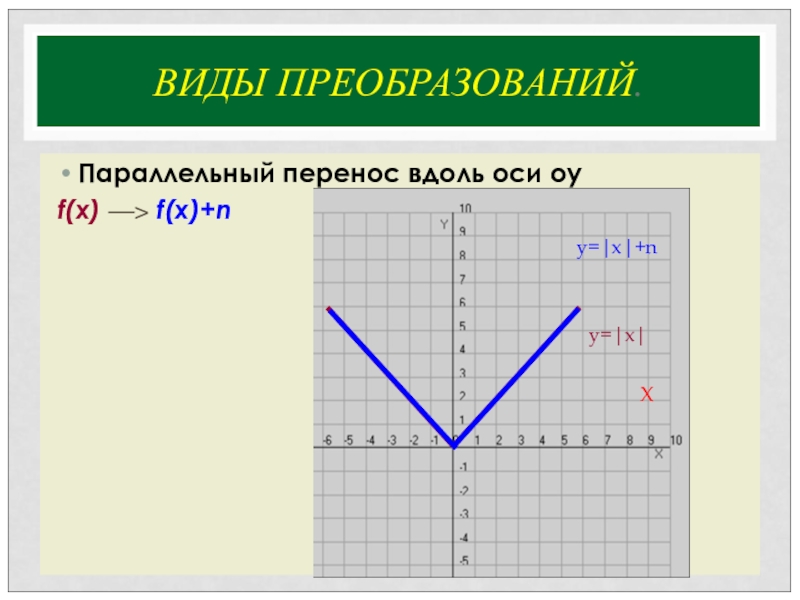
- 20. ВИДЫ ПРЕОБРАЗОВАНИЙ.Параллельный перенос вдоль оси оyf(x) ―> f(x)+n y=|x|Xy=|x|+n
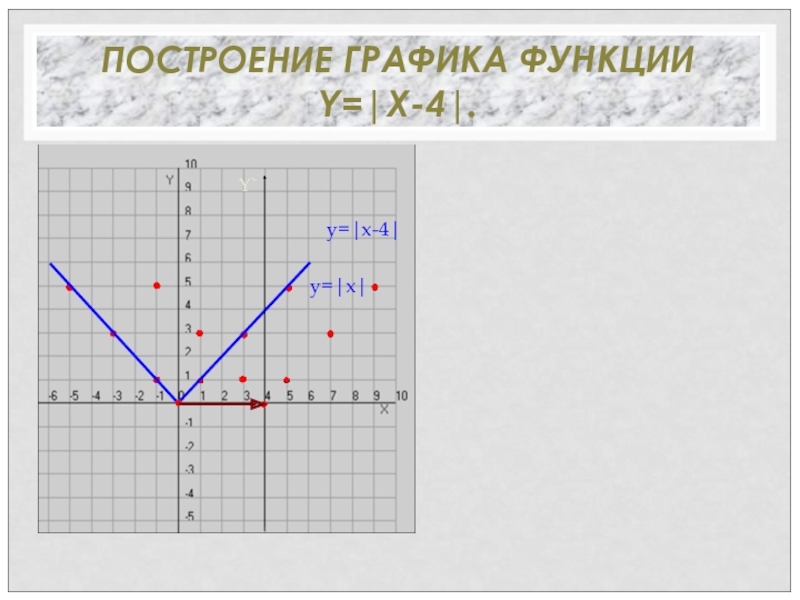
- 21. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y=|X-4|.y=|x|Y`y=|x-4|
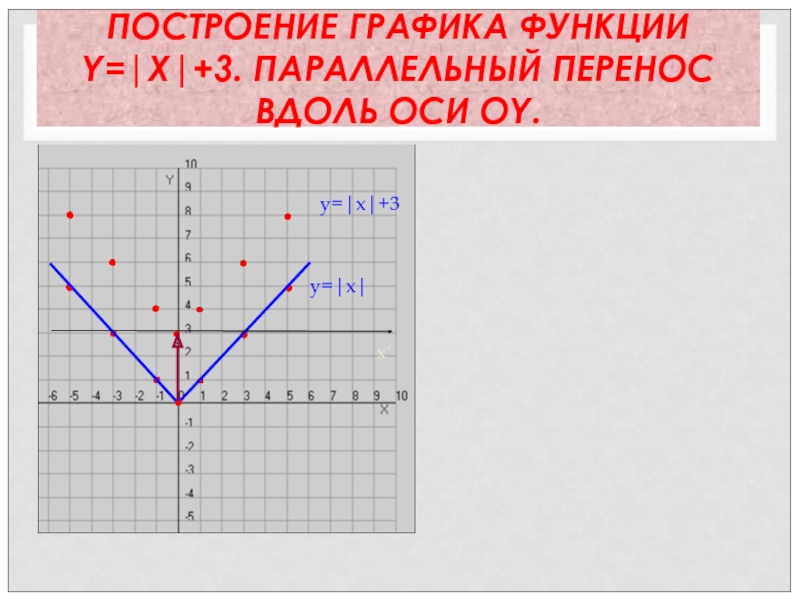
- 22. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y=|X|+3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ ОY.y=|x|x´y=|x|+3
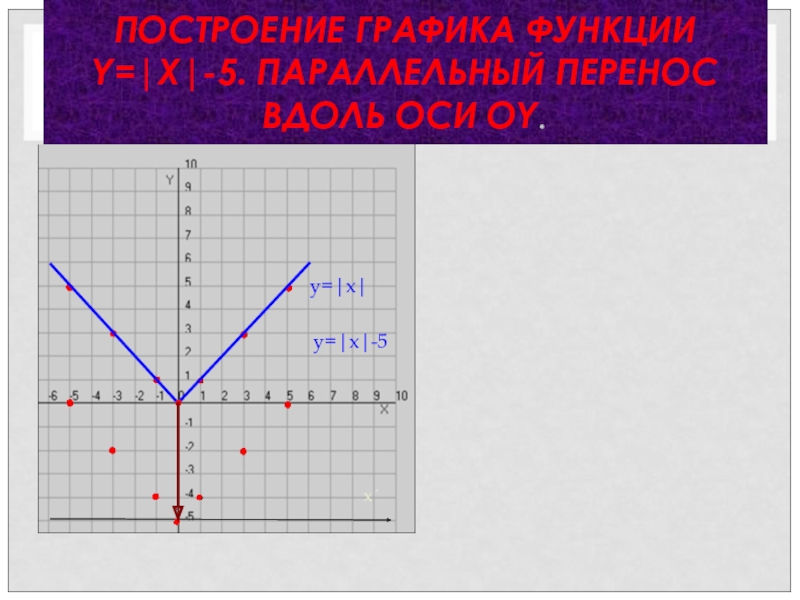
- 23. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y=|X|-5. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ ОY.y=|x|x´y=|x|-5
- 24. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y=3|X|. СУЖЕНИЕ К ОСИ ОY .y=|x|y=3|x|
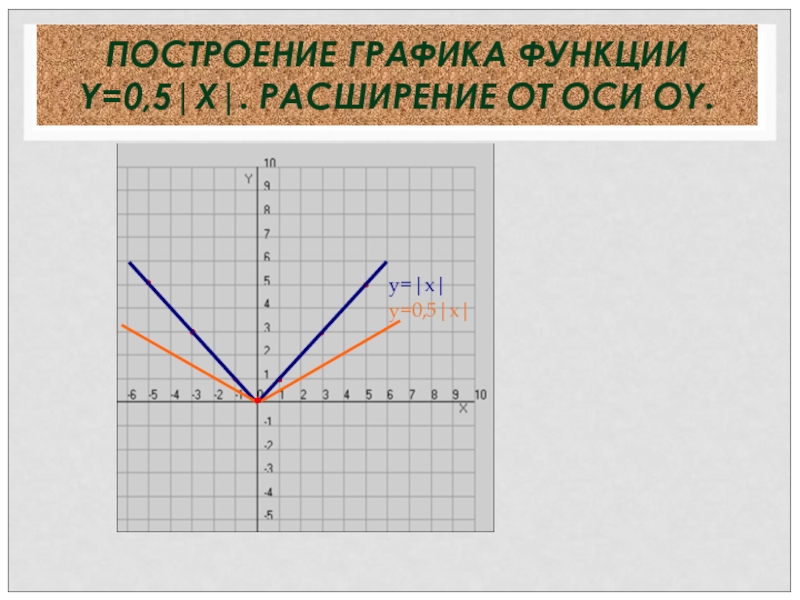
- 25. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y=0,5|Х|. РАСШИРЕНИЕ ОТ ОСИ ОY.y=|x|y=0,5|x|
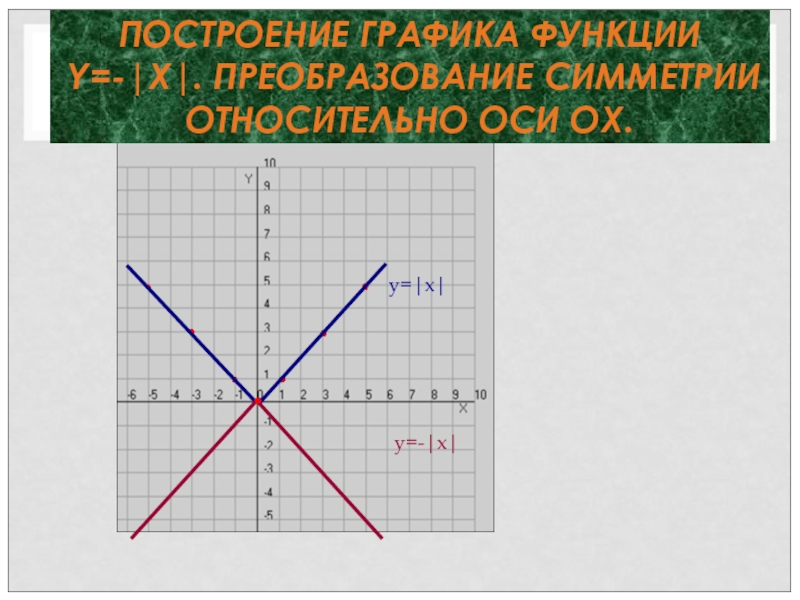
- 26. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y=-|X|. ПРЕОБРАЗОВАНИЕ СИММЕТРИИ ОТНОСИТЕЛЬНО ОСИ ОX.y=|x|y=-|x|
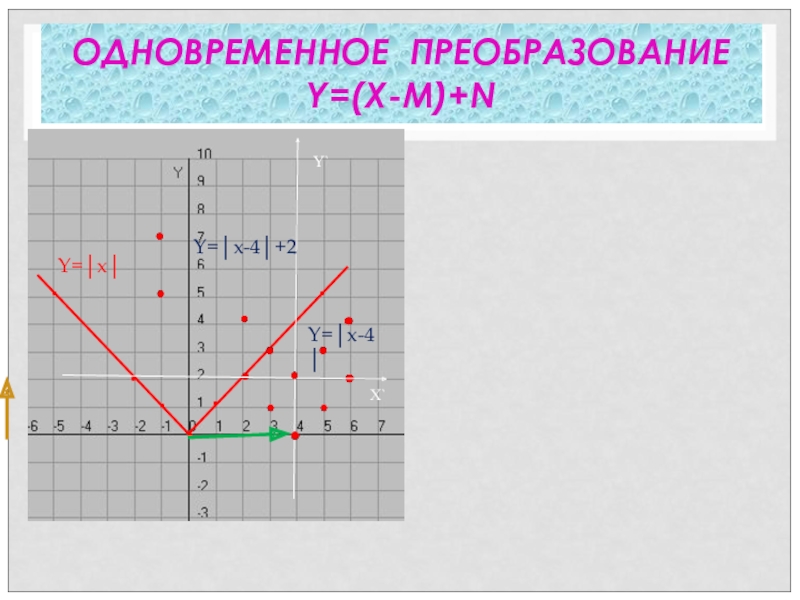
- 27. ОДНОВРЕМЕННОЕ ПРЕОБРАЗОВАНИЕ Y=(X-М)+N • • • • • • • Y=│x│Y=│x-4│Y=│x-4│+2 Y`X`
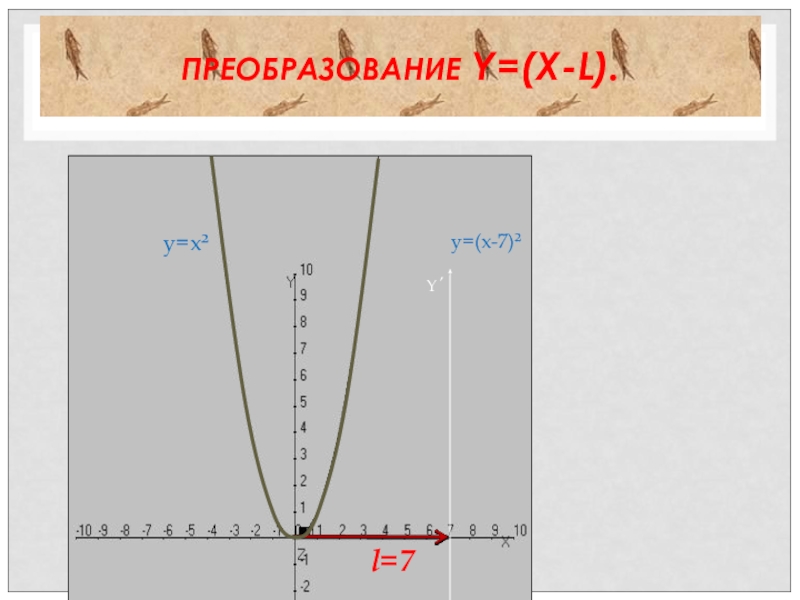
- 28. ПРЕОБРАЗОВАНИЕ Y=(X-L).y=x²y=(x-7)²Y´l=7
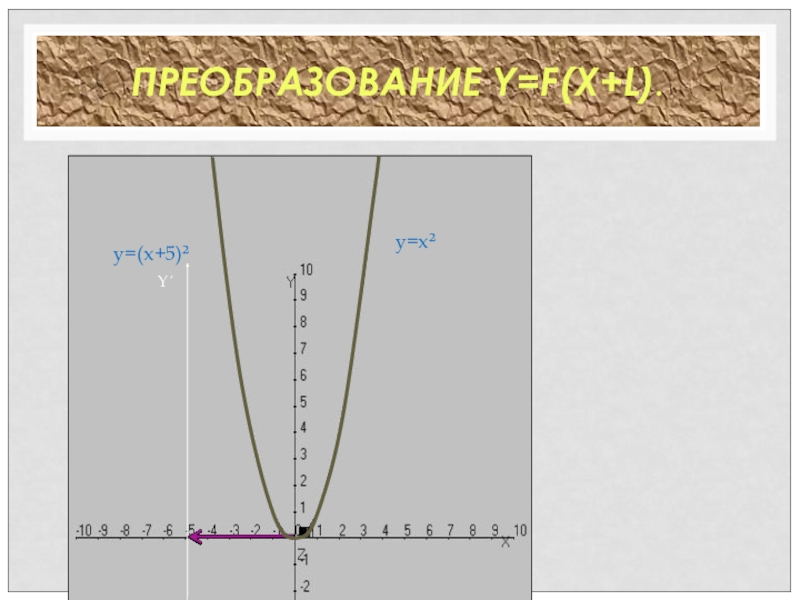
- 29. ПРЕОБРАЗОВАНИЕ Y=F(X+L).y=x²y=(x+5)²Y´
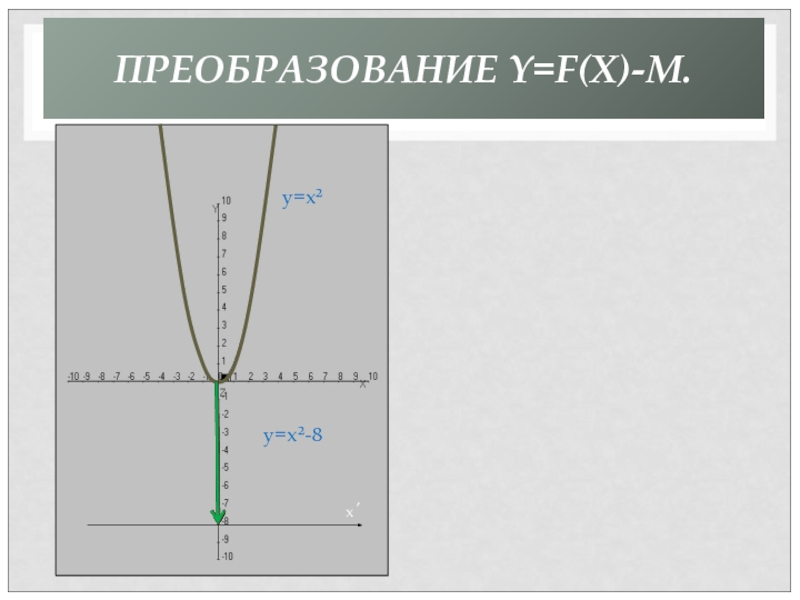
- 30. ПРЕОБРАЗОВАНИЕ Y=F(X)-M.y=x²y=x²-8x´
- 31. ПРЕОБРАЗОВАНИЕ Y=F(X)+M.y=x²y=x²+3x´
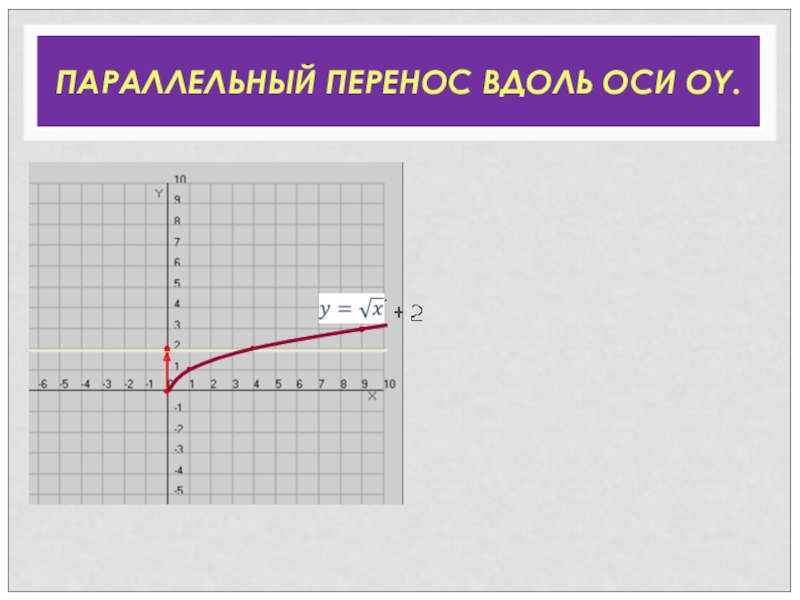
- 32. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ ОY. •
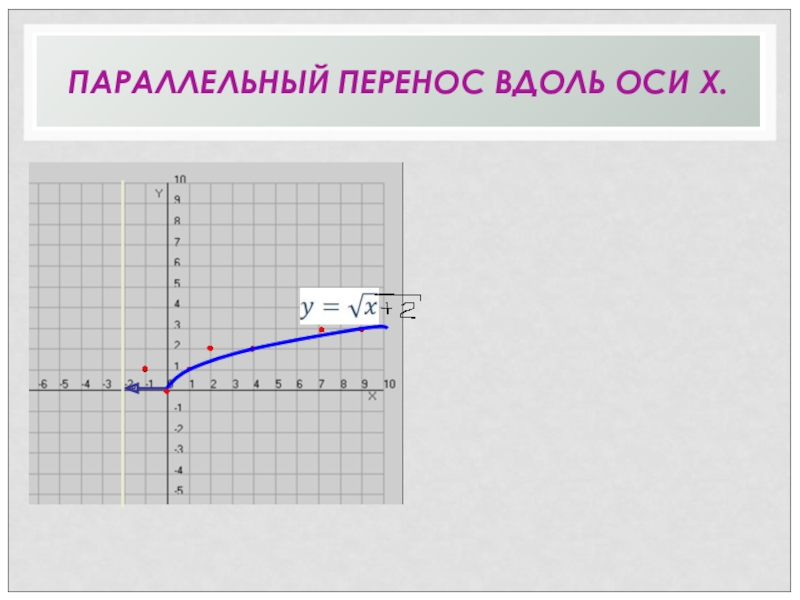
- 33. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ X. •
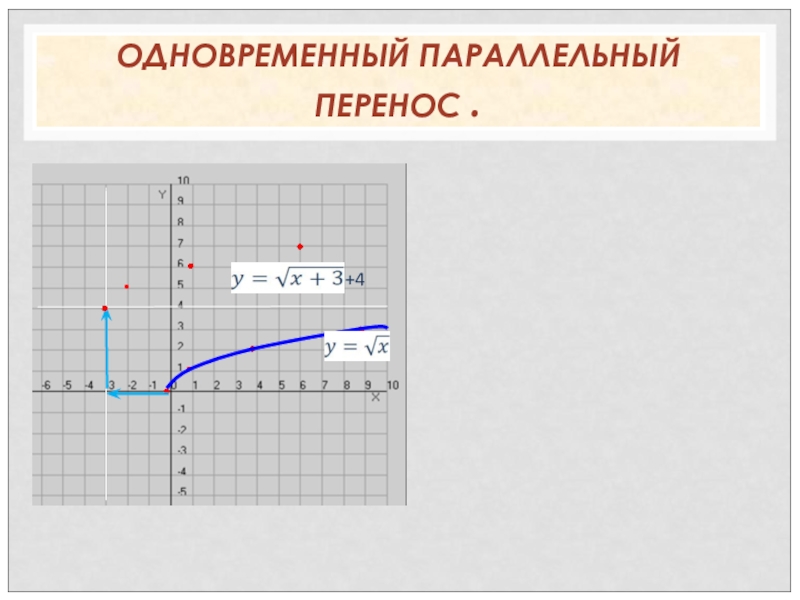
- 34. ОДНОВРЕМЕННЫЙ ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС . • •+4
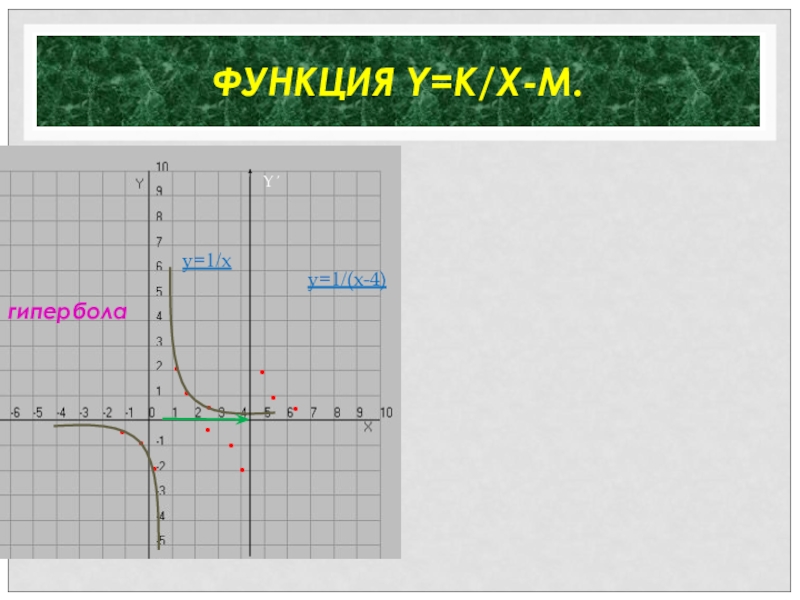
- 35. ФУНКЦИЯ Y=K/X-М. • • • •• •y=1/x
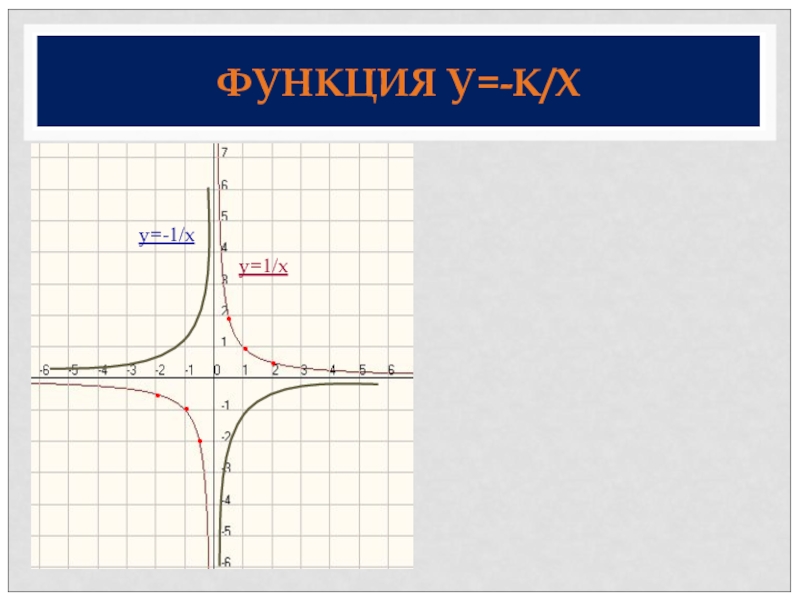
- 36. ФУНКЦИЯ У=-К/Х • • • • • •y=1/xy=-1/x
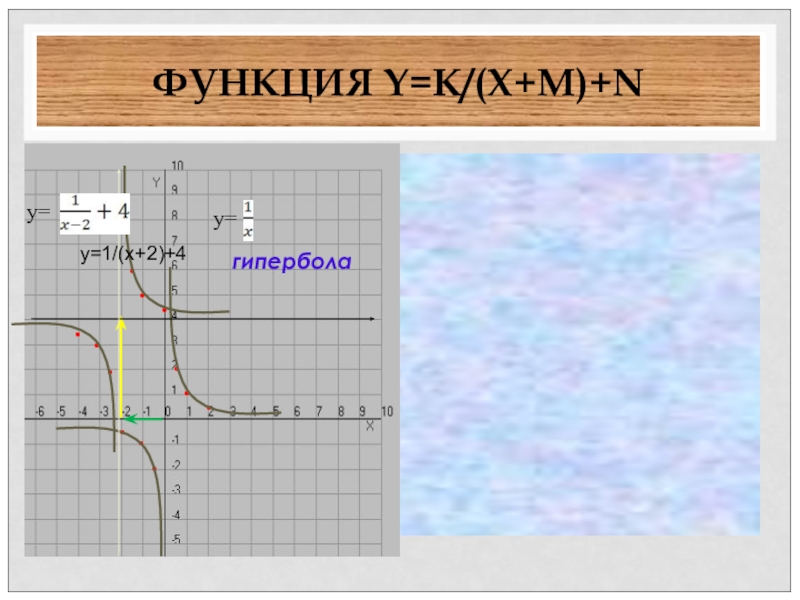
- 37. ФУНКЦИЯ Y=K/(X+М)+N • • • •• •гипербола • • • •• •y=y=у=1/(х+2)+4
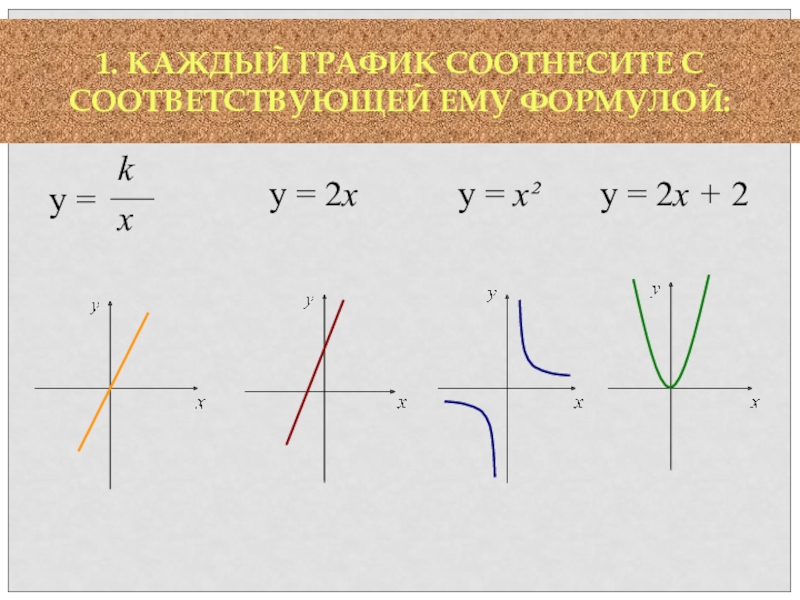
- 38. 1. КАЖДЫЙ ГРАФИК СООТНЕСИТЕ С СООТВЕТСТВУЮЩЕЙ ЕМУ
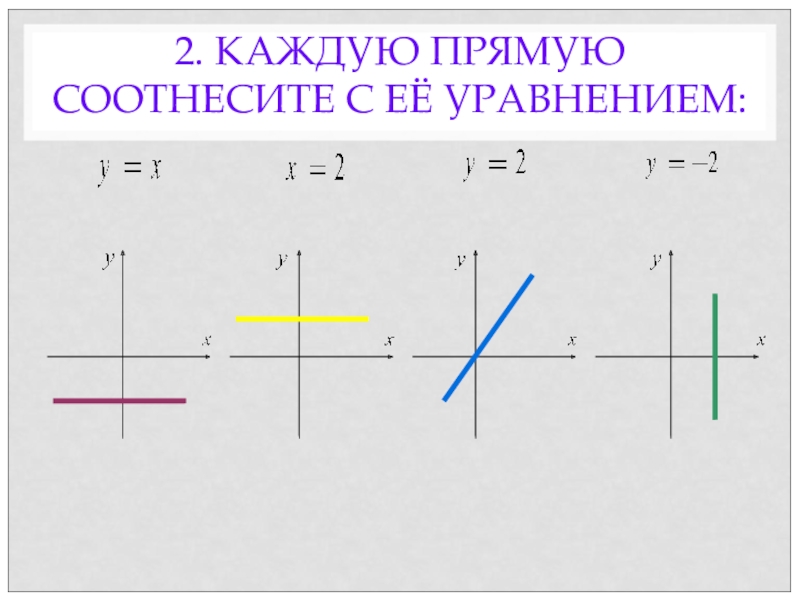
- 39. 2. КАЖДУЮ ПРЯМУЮ СООТНЕСИТЕ С ЕЁ УРАВНЕНИЕМ:
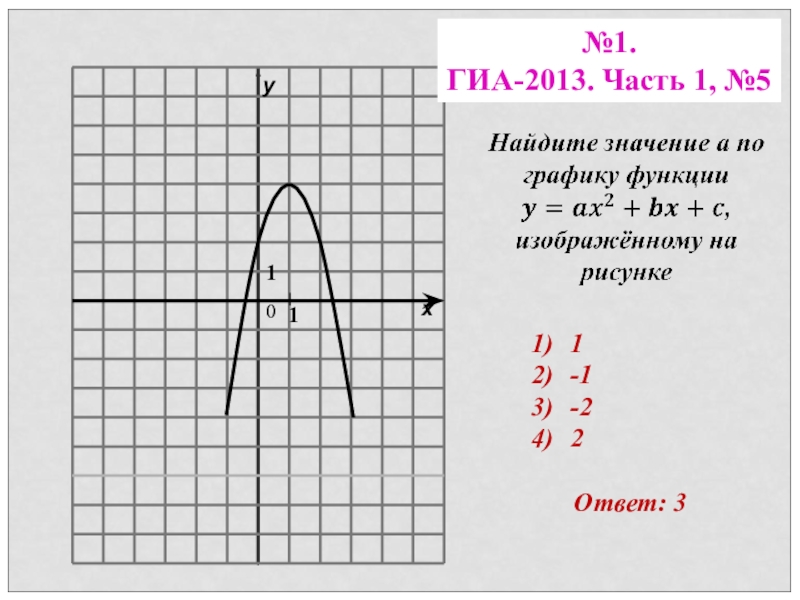
- 40. Ответ: 3
- 41. Ответ: 4
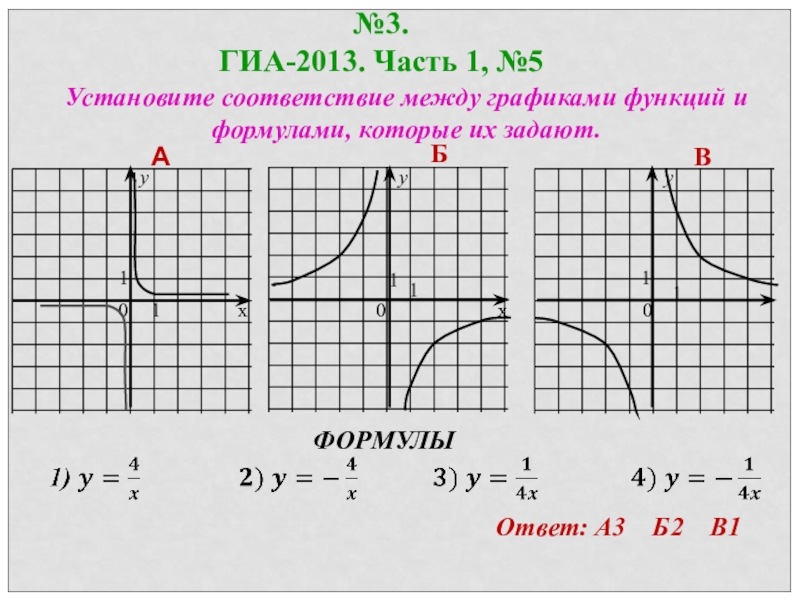
- 42. Установите соответствие между графиками функций и формулами, которые их задают.Ответ: А3 Б2 В1
- 43. З А К Л Ю Ч Е
- 44. СПИСОК ЛИТЕРАТУРЫ:
- 45. СПАСИБО ЗА ВНИМАНИЕ!
ЦЕЛЬ УРОКА: Повторить виды преобразования графиков.Научиться быстро выполнять преобразования с графиками функций: у=x², y=|x| ,y=√x, y= . Распознавать по графикамсами функции.
Слайд 1 ОБОБЩАЮЩИЙ УРОК «ПРЕОБРАЗОВАНИЯ
ГРАФИКОВ».
УЧИТЕЛЬ: ГЕЙДА И.В.
МБОУ СОШ № 108
Г. НОВОСИБИРСК
2014 ГОД
Слайд 2ЦЕЛЬ УРОКА:
Повторить виды преобразования графиков.
Научиться быстро выполнять
преобразования с графиками функций: у=x², y=|x| ,y=√x, y= .
Распознавать по графикам
сами функции.
Распознавать по графикам
сами функции.
Слайд 4Из данных функций выберите те, которые являются линейными.
А остальные? – НАЗОВИТЕ
ИХ!
у= 4 х + 2,
у = 1,5 х,
у = х + 2,5,
у = 4 х² - 5 х – 1,
у = -8 ,
у = х² + 2,5,
У = 5 х – 2,
у = -2 х,
у =
y = 3x³ - 4, x=5, y=6√x+1
Слайд 5X
Y
0
1
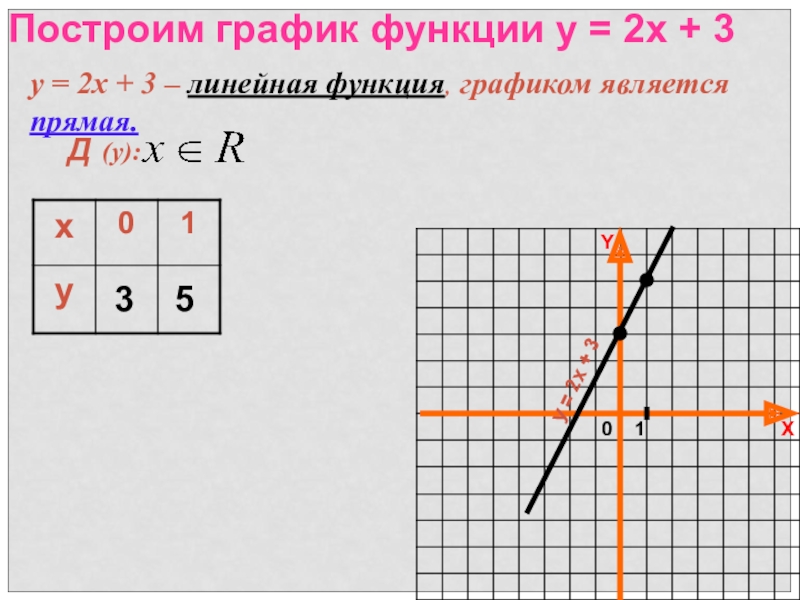
Построим график функции у = 2х + 3
у = 2х +
3 – линейная функция, графиком является прямая.
Д (у):
3
5
у = 2х + 3
Слайд 8ФУНКЦИЯ Y=X².
КВАДРАТИЧНАЯ ФУНКЦИЯ.
•
•
•
•
•
•
•
y=x²
шаблон параболы
вершина параболы
ось
симметрии параболы
Слайд 14ПРЕОБРАЗОВАНИЕ СИММЕТРИИ
ОТНОСИТЕЛЬНО ОСИ ОХ
•
•
•
•
•
•
•
y=x²
парабола
y=-x²
График
функции y= -f(x) получается из графика функции y=f(x) с помощью осевой симметрии относительно оси 0x.
.
Слайд 15ВИДЫ ПРЕОБРАЗОВАНИЙ.
Сужение и расширение вдоль оси оy
f(x) ―>k f(x), k>0
k>1,
сужение
0
0
X
y=x²
y=2x²
y=0,5 x²
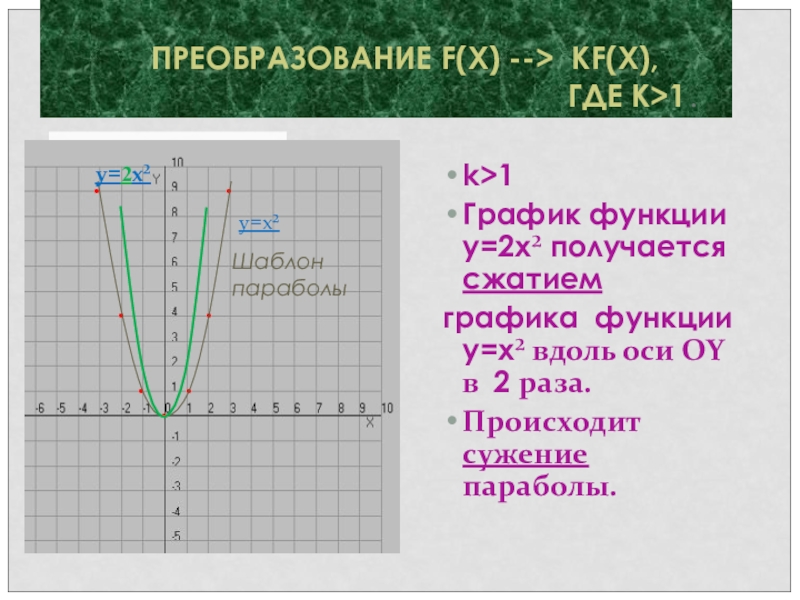
Слайд 16k>1
График функции y=2x² получается сжатием
графика функции y=x² вдоль оси ОY в
2 раза.
Происходит сужение параболы.
Происходит сужение параболы.
ПРЕОБРАЗОВАНИЕ F(X) --> KF(X),
ГДЕ K>1.
•
•
•
•
•
•
•
y=x²
Шаблон
параболы
y=2x²
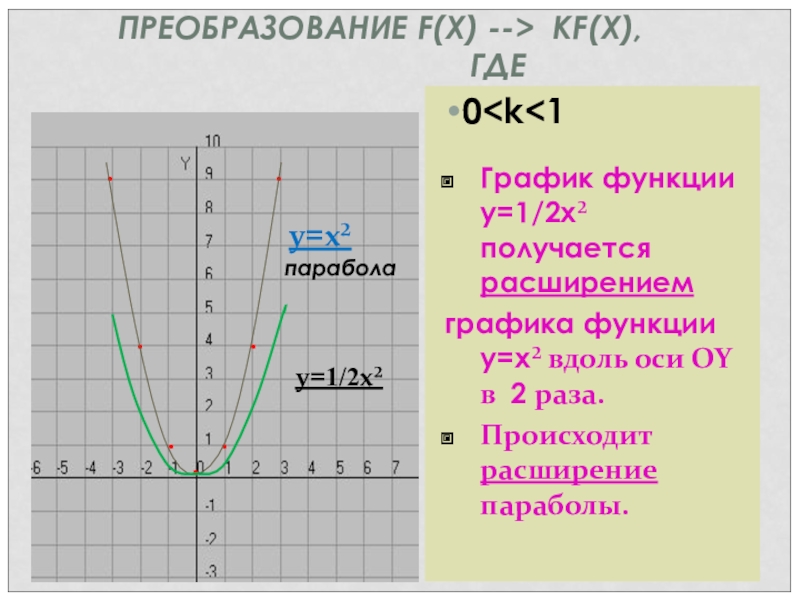
Слайд 170
ГДЕ
График функции y=1/2x² получается расширением
графика функции y=x² вдоль оси ОY в 2 раза.
Происходит расширение параболы.
•
•
•
•
•
•
•
y=x²
парабола
y=1/2x²
Слайд 42Установите соответствие между графиками функций и формулами, которые их задают.
Ответ: А3
Б2 В1
Слайд 43З А К Л Ю Ч Е Н И Е
В результате
работы мы вспомнили следующие виды преобразования графиков функций:
симметрия относительно оси оx;
симметрия относительно оси оy;
параллельный перенос вдоль оси оx и вдоль оси оy;
сжатие и растяжение вдоль оси оy,
а также комбинации данных преобразований.
Научились ставить в соответствие формулу, соответствующую данному графику.
Познакомились с новой серией задач ГИА.
симметрия относительно оси оx;
симметрия относительно оси оy;
параллельный перенос вдоль оси оx и вдоль оси оy;
сжатие и растяжение вдоль оси оy,
а также комбинации данных преобразований.
Научились ставить в соответствие формулу, соответствующую данному графику.
Познакомились с новой серией задач ГИА.
Слайд 44СПИСОК ЛИТЕРАТУРЫ:
1. А.Г. Мордкович. Алгебра-8. Учебник. М.,2009
2. Л.Э. Генденштейн и др. Наглядный справочник по алгебре и началам анализа для 7-11 классов.,1997
