- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Метод координат
Содержание
- 1. Презентация по теме Метод координат
- 2. Цели изучения метода координат Цели работы:-изучить различные
- 3. Основные виды задач №14 части 2-ой.Нахождение угла
- 4. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ Задача. В
- 5. Алгоритм решения задачи: 1.Ввести прямоугольную систему координат2.Ввести
- 6. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮЗадача. В кубе
- 7. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ Задача. В
- 8. УГОЛ МЕЖДУ ДВУМЯ ПЛОСКОСТЯМИ Задача. Дан куб
- 9. Прямоугольный параллелепипедzxyсbaA (a; 0; 0)A1 (a; 0;
- 10. Прямоугольная шестиугольная
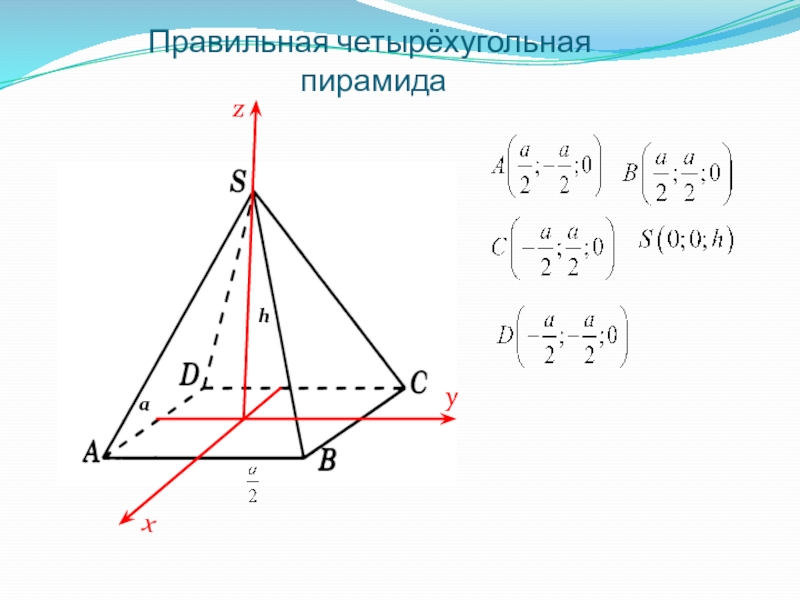
- 11. Правильная четырёхугольная пирамидаzyxah
- 12. Правильная шестиугольная пирамидаzxyC (a; 0;0)ah
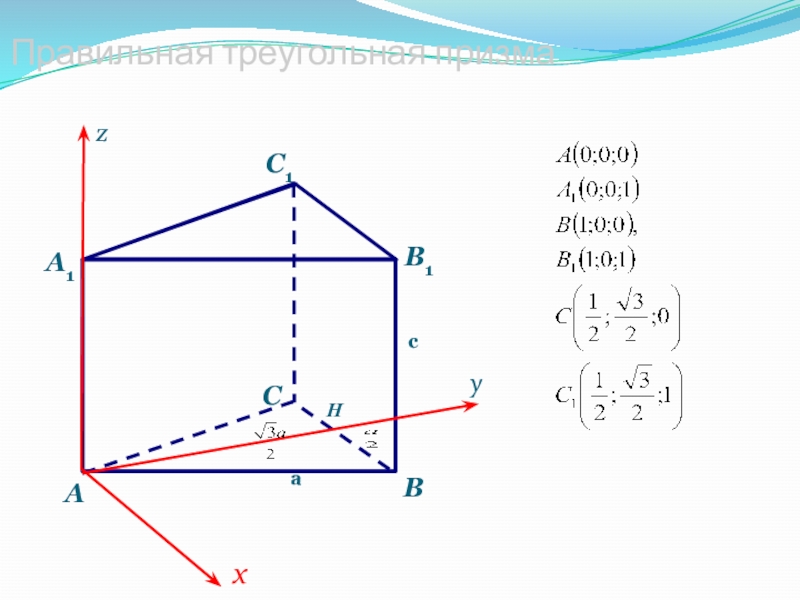
- 13. Правильная треугольная призмахуzHaс
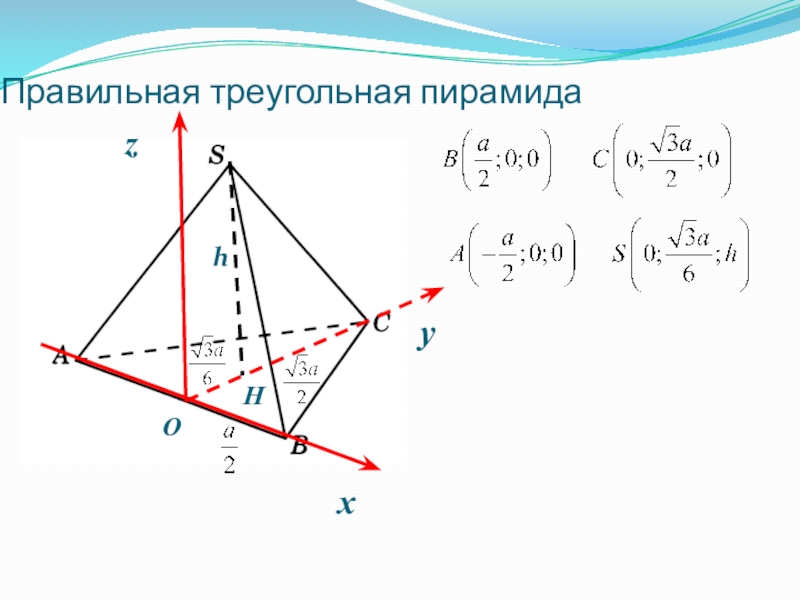
- 14. Правильная треугольная пирамидахyOzHh
- 15. плюсы и минусы использования метода координат при
- 16. Желаю успехов в выборе. Спасибо за внимание!
Слайд 1Решение стереометрических задач методом координат.
Выполнила: ученица 11 (а) класса
МБОУ «Гимназии №3»
г.
Кыдатова Ксения
Слайд 2Цели изучения метода координат
Цели работы:
-изучить различные подходы к решению задач
-выработать умение выбирать метод решения задачи в соответствии со своими математическими предпочтениями;
-повторить и закрепить различные темы и вопросы стереометрии и планиметрии, типовые стереометрические конструкции, связанные с решением текущих задач;
-развить пространственное мышление.
Слайд 3Основные виды задач №14 части 2-ой.
Нахождение угла между двумя прямыми
Нахождение угла
Нахождение расстояния от точки до плоскости
Нахождение угла между двумя плоскостями
Нахождение расстояния между двумя прямыми
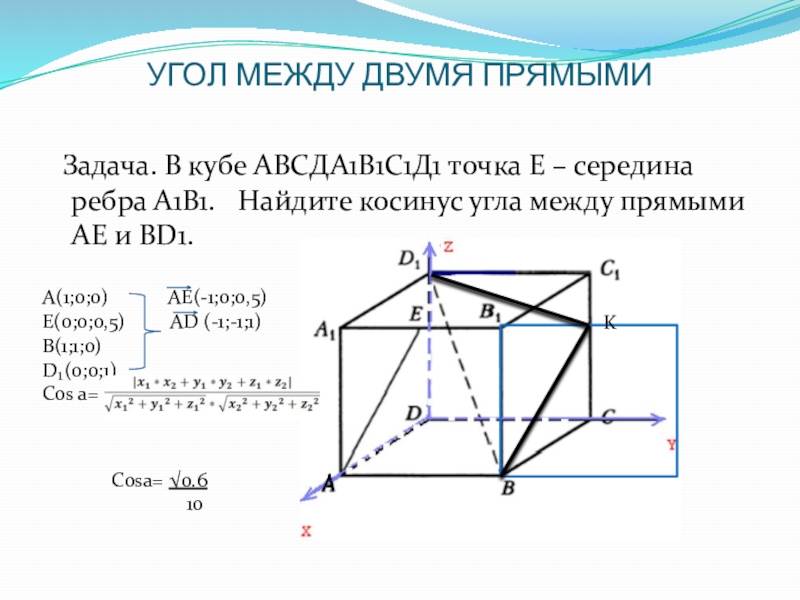
Слайд 4УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
Задача. В кубе АВСДА1В1С1Д1 точка Е –
А(1;0;0) АЕ(-1;0;0,5)
Е(0;0;0,5) АD (-1;-1;1)
В(1;1;0)
D₁(0;0;1)
Соs a=
K
Cosa= √0.6
10
Слайд 5Алгоритм решения задачи:
1.Ввести прямоугольную систему координат
2.Ввести направляющие векторы данных прямых и
3. Найти косинус угла между векторами по формуле
сosα =
Слайд 6УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Задача. В кубе АBCДА1В1С1Д1 точка Е –
1.Ввести прямоугольную систему координат
2.Ввести направляющий вектор данной прямой,
определить его координаты: АЕ (х1;у1;z1)
3.Вывести уравнение плоскости: Ах+Ву+Сz+D=0, где N (A; В; С) – вектор нормали
4.Найти синус угла между векторами по формуле:
sinα =
АE(0;0,5;1)
АС(-1;1;0) ВДД₁
Sin a= 0,5
√1,25*√2
К
О
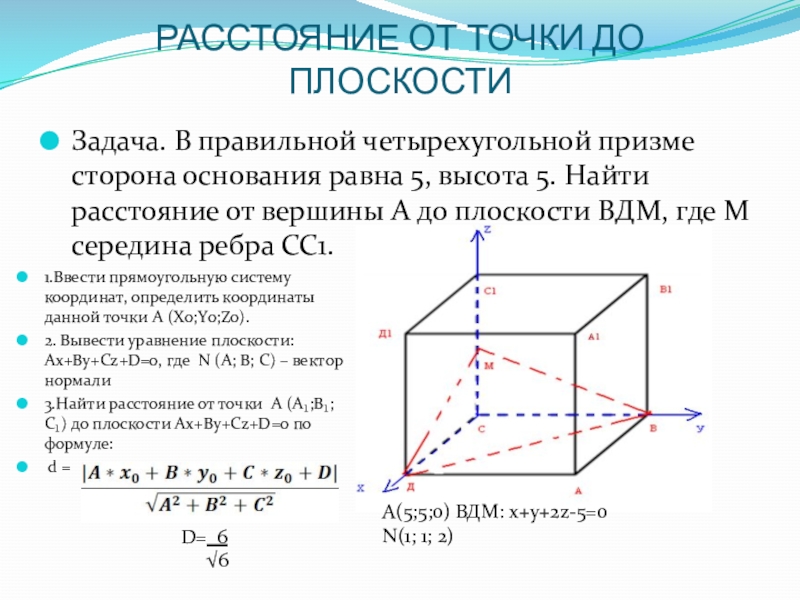
Слайд 7РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
Задача. В правильной четырехугольной призме сторона основания
1.Ввести прямоугольную систему координат, определить координаты данной точки A (Х0;Y0;Z0).
2. Вывести уравнение плоскости: Ах+Ву+Сz+D=0, где N (A; В; С) – вектор нормали
3.Найти расстояние от точки A (А₁;В₁;С₁) до плоскости Ах+Ву+Сz+D=0 по формуле:
d =
А(5;5;0) ВДМ: х+у+2z-5=0
N(1; 1; 2)
D= 6
√6
Слайд 8УГОЛ МЕЖДУ ДВУМЯ ПЛОСКОСТЯМИ
Задача. Дан куб АВСDA1B1C1D1.
Найдите угол между
1.Ввести прямоугольную систему координат.
2. Вывести уравнения плоскостей: А1х+В1у+С1z+D1=0, где
N1 (A1; В1; С1) – вектор нормали одной плоскости,
А2х+В2у+С2z+D2=0, где N2(A2; В2; С2) – вектор нормали второй плоскости.
3.Вычислите косинус угла между плоскостями по формуле:
сosα=
= 0+0+1_______= ½ =>a=60®
√0+1+1*√1+0+1
А₁В₁С: А₁(1;0;1); В₁(0;0;1)
С(0;1;0)
А1+0+С1+D=0
0+0+С1+D=0
0+B1+0+D=0
D=1;В₁=-1;С₁=-1;А₁=0
-y-z+1=0
АВ₁С₁: А(1;0;0); В₁(0;0;1)
С₁(0;1;1)
А2+0+0+D=0
0+0+C2+D=0
0+В2+С2+D=0
D=1; А2=-1; С2=-1;В2=0
-x-z+1=0
Q
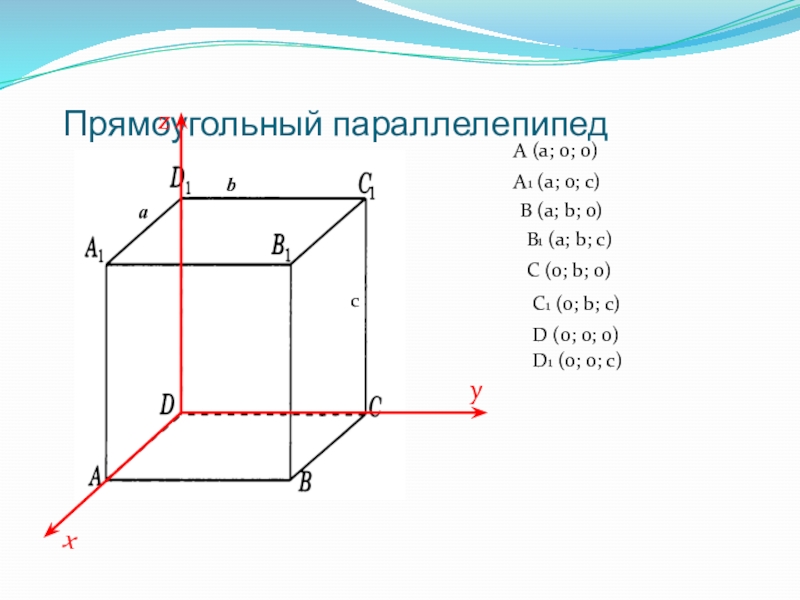
Слайд 9Прямоугольный параллелепипед
z
x
y
с
b
a
A (a; 0; 0)
A1 (a; 0; c)
B (a; b; 0)
B1
C (0; b; 0)
C1 (0; b; c)
D (0; 0; 0)
D1 (0; 0; c)
Слайд 10Прямоугольная шестиугольная
z
y
x
a
b
C
B
A
a
a
D
E
F
C(a; 0;0) C1 (a; 0;c)
F (- a; 0;0)
F1 (- a; 0;c)
Слайд 15плюсы и минусы использования метода координат при решении стереометрических задач:
ПЛЮСЫ:
Избавляет от
Нацелен на результат ЕГЭ, т.е. в рамках учебного времени, даёт возможность «натаскивания» учащихся на решение подобного типа задач.
Нет необходимости в дополнительных построениях каких-либо сечений, линейных углов, линий пересечения плоскостей. Полностью отсутствует доказательства, обоснование того или иного применения теорем стереометрии.
Экономит время и место в оформлении задачи.
Легко усваиваемый большинством учащихся с разной математической подготовкой.
МИНУСЫ:
Единственным минусом является то ,что при решении не нужна высокая степень сообразительности, что негативно сказывается на творческих способностях учащихся. -