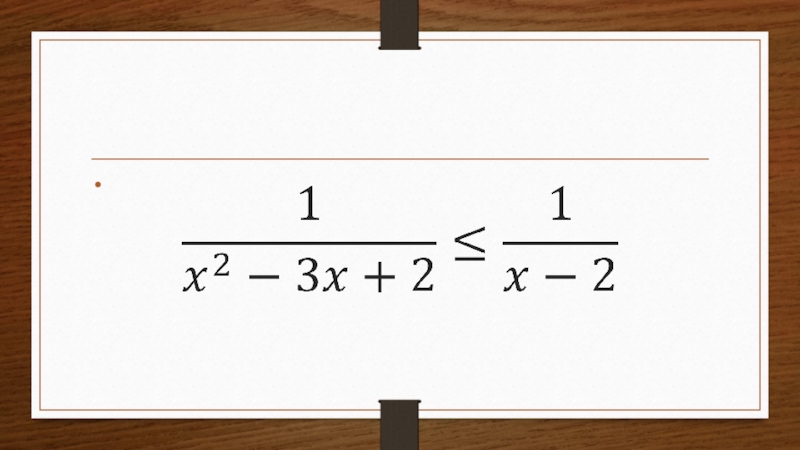- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Метод Интервалов
Содержание
- 1. Презентация по теме Метод Интервалов
- 2. Суть методаПрименяется для решения рациональных неравенств и
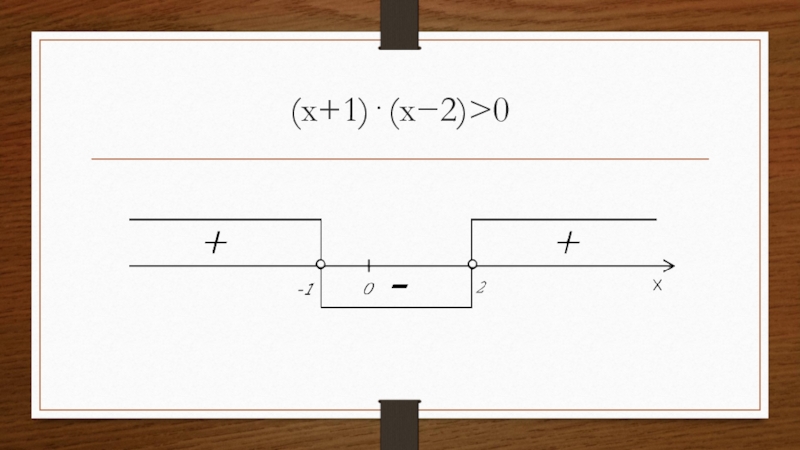
- 3. (x+1)⋅(x−2)>0Как решать, если не знаешь метод интервалов?
- 4. Нам нужно решить уравнение, оно точно такое
- 5. Что такое интервал?Это некий промежуток числовой прямой,
- 6. (x+1)⋅(x−2)>0
- 7. x∈(−∞;−1)∪(2;+∞)Круглые скобки означают, что значения, которыми ограничен
- 8. Что необходимо сделать в начале?
- 9. (x−1)⋅(x+1)⋅(x−3)
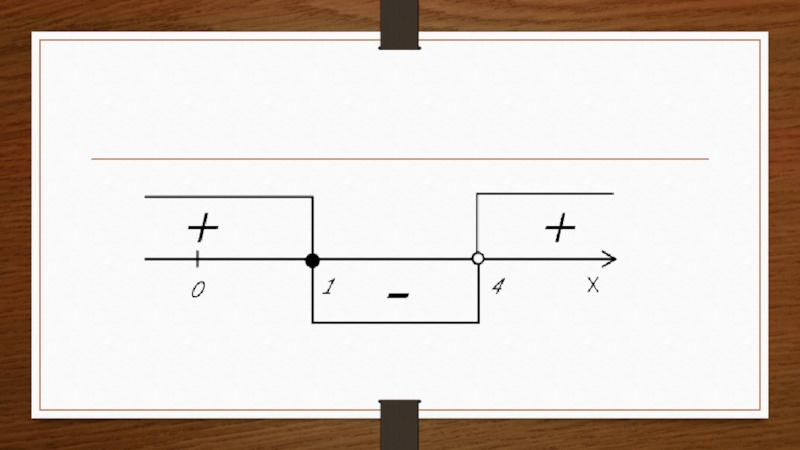
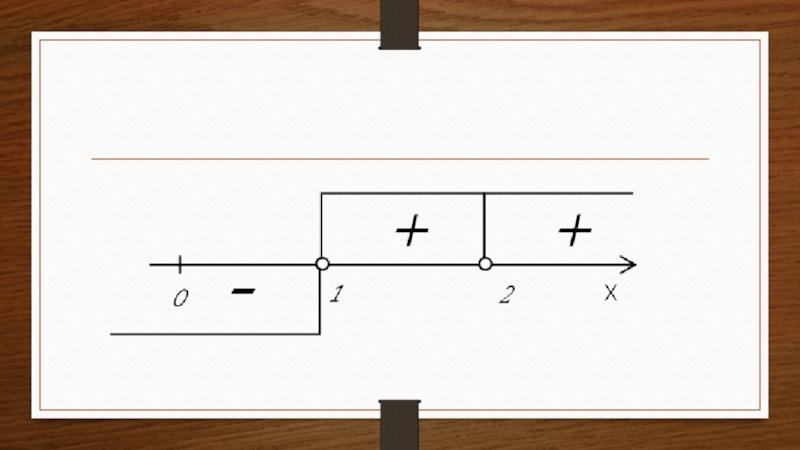
- 10. Теперь рассмотрим пример дробно-рационального неравенства – неравенство, обе части которого являются рациональными выражениями
- 11. Слайд 11
- 12. Слайд 12
- 13. План решения неравенства:Переносим всё в левую часть,
- 14. Запомни, ОДЗ превыше всего! Если все неравенство
- 15. Слайд 15
- 16. Как решать неравенства методом интервала?Переносим все в
- 17. Слайд 17
Суть методаПрименяется для решения рациональных неравенств и потому, что, зная этот метод как следует, решать эти неравенства на удивление простоСуть метода в разложении неравенства на множители (повтори тему «Разложение на множители») и определении ОДЗ и знака
Слайд 2Суть метода
Применяется для решения рациональных неравенств и потому, что, зная этот
метод как следует, решать эти неравенства на удивление просто
Суть метода в разложении неравенства на множители (повтори тему «Разложение на множители») и определении ОДЗ и знака сомножителей
Справа 0
Суть метода в разложении неравенства на множители (повтори тему «Разложение на множители») и определении ОДЗ и знака сомножителей
Справа 0
Слайд 4
Нам нужно решить уравнение, оно точно такое же как неравенство, только
вместо знака > будет знак =, корни этого уравнения и позволят определить те пограничные значения, при отступлении x от которых множители (x+1)и (x−2) будут больше или меньше нуля.
(x+1)⋅(x−2)=0
(x+1)⋅(x−2)=0
Слайд 5Что такое интервал?
Это некий промежуток числовой прямой, то есть все возможные
числа, заключенные между двумя какими-то числами – концами интервала. Эти промежутки в голове представить не так просто, поэтому интервалы принято рисовать
Слайд 7x∈(−∞;−1)∪(2;+∞)
Круглые скобки означают, что значения, которыми ограничен интервал не являются решениями
неравенства, то есть они не включены в ответ, а лишь говорят о том, что до −1−1, например, но −1−1 не есть решение.
Слайд 9(x−1)⋅(x+1)⋅(x−3)
можно определить знак в одном из интервалов, а в остальных просто чередовать знаки!
Слайд 10Теперь рассмотрим пример дробно-рационального неравенства – неравенство, обе части которого являются
рациональными выражениями
Слайд 13План решения неравенства:
Переносим всё в левую часть, справа 0.
Раскладываем на множители,
приводим к общему знаменателю.
Находим ОДЗ.
Наносим точки на ось.
Определяем знаки.
Находим ОДЗ.
Наносим точки на ось.
Определяем знаки.
Слайд 14Запомни, ОДЗ превыше всего! Если все неравенство и знаки равенства говорят
одно, а ОДЗ – другое, доверяй ОДЗ
Слайд 16Как решать неравенства методом интервала?
Переносим все в левую часть, справа оставляем
только ноль;
Находим ОДЗ;
Наносим на ось все корни неравенства;
Берем произвольный xx из одного из промежутков и определяем знак в интервале к которому относится корень, чередуем знаки, обращая внимание на корни, повторяющиеся в неравенстве несколько раз, от четности или нечетности количества раз их повторения зависит, меняется знак при прохождении через них или нет;
В ответ пишем интервалы, соблюдая выколотые и не выколотые точки (смотри ОДЗ), ставя необходимые виды скобок между ними.
Находим ОДЗ;
Наносим на ось все корни неравенства;
Берем произвольный xx из одного из промежутков и определяем знак в интервале к которому относится корень, чередуем знаки, обращая внимание на корни, повторяющиеся в неравенстве несколько раз, от четности или нечетности количества раз их повторения зависит, меняется знак при прохождении через них или нет;
В ответ пишем интервалы, соблюдая выколотые и не выколотые точки (смотри ОДЗ), ставя необходимые виды скобок между ними.