Смоленск 2019
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Магические квадраты
Содержание
- 1. Презентация по теме Магические квадраты
- 2. Проблема – магические квадраты – магические ли
- 3. Познакомиться с историей.Выяснить виды магических квадратов и
- 4. Я думаю, что существуют способы заполнения магических квадратов, изучив которые можно составить магические квадраты любого порядка.Гипотеза
- 5. Объект исследования: магический квадрат.Предмет исследования: программа.Объект и предмет исследования
- 6. АктуальностьМагические квадраты развивают интеллект детей и взрослых
- 7. Квадрат Ло-шуИстория появления Магических квадратов Возникновение магических
- 8. Пандиагональные магические квадратыВиды магических квадратов Нормальный МК -
- 9. Шифруемый текст вписывали в магические квадраты в
- 10. СудокуЭту игру, также известную как магический квадрат
- 11. ПрограммаЗа программу я взял Excel и Паскаль
- 12. Источники Википедия: https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D0%B3%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82https://studopedia.ru/17_47229_v-primenenie-magicheskih-kvadratov.htmlhttps://vuzlit.ru/836508/primenenie_magicheskih_kvadratov_sudoku_yaponskie_golovolomki#840
- 13. Спасибо за внимание
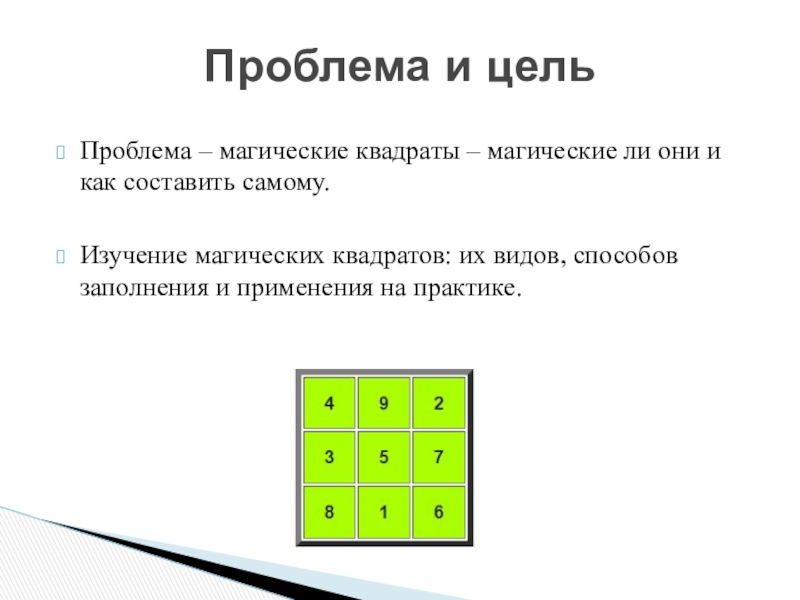
Проблема – магические квадраты – магические ли они и как составить самому.Изучение магических квадратов: их видов, способов заполнения и применения на практике.Проблема и цель
Слайд 1МАГИЧЕСКИЕ КВАДРАТЫ
Выполнил:Лексиков Денис Александрович
учащийся 10 класса А
МБОУ «СШ №34»
Руководитель: Русакова Татьяна
Николаевна»
Слайд 2Проблема – магические квадраты – магические ли они и как составить
самому.
Изучение магических квадратов: их видов, способов заполнения и применения на практике.
Изучение магических квадратов: их видов, способов заполнения и применения на практике.
Проблема и цель
Слайд 3Познакомиться с историей.
Выяснить виды магических квадратов и способы их заполнения.
Выявить применение
магических квадратов.
Создать программу для составления магических квадратов.
Создать программу для составления магических квадратов.
Задачи
Слайд 4Я думаю, что существуют способы заполнения магических квадратов, изучив которые можно
составить магические квадраты любого порядка.
Гипотеза
Слайд 5Объект исследования: магический квадрат.
Предмет исследования: программа.
Объект и предмет исследования
Слайд 6Актуальность
Магические квадраты развивают интеллект детей и взрослых в виде умных игр,
например судоку, также помогают лучше узнать цифры и развить логическое мышление.
Слайд 7Квадрат Ло-шу
История появления Магических квадратов
Возникновение магических квадратов относится к глубокой древности.
Наиболее ранние сведения о них содержатся, по-видимому, в китайских книгах, написанных в IV — V вв. до н. э. Из дошедших до нас древних магических квадратов самым «старым» является таблица Ло-шу (2200 до н. э.).
Таблица Ло-шу состоит из 9 клеток: 3 строк и 3 столбцов, заполненных натуральными числами от 1 до 9. В этом магическом квадрате суммы чисел по всем строкам, столбцам и двум диагоналям равны одному и тому же числу 15.
В Европе изображение магических квадратов впервые встречается на гравюре «Меланхолия» немецкого художника Альбрехта Дюрера (1514). Этот магический квадрат состоит из 16 клеток: 4 строк и 4 столбцов, заполненных натуральными числами от 1 до 16. В нем сумма чисел по каждой строке, каждому столбцу и двум диагоналям равна 34. Средние числа в нижней строке (15 и 14) означают дату 1514 — год издания этой гравюры А. Дюрера.
Магический квадрат — это квадратная таблица n x n, заполненная n2 числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой.
Таблица Ло-шу состоит из 9 клеток: 3 строк и 3 столбцов, заполненных натуральными числами от 1 до 9. В этом магическом квадрате суммы чисел по всем строкам, столбцам и двум диагоналям равны одному и тому же числу 15.
В Европе изображение магических квадратов впервые встречается на гравюре «Меланхолия» немецкого художника Альбрехта Дюрера (1514). Этот магический квадрат состоит из 16 клеток: 4 строк и 4 столбцов, заполненных натуральными числами от 1 до 16. В нем сумма чисел по каждой строке, каждому столбцу и двум диагоналям равна 34. Средние числа в нижней строке (15 и 14) означают дату 1514 — год издания этой гравюры А. Дюрера.
Магический квадрат — это квадратная таблица n x n, заполненная n2 числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой.
Слайд 8Пандиагональные магические квадраты
Виды магических квадратов
Нормальный МК - магический квадрат, заполненный целыми числами
от 1 до n2.
Полумагический квадрат - квадрат, заполненный числами от 1 до n2., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.
Aссоциативный, или симметричный МК, такой магический квадрат, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата.
Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.
Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.
Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.
Мультимагический квадрат - обобщение бимагических квадратов на произвольную степень n.
Полумагический квадрат - квадрат, заполненный числами от 1 до n2., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.
Aссоциативный, или симметричный МК, такой магический квадрат, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата.
Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.
Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.
Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.
Мультимагический квадрат - обобщение бимагических квадратов на произвольную степень n.
Слайд 9Шифруемый текст вписывали в магические квадраты в соответствии с нумерацией их
клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения. В те времена считалось, что созданные с помощью магических квадратов шифртексты охраняет не только ключ, но и магическая сила. Пример магического квадрата и его заполпен сообщепием:
ПРИЛЕТАЮ ВОСЬМОГО
Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вполне загадочный вид:
ОИРМ ЕОСЮ ВТАЬ ЛГОП
Пример магического квадрата и его заполнения сообщением ПРИЛЕТАЮ ВОСЬМОГО.
ПРИЛЕТАЮ ВОСЬМОГО
Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вполне загадочный вид:
ОИРМ ЕОСЮ ВТАЬ ЛГОП
Пример магического квадрата и его заполнения сообщением ПРИЛЕТАЮ ВОСЬМОГО.
Применение магических квадратов
Шифрование
Слайд 10Судоку
Эту игру, также известную как магический квадрат придумал в 1783 году
швейцарский математик Леонард Эйлер. Судоку (яп. «су» - число, «доку» - рядом, стоящее отдельно) - японские числовые головоломки, где в квадрате 9х9 клеток нужно расставить числа от 1 до 9 особым образом.
Судоку различаются по уровню сложности, которые отличаются друг от друга количеством выставленных заранее цифр.
В настоящее время судоку широко распространены за пределами Японии: их любят разгадывать как взрослые, так и дети по всему миру
Судоку различаются по уровню сложности, которые отличаются друг от друга количеством выставленных заранее цифр.
В настоящее время судоку широко распространены за пределами Японии: их любят разгадывать как взрослые, так и дети по всему миру
Слайд 11Программа
За программу я взял Excel и Паскаль и в них я
продемонстрирую составление судоку и самого магического квадрата для однозначных цифр.