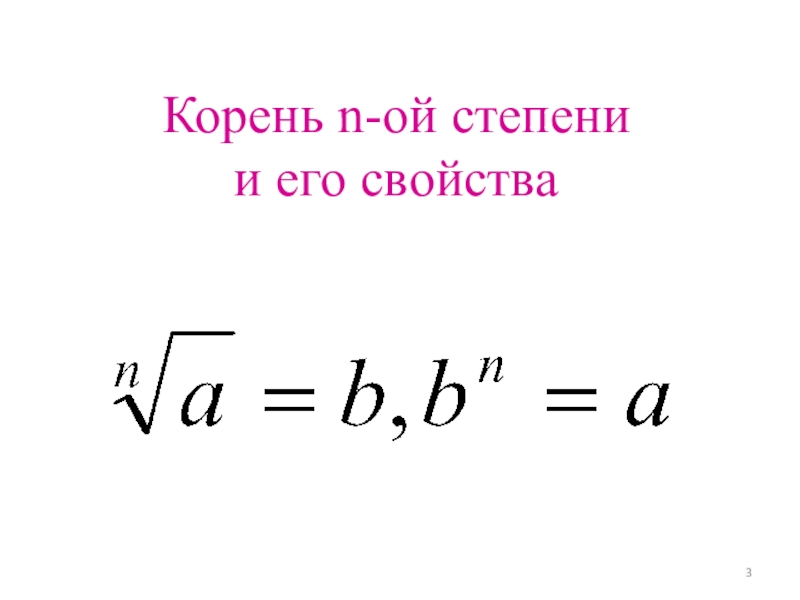- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Корень n-ой степени и его свойства
Содержание
- 1. Презентация по теме Корень n-ой степени и его свойства
- 2. Корень n-ой степени«Никогда не считай, что ты знаешь всё, что тебе уже больше нечему учиться».Н.Д. Зелинский
- 3. Корень n-ой степени и его свойства
- 4. Корень n-ой степени. Теорема1. Корень n-ой степени из
- 5. Слайд 5
- 6. Корень n-ой степени. Теорема3. Если a≥0, k – натуральное
- 7. Корень n-ой степени. Теорема 5. Если показатели корня
- 8. Корень n-ой степени. Примеры: Пример. Выполнить действия: Решение. Показатели
- 9. Слайд 9
- 10. Слайд 10
- 11. Задание №1Используя график, ответить на вопросы:1. Сколько корней имеет уравнение х5=7?2. Чему равны эти корни?
- 12. Задание №2Используя график, ответить на вопросы:График четной
- 13. Задание №3При каком значении параметра «а» уравнение
- 14. Решить уравнение
- 15. Ход решения уравненияЗамена:
- 16. Слово – Символ – Образ 1. С
- 17. Самостоятельная работаВариант 1.Вариант 2.1. Вычислите:2. Упростите выражение:
- 18. Вариант 1.Вариант 2.1. Вычислите:2. Упростите выражение:Самопроверка самостоятельной работы.
- 19. Пауза!!!
- 20. Синквейн Это стихотворение,
- 21. СИНКВЕЙН1 строка – одно существительное, выражающее главную
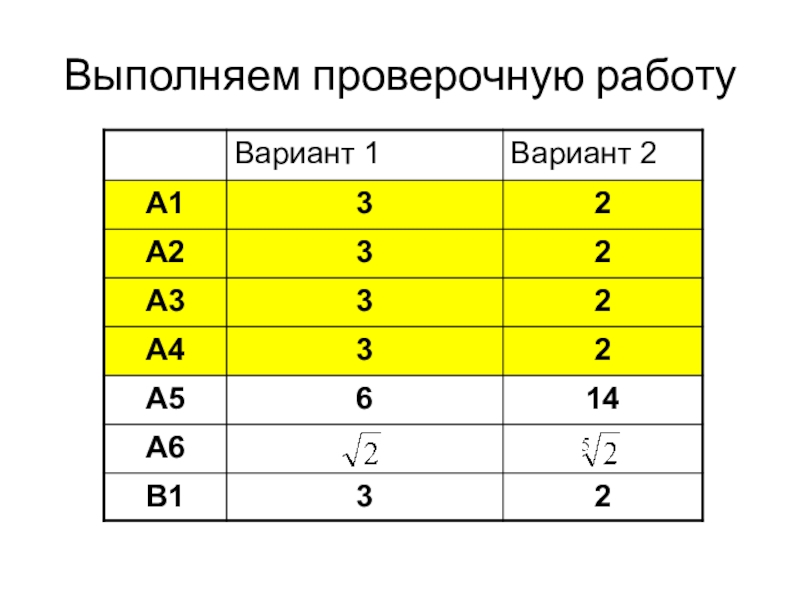
- 22. Выполняем проверочную работу
- 23. Домашнее заданиеЕсли справились полностью Изучить
- 24. Корень n-ой степени.Задачи для самостоятельного решения.Вычислить2. Вычислить3. Вычислитьа) б)Упростить:а) б) в) 5. Выполнить действия:
- 25. Всем большое спасибо за урок
Слайд 1Добро пожаловать
на урок алгебры
и начала анализа
в 11 класс
Автор:
учитель математики МБОУ СОШ № 37
города Белгорода
Слайд 2Корень n-ой степени
«Никогда не считай, что ты знаешь всё, что тебе
Н.Д. Зелинский
Слайд 4Корень n-ой степени.
Теорема1.
Корень n-ой степени из произведения двух неотрицательных чисел
Теорема 2.
Если а≥0, b>0 и n – натуральное число, большее одного тогда выполняется следующее равенство:
То есть корень n-ой степени частного равен частному корней n-ой степени.
Слайд 6Корень n-ой степени.
Теорема3.
Если a≥0, k – натуральное число и n –
Чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
Теорема4.
Если a≥0, n,k – натуральные числа, большие одного, то справедливо равенство:
Чтобы извлечь корень из корня, достаточно перемножить показатели корней.
Слайд 7Корень n-ой степени.
Теорема 5.
Если показатели корня и подкоренного выражения умножить
Слайд 8Корень n-ой степени.
Примеры:
Пример. Выполнить действия:
Решение.
Показатели корней разные числа, поэтому
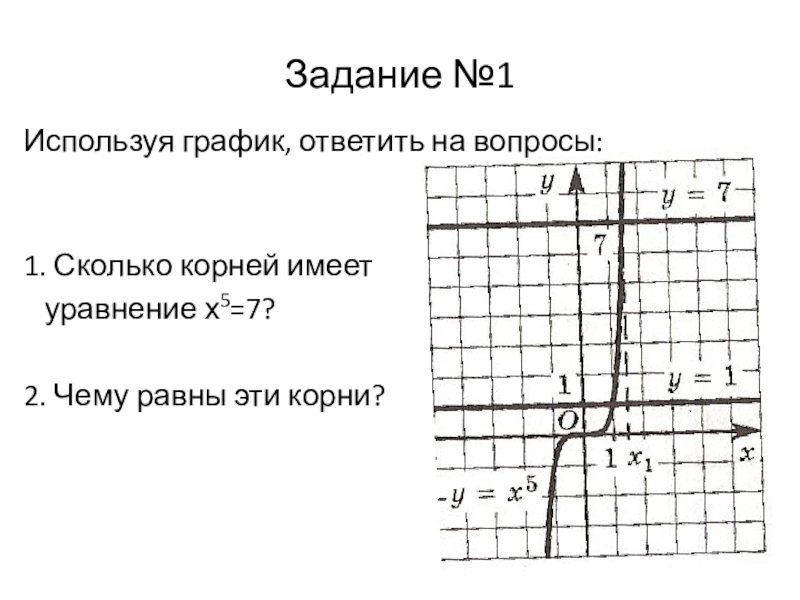
Слайд 11Задание №1
Используя график, ответить на вопросы:
1. Сколько корней имеет
2. Чему равны эти корни?
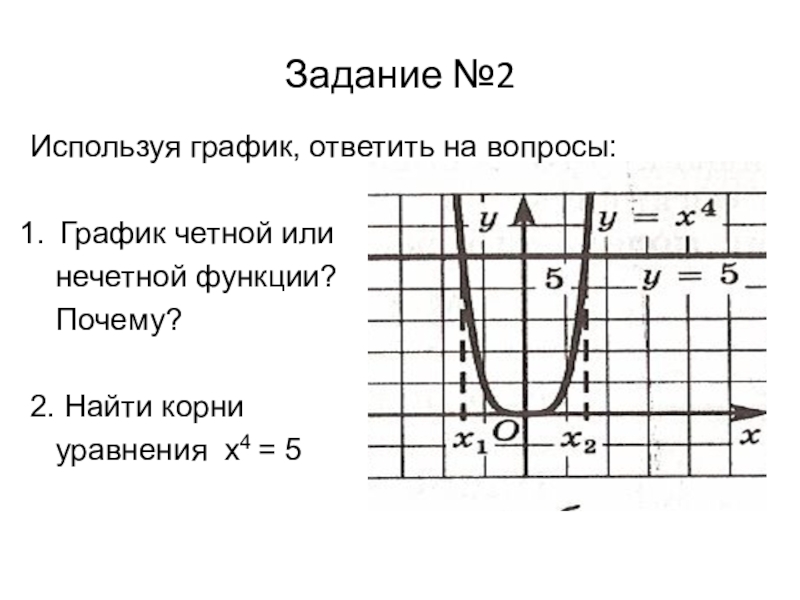
Слайд 12Задание №2
Используя график, ответить на вопросы:
График четной или
нечетной
Почему?
2. Найти корни
уравнения х4 = 5
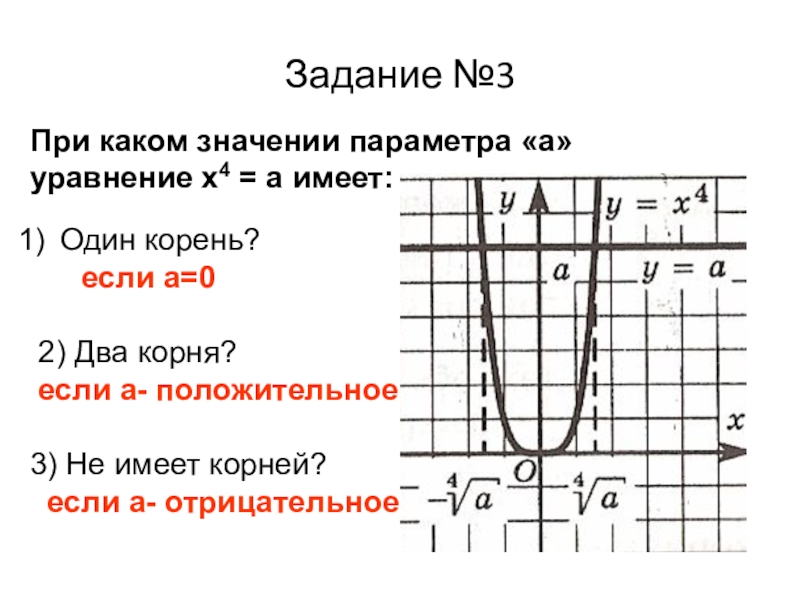
Слайд 13Задание №3
При каком значении параметра «а»
уравнение х4 = а имеет:
Один
если а=0
2) Два корня?
если а- положительное
3) Не имеет корней?
если а- отрицательное
Слайд 15Ход решения уравнения
Замена: а;
0,5а + 13
- 1,3а = - 13;
а = 10;
Обратная замена: 10;
5х = 1000;
х = 200.
Ответ: 200.
Слайд 16Слово – Символ – Образ
1. С каким математическим понятием мы
корень n–ой степени
2. Что мы применяли для вычислений корня n–ой степени
свойства корня n–ой степени
3. Сколько корней имеет уравнение хn = а, если n – нечетное число (например: х7 = 5)
один корень
4. Сколько корней имеет уравнение хn= а, если n –четное число (например: х12=а)
зависит от а:
если а – отрицательное, то нет корней;
если а = 0, то один корень;
если а – положительное, то два корня.
Слайд 18Вариант 1.
Вариант 2.
1. Вычислите:
2. Упростите выражение:
Самопроверка самостоятельной работы.
Слайд 20Синквейн
Это стихотворение, представляющее собой синтез информации
Работа над созданием синквейна развивает образное мышление.
Слайд 21СИНКВЕЙН
1 строка – одно существительное, выражающее главную тему синквейна.
2. строка –
3 строка –три глагола, описывающие действия в рамках темы.
4 строка – фраза, несущая определенный смысл.
5 строка – заключение в форме существительного (ассоциация, несущая определенный смысл)
Слайд 23Домашнее задание
Если справились полностью
Изучить пункт 33,
Выполнить №417(а,б), № 419 (а,б).
Если допущены ошибки в дополнительной части работы №394, 410 (а)
Если допущены ошибки в обязательной части работы №391-393(а,б)
Слайд 24Корень n-ой степени.
Задачи для самостоятельного решения.
Вычислить
2. Вычислить
3. Вычислить
а)
б)
Упростить:
а) б) в)
5.