- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
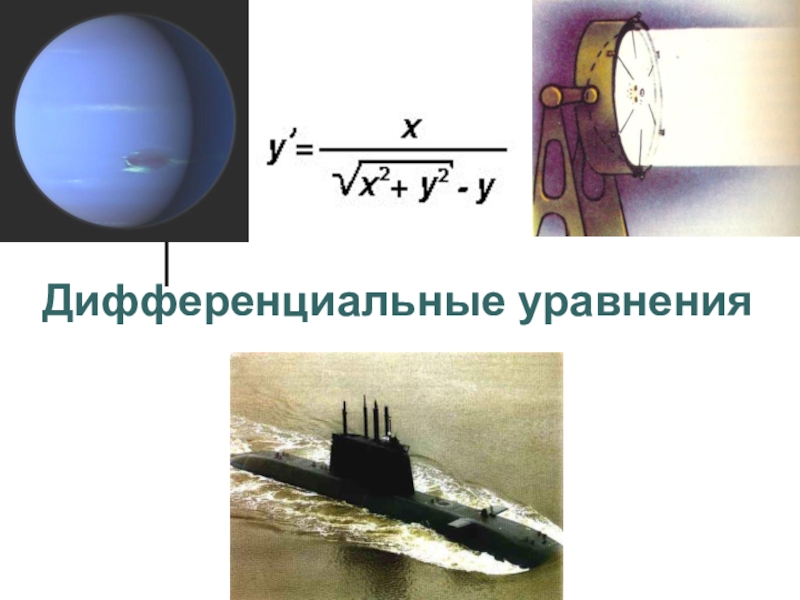
Презентация, доклад по теме Дифференциальные уравнения
Содержание
- 1. Презентация по теме Дифференциальные уравнения
- 2. Математика характеризуется как метод проникновения
- 3. Теория дифференциальных уравнений имеет свои особенности.
- 4. Первая особенность теории дифференциальных уравнений непосредственная связь теории дифференциальных уравнений с приложениями.
- 5. связь с другими разделами математики, такими, как
- 6. Необходимость решать дифференциальные уравнения возникли из нужд
- 7. ОТКРЫТИЕ ПЛАНЕТЫ НЕПТУН
- 8. Нептун - восьмая по счету (и последняя)
- 9. нептун
- 10. Вид Нептуна с Тритона
- 11. В настоящее время важную роль в развитии
- 12. дифференциальное уравнениеЭто соотношение между независимой переменной, неизвестной функцией и ее производными до некоторого порядка.
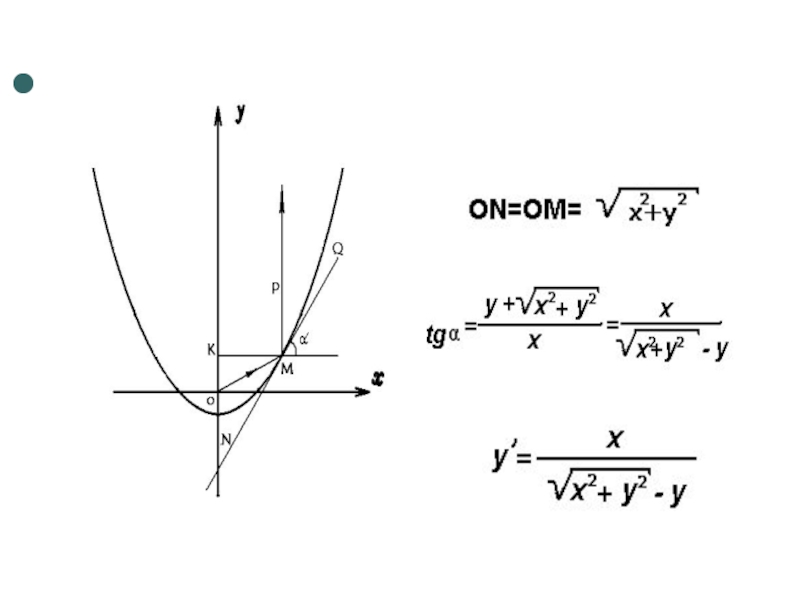
- 13. ЗАДАЧА Найти такую форму зеркала, чтобы лучи
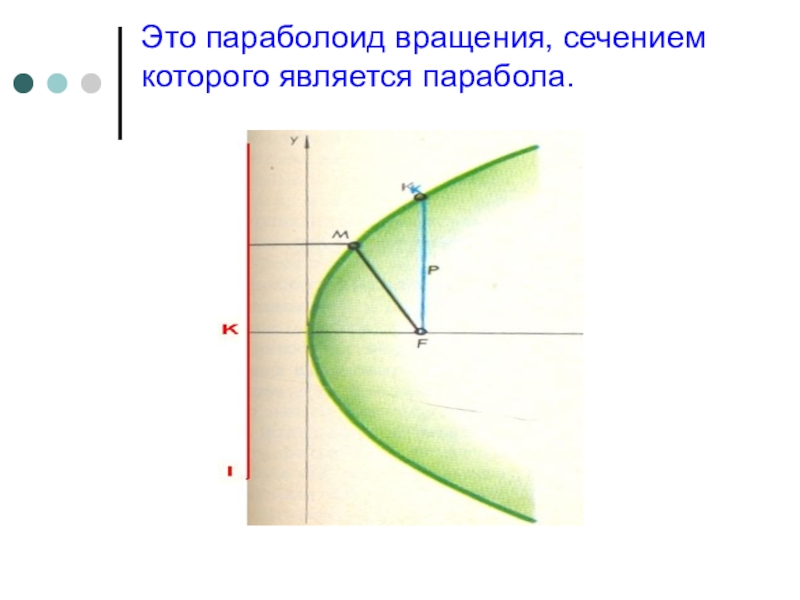
- 14. Это параболоид вращения, сечением которого является парабола.
- 15. Слайд 15
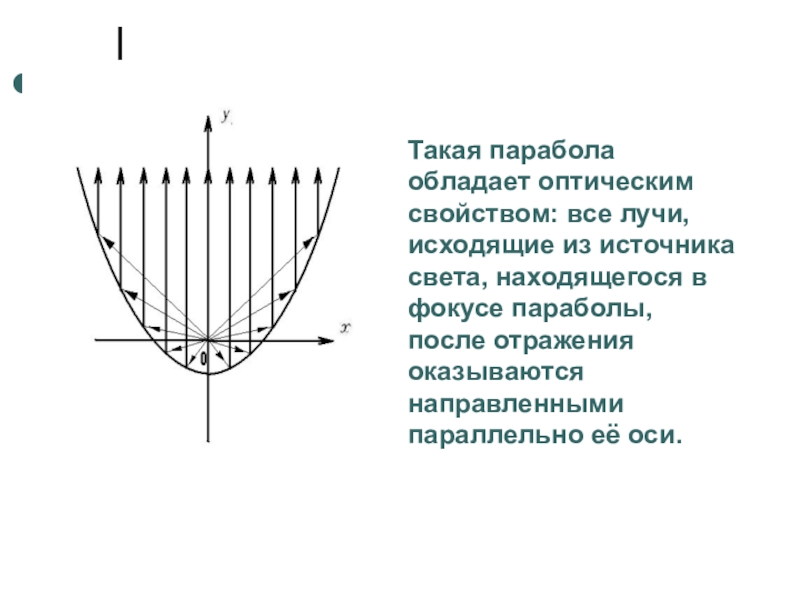
- 16. Такая парабола обладает оптическим свойством: все лучи,
- 17. Это свойство параболы используется при изготовлении прожекторов,
- 18. Задача о всплытии подводной лодки.
- 19. Под словами математическая модель всплытия подводной лодки
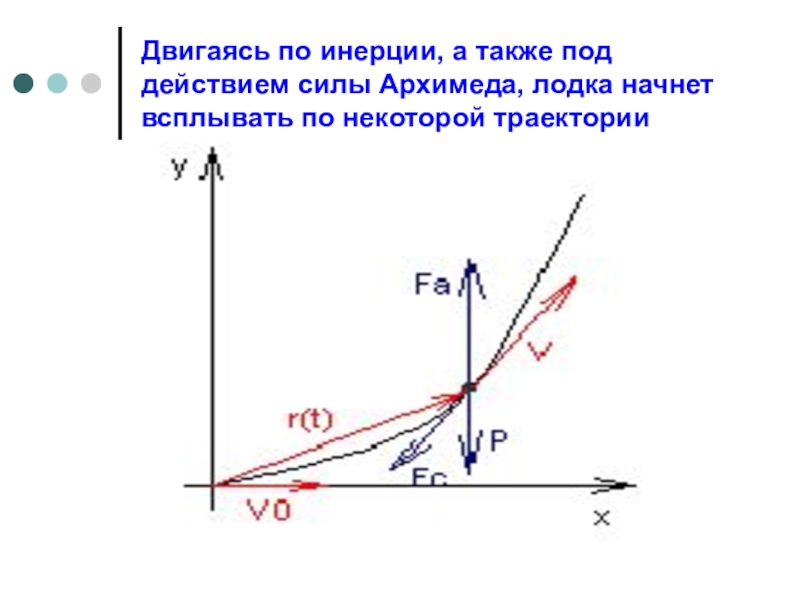
- 20. Двигаясь по инерции, а также под действием силы Архимеда, лодка начнет всплывать по некоторой траектории
- 21. Векторные уравнение в проекциях на оси Х
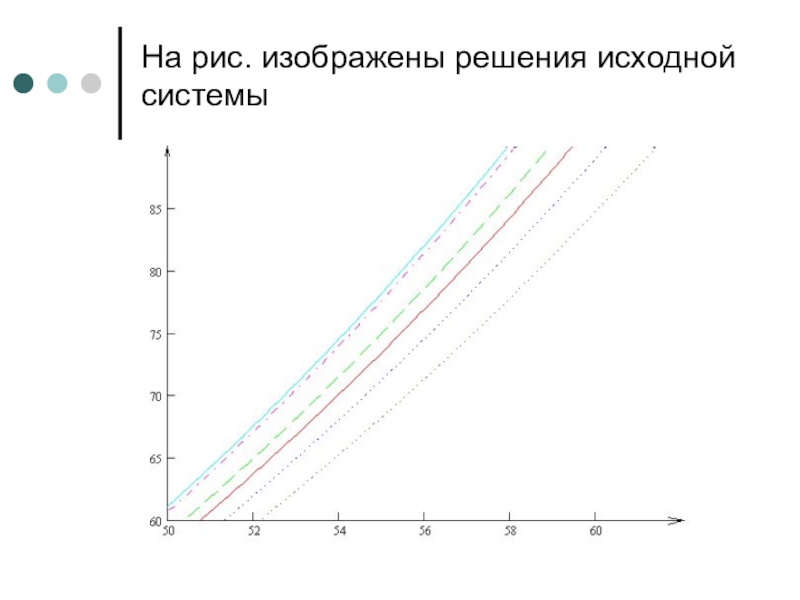
- 22. На рис. изображены решения исходной системы
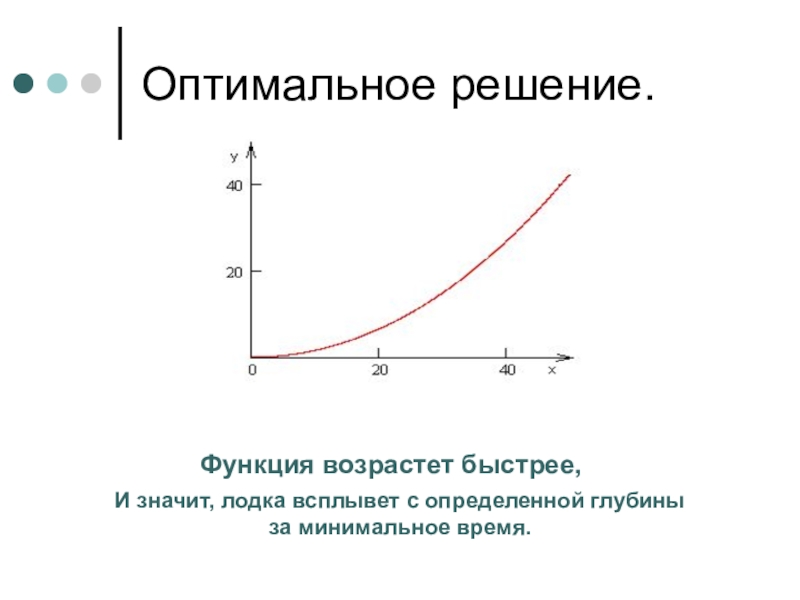
- 23. Оптимальное решение.Функция возрастет быстрее,И значит, лодка всплывет с определенной глубины за минимальное время.
- 24. Многие разделы теории
Математика характеризуется как метод проникновения в тайны природы. Основной путь применения этого метода - формирование и изучение математических моделей реального мира.
Слайд 2
Математика характеризуется как метод проникновения в тайны
природы.
Основной путь применения этого метода - формирование и изучение математических моделей реального мира.
Слайд 4
Первая особенность теории дифференциальных уравнений
непосредственная связь теории дифференциальных уравнений с
приложениями.
Слайд 5связь с другими разделами математики,
такими, как функциональный анализ,
алгебра и
теория вероятностей.
Вторая особенность теории
дифференциальных уравнений
Слайд 6Необходимость решать дифференциальные уравнения возникли из нужд механики. В небесной механике
оказалось возможным не только получить и объяснить уже известные факты, но и сделать новые открытия.
Необходимость решать дифференциальные уравнения возникли из нужд механики. В небесной механике оказалось возможным не только получить и объяснить уже известные факты, но и сделать новые открытия.
Слайд 8Нептун - восьмая по счету
(и последняя) планета от Солнца и,
как и Юпитер, Уран и Сатурн, принадлежит к семейству молодых газообразных планет.
Она был открыта в 1846 году, французским ученым Леверье.
Она был открыта в 1846 году, французским ученым Леверье.
Слайд 11В настоящее время важную роль в развитии теории дифференциальных уравнений играет
применение современных электронных вычислительных машин. Теория должна дать в руки инженера и физика методы экономного и быстрого вычисления решения.
Слайд 12дифференциальное уравнение
Это соотношение между независимой переменной, неизвестной функцией и ее производными
до некоторого порядка.
Слайд 13
ЗАДАЧА
Найти такую форму зеркала, чтобы
лучи от точечного источника света
после отражения
в нем образовали
параллельный пучок.
параллельный пучок.
Слайд 16Такая парабола обладает оптическим свойством: все лучи, исходящие из источника света,
находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси.
Слайд 17Это свойство параболы используется при изготовлении прожекторов,
телескопов, автомобильных фар, карманных
фонариков, зеркала которых имеют вид параболоидов вращения.
Слайд 19Под словами математическая модель всплытия подводной лодки подразумевается описание физического процесса,
происходящего при её всплытии с некоторой глубины.
Слайд 20Двигаясь по инерции, а также под действием силы Архимеда, лодка начнет
всплывать по некоторой траектории
Слайд 21Векторные уравнение в проекциях на оси Х и У
В проекции на
ось Х :
В проекции на ось У :
В результате получим систему дифференциальных уравнений:
В проекции на ось У :
В результате получим систему дифференциальных уравнений:
Слайд 23Оптимальное решение.
Функция возрастет быстрее,
И значит, лодка всплывет с определенной глубины
за
минимальное время.
Слайд 24 Многие разделы теории дифференциальных уравнений так разрослись,
что стали самостоятельными науками. Можно сказать, что большая часть путей, связывающих абстрактные математические теории и естественнонаучные приложения, проходит через дифференциальные уравнения. Все это обеспечивает теории дифференциальных уравнений почетное место в современной науке.