- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Числовые множества
Содержание
- 1. Презентация по теме Числовые множества
- 2. Множества чисел, принятые в математикеНатуральные числаЦелые числаРациональные числаИррациональные числаДействительные числаКомплексные числа
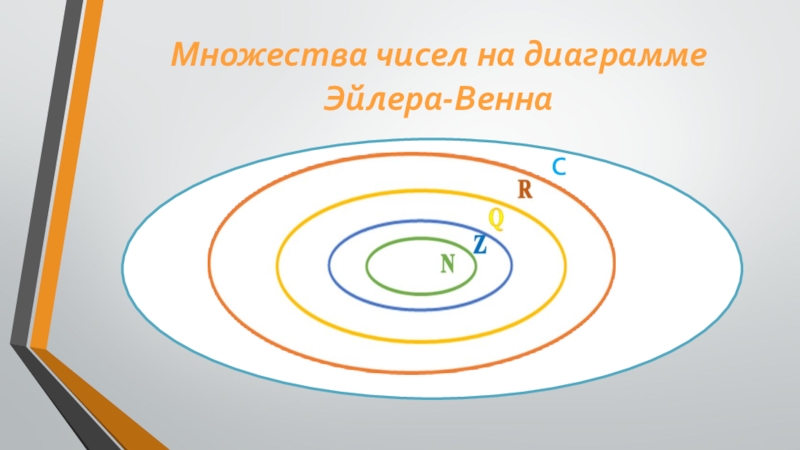
- 3. Множества чиселМножества чисел на диаграмме Эйлера-ВеннаС
- 4. Натуральные числа (N)Это числа, которые используются при счете предметов: 1, 2, 3, 4, 5, …
- 5. ЗАДАНИЕ 1. Запишите в тетради:
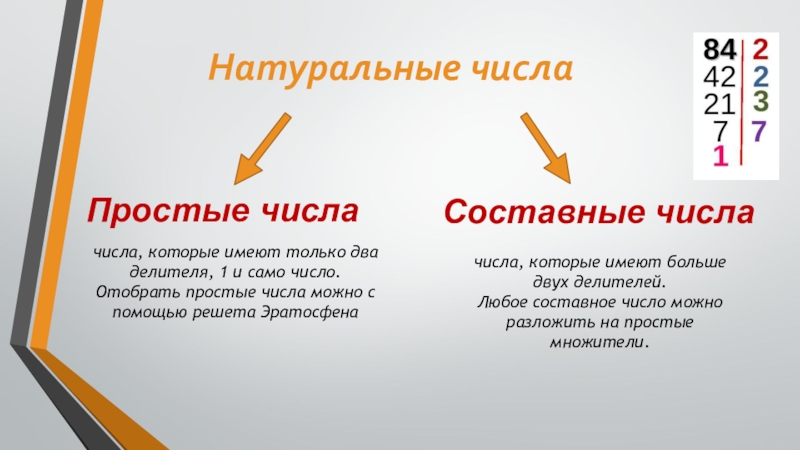
- 6. Натуральные числаПростые числаСоставные числачисла, которые имеют только
- 7. Слайд 7
- 8. ЗАДАНИЕ 2. Разложите на простые множители
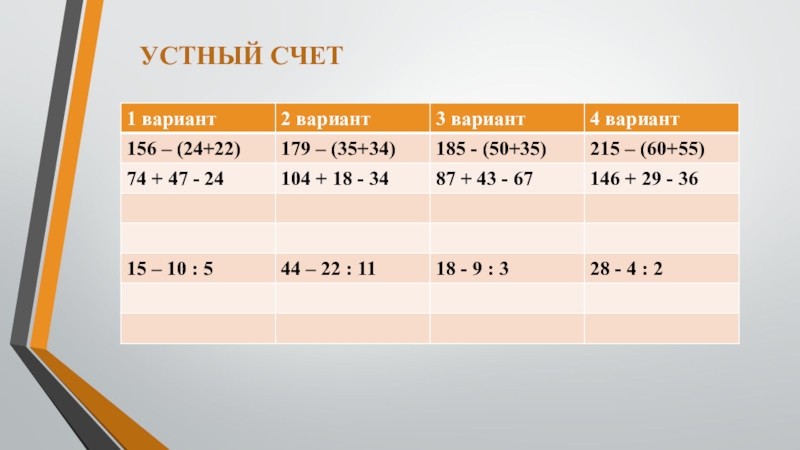
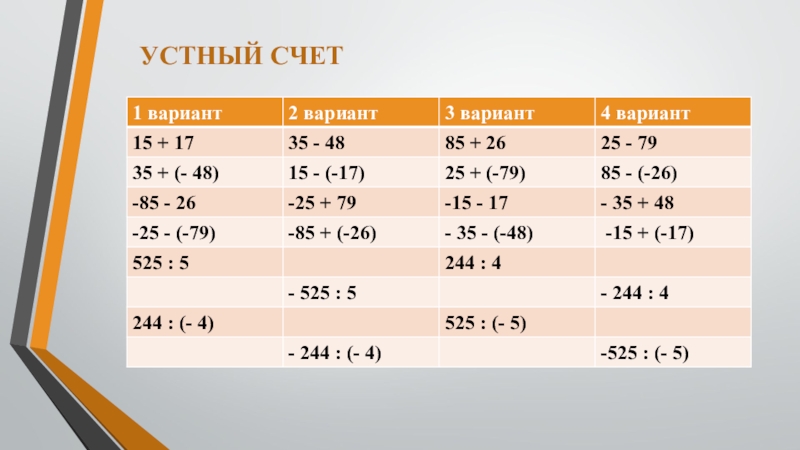
- 9. УСТНЫЙ СЧЕТ
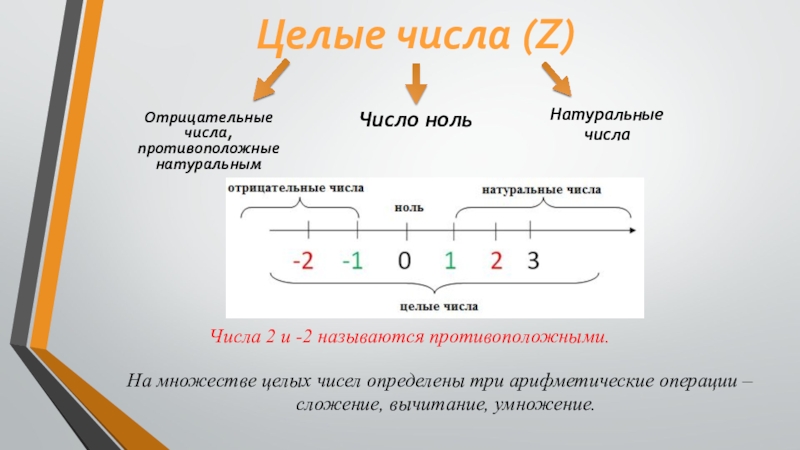
- 10. Целые числа (Z)Отрицательные числа, противоположные натуральнымЧисло нольНатуральные
- 11. ЗАДАНИЕ 3. Как изменится число,
- 12. Мнемоническое правило умножения Действия с целыми числами
- 13. УСТНЫЙ СЧЕТ
- 14. Модуль числа - это расстояние от нуля до точки, изображающей число.
- 15. ЗАДАНИЕ 4.
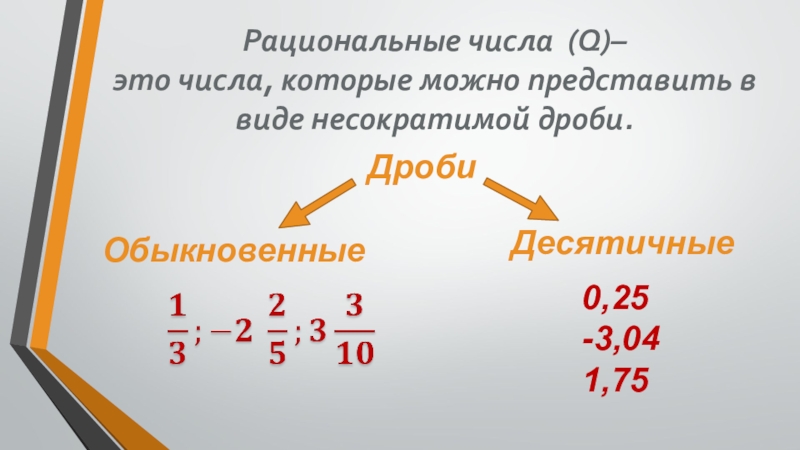
- 16. Рациональные числа (Q)– это числа, которые можно представить в виде несократимой дроби.ОбыкновенныеДесятичныеДроби0,25-3,041,75
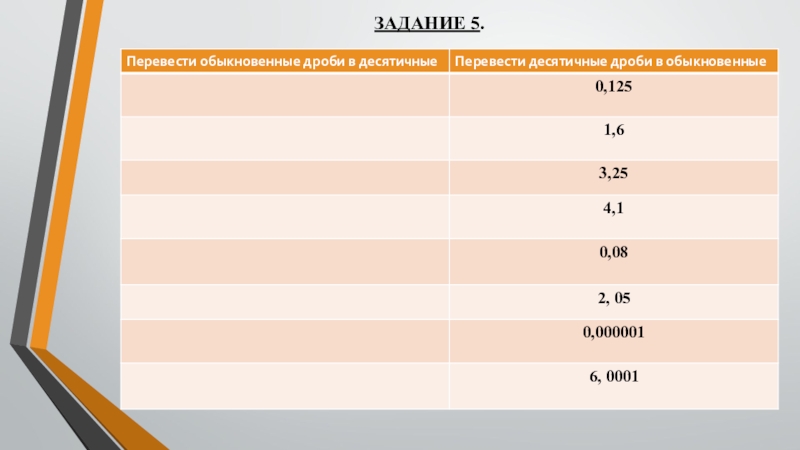
- 17. ЗАДАНИЕ 5.
- 18. ЗАДАНИЕ 6.
- 19. УСТНЫЙ СЧЕТ
- 20. Действительные числа (R)Рациональные числа (Q) –это числа,
- 21. Самые известные иррациональные числа
- 22. Самые известные иррациональные числа
- 23. Экспонента – число Эйлера или число Неппера.
- 24. ЗАДАНИЕ 7.
- 25. ЗАДАНИЕ 8.
- 26. Приближенные вычисленияПРИМЕНЕНИЕЗапись результатов измеренийРациональные и иррациональные числаАрифметические операции с различными числами
- 27. Приближенные вычисления применяются для записи результатов измеренийМасса
- 28. Приближенные вычисления применяются для сравнения рациональных и
- 29. Приближенные вычисления применяются для выполнения арифметических операций с числами
- 30. Округлить число – значит сохранить в нем
- 31. Абсолютная погрешность – это модуль разности между точным и приближенным значением. Найти абсолютную погрешность приближенных значений:
- 32. Абсолютная погрешность – это модуль разности между точным и приближенным значением.Найти абсолютную погрешность приближенных значений:
- 33. Относительная погрешность – это отношение абсолютной погрешности
- 34. Относительная погрешность – это отношение абсолютной погрешности
- 35. Арифметические операции с приближенными значениями:Правило 1. При
- 36. Арифметические операции с приближенными значениями:Правило 2. При
- 37. Арифметические операции с приближенными значениями:Правило 3. При
- 38. Арифметические операции с приближенными значениями:Правило 4. При
- 39. Арифметические операции с приближенными значениями:
- 40. Арифметические операции с приближенными значениями:
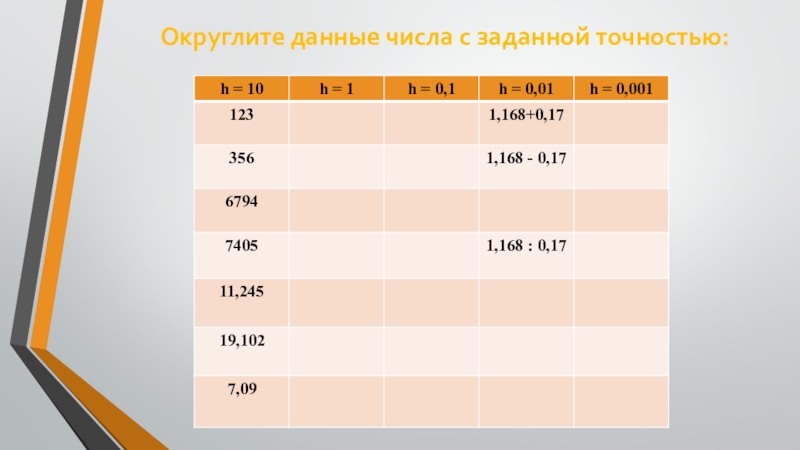
- 41. Округлите данные числа с заданной точностью:
- 42. Комплексные числа (С)
- 43. Действия с комплексными числами
- 44. Арифметические операции с комплексными числами:
Множества чисел, принятые в математикеНатуральные числаЦелые числаРациональные числаИррациональные числаДействительные числаКомплексные числа
Слайд 2Множества чисел, принятые в математике
Натуральные числа
Целые числа
Рациональные числа
Иррациональные числа
Действительные числа
Комплексные числа
Слайд 5
ЗАДАНИЕ 1. Запишите в тетради:
Самое маленькое двухзначное число?
Самое большое
двухзначное число?
Самое маленькое трехзначное?
Самое большое трехзначное?
Самое маленькое трехзначное?
Самое большое трехзначное?
Число, следующее за числом 99?
Число, предшествующее числу 300?
Число, следующее за числом 19 999?
Число, предшествующее числу 1200?
Число на 1 меньше 700?
Число на 1 больше 8 999?
Слайд 6Натуральные числа
Простые числа
Составные числа
числа, которые имеют только два делителя, 1 и
само число.
Отобрать простые числа можно с помощью решета Эратосфена
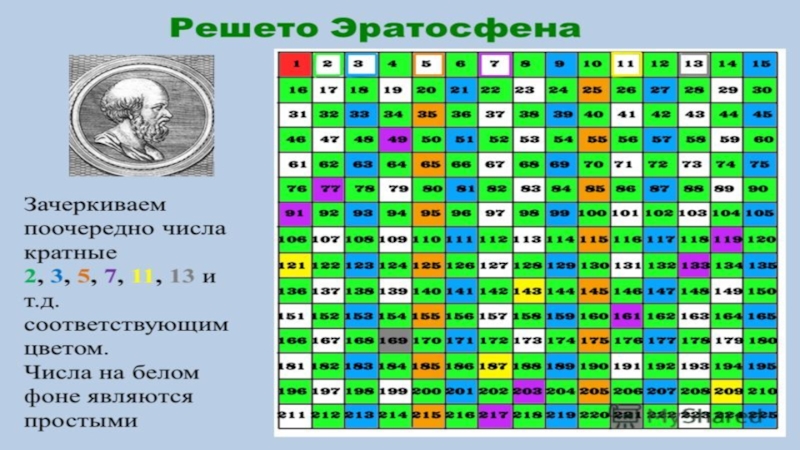
Отобрать простые числа можно с помощью решета Эратосфена
числа, которые имеют больше двух делителей.
Любое составное число можно разложить на простые множители.
Слайд 8
ЗАДАНИЕ 2. Разложите на простые множители числа:
Используя эти разложения:
найдите НОК и
НОД этих чисел;
Извлеките квадратный корень из каждого числа.
Извлеките квадратный корень из каждого числа.
Слайд 10Целые числа (Z)
Отрицательные числа, противоположные натуральным
Число ноль
Натуральные числа
На множестве целых чисел
определены три арифметические операции –
сложение, вычитание, умножение.
сложение, вычитание, умножение.
Числа 2 и -2 называются противоположными.
Слайд 11ЗАДАНИЕ 3. Как изменится число, если в конце добавить ноль? Как изменится
число, если его умножить на ноль?
Как изменится число, если к нему прибавить ноль?
Слайд 16Рациональные числа (Q)–
это числа, которые можно представить в виде несократимой дроби.
Обыкновенные
Десятичные
Дроби
0,25
-3,04
1,75
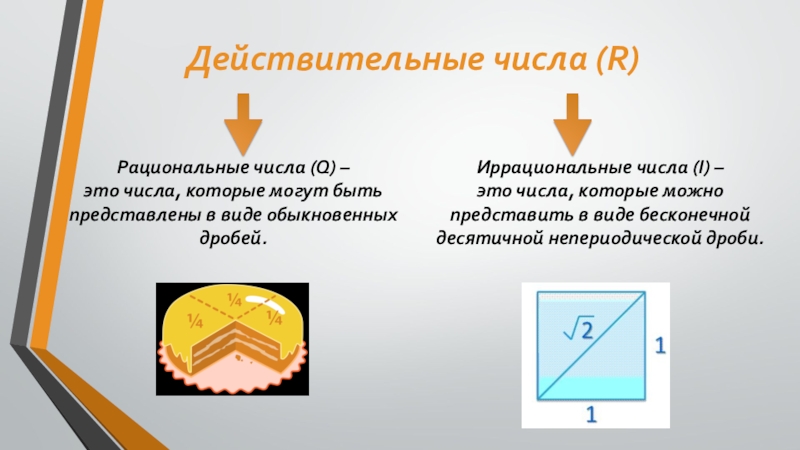
Слайд 20Действительные числа (R)
Рациональные числа (Q) –
это числа, которые могут быть представлены
в виде обыкновенных дробей.
Иррациональные числа (I) –
это числа, которые можно представить в виде бесконечной десятичной непериодической дроби.
Слайд 23Экспонента – число Эйлера или число Неппера.
Число е является базовым
соотношением роста для всех непрерывно растущих процессов.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других.
Самые известные иррациональные числа
Слайд 26Приближенные вычисления
ПРИМЕНЕНИЕ
Запись результатов измерений
Рациональные и иррациональные числа
Арифметические операции с различными числами
Слайд 27Приближенные вычисления применяются для записи результатов измерений
Масса Земли
Масса взрослого человека
Масса новорожденного
ребенка
Масса муравья
Масса муравья
83 кг
59721900000000000000000000 кг
0,000002 кг
3,65 кг
УСТАНОВИТЬ СООТВЕТСВИЕ
Слайд 28Приближенные вычисления применяются для сравнения рациональных и иррациональных чисел
Что их объединяет?
Чем
они отличаются?
Назовите натуральные числа, рациональные числа, действительные числа.
Расположите числа на числовой прямой.
Назовите натуральные числа, рациональные числа, действительные числа.
Расположите числа на числовой прямой.
Слайд 30Округлить число – значит сохранить в нем одну или несколько цифр,
считая слева направо, а остальные отбросить.
Чтобы округлить число до h значащих цифр, отбрасывают все цифры, стоящие справа от -ой значащей цифры, или если это нужно для сохранения разрядов, заменяют их нулями.
При этом, если первая из отброшенных цифр больше или равна 5, то последнюю оставшуюся цифру увеличивают на единицу. Если же отбрасывается только одна цифра 5, то последнюю из сохраняемых цифр оставляют без изменения, если она четная, и увеличивают на единицу, если она нечетная.
Правило округления:
Слайд 31Абсолютная погрешность – это модуль разности между точным и приближенным значением.
Найти абсолютную погрешность приближенных значений:
Слайд 32Абсолютная погрешность – это модуль разности между точным и приближенным значением.
Найти
абсолютную погрешность приближенных значений:
Слайд 33Относительная погрешность – это отношение абсолютной погрешности к модулю приближенного значения.
Найти относительную погрешность приближенных значений, выразить ее в процентах:
Слайд 34Относительная погрешность – это отношение абсолютной погрешности к модулю приближенного значения.
Найти относительную погрешность приближенных значений, выразить ее в процентах:
Слайд 35Арифметические операции с приближенными значениями:
Правило 1.
При сложении приближенные числа округляют
так, чтобы в них оставалось на один десятичный знак больше, чем в наиболее грубом слагаемом. Полученную сумму округляют до количества десятичных знаков наиболее грубого слагаемого.
Пример. Найти сумму чисел 1,2; -2,35; 3,454; 4,5543.
1,2 – 2,35 + 3,45 + 4,55= 6,85= 6,8.
Пример. Найти сумму чисел 1,2; -2,35; 3,454; 4,5543.
1,2 – 2,35 + 3,45 + 4,55= 6,85= 6,8.
Слайд 36Арифметические операции с приближенными значениями:
Правило 2.
При вычитании не следует производить
округление приближенных чисел, так как может произойти потеря точности окончательного результата (особенно в случае, когда уменьшаемое и вычитаемое – числа, близкие по абсолютной величине).
Пример. 47,104 - 47,1=0,004.
Если уменьшаемое округлить, отбросив последний десятичный знак, то в результате разность будет равна нулю (47,10 - 47,1 = 0), что может внести ошибку в окончательный результат вычислений.
Пример. 47,104 - 47,1=0,004.
Если уменьшаемое округлить, отбросив последний десятичный знак, то в результате разность будет равна нулю (47,10 - 47,1 = 0), что может внести ошибку в окончательный результат вычислений.
Слайд 37Арифметические операции с приближенными значениями:
Правило 3.
При умножении и делении приближенные
числа округляют так, чтобы в них оставалось на одну значащую цифру больше, чем их имеется в числе с наименьшим количеством значащих цифр. Полученный результат округляют до числа, имеющего столько значащих цифр, сколько их имелось в числе с наименьшим количеством значащих цифр.
Примеры:
Найти произведение 2. Найти частное от деления
12,2×73,564. 25,713 : 3,6.
12,2×73,56 = 897,432 = 897,4. 25,71 : 3,6 = 7,1416 = 7,1.
Примеры:
Найти произведение 2. Найти частное от деления
12,2×73,564. 25,713 : 3,6.
12,2×73,56 = 897,432 = 897,4. 25,71 : 3,6 = 7,1416 = 7,1.
Слайд 38Арифметические операции с приближенными значениями:
Правило 4.
При возведении приближенного числа в
степень в окончательном результате сохраняют столько значащих цифр, сколько имелось их в самом приближенном числе.
Пример. 9,862 = 97,2196 = 97,21.
Пример. 9,862 = 97,2196 = 97,21.
