- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме биквадратные уравнения
Содержание
- 1. Презентация по теме биквадратные уравнения
- 2. Литература : С.М. Никольский и др.
- 3. Уравнение вида
- 4. № 356. Представьте выражение в виде квадрата: a)
- 5. Пример 1Решить уравнение Решениевведем новую переменную
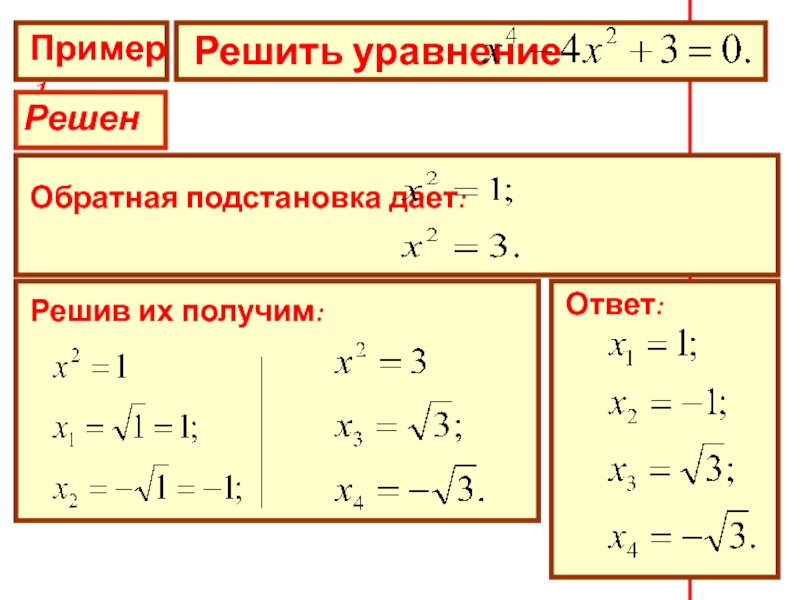
- 6. Пример 1Решить уравнение РешениеОбратная подстановка дает: Решив их получим:Ответ:
- 7. Пример 2Решить уравнение Решениевведем новую переменную
- 8. Пример 2Решить уравнение Решениевведем новую переменную
- 9. Пример 3Решить уравнение Решениевведем новую переменную
- 10. Пример 4Решить уравнение Решениевведем новую переменную
- 11. Пример 5Решить уравнение Решениевведем новую переменную
- 12. Замечание 1Решить уравнениеИмеет один кореньОтвет: Решить уравнениеРешение:Ответ: -1; 0; 1.
- 13. Замечание 2 Из рассмотренных примеров видно, что биквадратное
- 14. Решить номера №№358, 359, 360.
Слайд 2
Литература : С.М. Никольский и др.
Слайд 3
Уравнение вида
а, b, c – данные числа и а отлично от нуля, а х –неизвестное, называют биквадратным уравнением.
Чтобы решить биквадратное уравнение, вводят новое неизвестное при помощи равенства у = х2
Тогда исходное уравнение превращается в квадратное относительно неизвестного y.
Слайд 4№ 356. Представьте выражение в виде квадрата:
a) х4; б) а6; в) у8; г) m10.
№
а) х4 +2х2 + 1 = 0; б) m4 – 3 + 2m2 =0;
в) 4у2 – 7у4 = 0; г) 15 – х4 + 2х2 = 0;
д) х6 – 3х3 + 2 = 0; е) у8 – 4 = 0.
Слайд 5
Пример 1
Решить уравнение
Решение
введем новую переменную
исходное уравнение примет вид:
так как то оно имеет два корня.
По теореме обратной теореме Виета имеем:
Слайд 7
Пример 2
Решить уравнение
Решение
введем новую переменную
исходное уравнение примет вид:
так как то оно имеет два корня.
Определим корни по формуле
Слайд 8
Пример 2
Решить уравнение
Решение
введем новую переменную
исходное уравнение примет вид:
- исключается
Обратная подстановка дает:
Ответ:
Слайд 9
Пример 3
Решить уравнение
Решение
введем новую переменную
исходное уравнение примет вид:
Его дискриминант
следовательно оно не имеет корней. Тогда и исходное уравнение тоже не имеет корней.
Ответ: корней нет.
Слайд 10
Пример 4
Решить уравнение
Решение
введем новую переменную
исходное уравнение примет вид:
Его дискриминант
следовательно оно имеет единственный корень.
Обратная подстановка дает:
Ответ:
Слайд 11
Пример 5
Решить уравнение
Решение
введем новую переменную
исходное уравнение примет вид:
для которого
таким образом оно имеет единственный корень
Значит исходное уравнение не имеет корней.
Ответ: корней нет.
Слайд 13
Замечание 2
Из рассмотренных примеров видно, что биквадратное уравнение может иметь четыре,
Скоро мы познакомимся с комплексными числами и узнаем, что биквадратное уравнение имеет, вообще говоря, четыре комплексных корня.
Впрочем, бывает, что их меньше чем четыре, но в таких случаях считают, что некоторые корни кратные.