- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике(алгебре) на тему Способы решения показательных уравнений
Содержание
- 1. Презентация по математике(алгебре) на тему Способы решения показательных уравнений
- 2. Тема :Способы решения показательных уравнений
- 3. «Уравнения- это золотой ключ, открывающий все математические
- 4. Задача:
- 5. Опрос:1.Какие уравнения называются показательными?2. Выберите показательные уравнения:
- 6. 3.Закончите выражения:an *am =an /am =(an )m =an *bn =a0 =a-n =
- 7. Закончите выражения:38 *35 =25 /23 =23 *33 =3-3 =3-2 =70=
- 8. Слайд 8
- 9. Историю представим мы немного, события расставив по
- 10. О том еще известна нам легенда, что
- 11. Все знают, что такое ростовщик. Тот человек
- 12. Пятнадцатый век – рожденье банков, дающих деньги
- 13. Его развили математик Штифель, Оресм, Шюке, затем
- 14. 4. Какие способы решения показательных
- 15. «Теория без практики мертва и бесплодна, практика
- 16. Решение заданий:Решить уравнения: x .
- 17. Слайд 17
- 18. Алгоритм решения показательных уравненийОпределить вид уравненияПодобрать соответствующий способ решения среди изученныхРешить по соответствующему способуЗаписать ответ
- 19. И её применение в природе и технике.ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
- 20. Подумайте! Где может использоваться показательная функция?Тема «Показательная
- 21. Наглядный бытовой пример!Все, наверное, замечали, что если
- 22. При падении тел в безвоздушном пространстве скорость
- 23. Когда радиоактивное вещество распадется, его количество уменьшается.
- 24. Давление атмосферы, выраженное в миллиметрах ртутного столба,
- 25. Как видите, во всех
- 26. Самостоятельная работа«Математику нельзя изучать, наблюдая, как это
- 27. Оценка самостоятельных письменных работ:Оценка "5" ставится, если
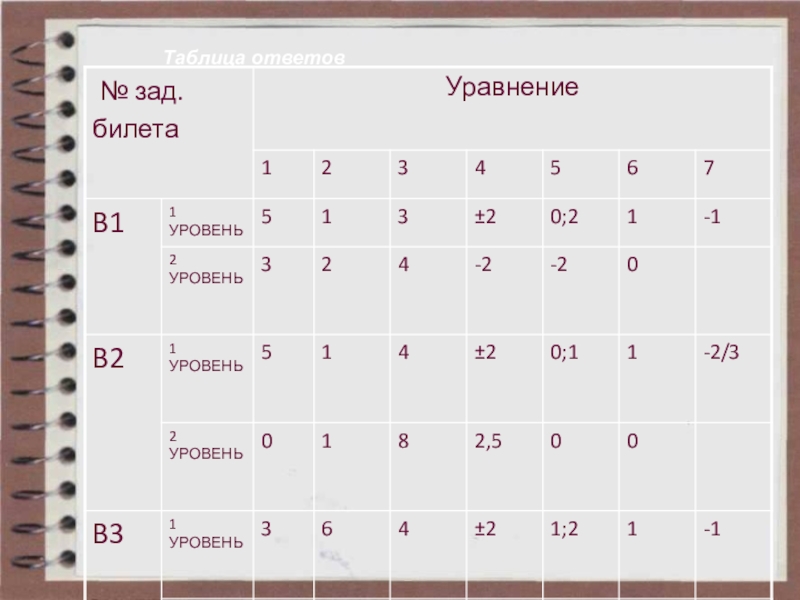
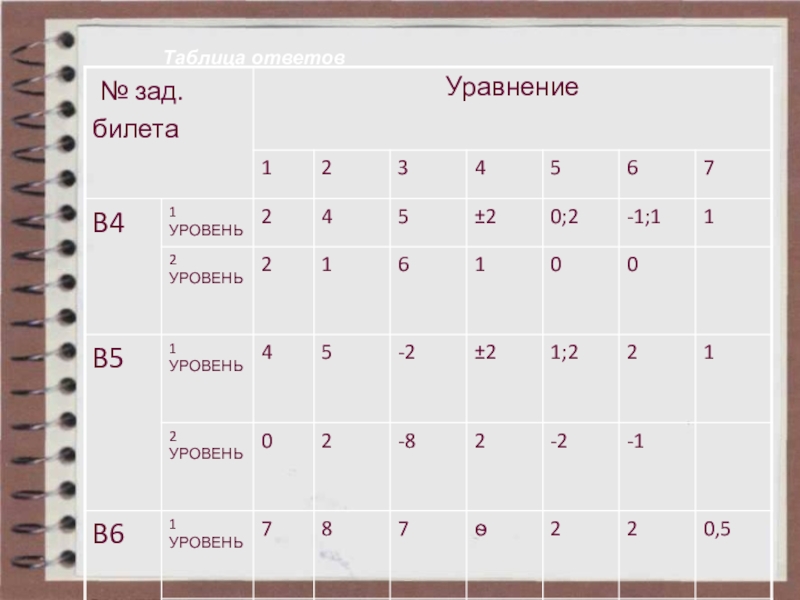
- 28. Таблица ответов
- 29. Таблица ответов
- 30. Достигнуты ли цели урока?Какими методами можно решать показательные уравнения?Оценка знаний учащихсяИтог урока:
- 31. Задание на дом: 1.конспект;2.
- 32. Спасибо за урок ! Решать, работать можно
- 33. Показательная функция в природе и технике
- 34. «Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде всего показательные, открывают доступ ко многим исследованиям»Л. Эйлер
- 35. При искусственном выращивании каких-либо микроорганизмов размножение клеток
- 36. При передаче электроэнергии по подводному кабелю потери
- 37. Если однолетнее растение дает 100 семян и
- 38. В XIV-XV веках в Западной Европе появляются
- 39. По закону показательной функции размножалось бы все
- 40. Если бы все маковые зерна давали всходы,
- 41. Потомство комнатных мух за лето только от
- 42. В природе, технике и экономике встречаются многочисленные
- 43. Радиоактивный распад вещества – процессу органического затухания
- 44. В биологии процесс выравнивания встречается при разрушении
Слайд 1Методическая разработка
урока математики
Тема :Способы решения показательных уравнений
Хорошайло Галина Васильевна - преподаватель
Государственное бюджетное образовательное учреждение среднего профессионального образования(ССУЗ)
Каслинского промышленно-гуманитарного техникума
Слайд 9
Историю представим мы немного, события расставив по порядку: вы знаете, еще
Слайд 10
О том еще известна нам легенда, что как-то у арабского царя
Слайд 11Все знают, что такое ростовщик. Тот человек проценты брать привык. Они встречались
Слайд 12
Пятнадцатый век – рожденье банков, дающих деньги людям под процент, тогда
Слайд 13Его развили математик Штифель, Оресм, Шюке, затем Исаак Ньютон. И в
Слайд 14 4. Какие способы решения показательных уравнений вы знаете?
Это:
1).Приравнивание
2). Вынесение общего множителя за скобки
3). Введение новой переменной
4). Способ группировки;
5). Сведение уравнения к квадратному;
6). Графический
7). Метод почленного деления
Слайд 15«Теория без практики мертва и бесплодна, практика без теории невозможна
М.В.Ломоносов
Слайд 18Алгоритм решения показательных уравнений
Определить вид уравнения
Подобрать соответствующий способ решения среди изученных
Решить
Записать ответ
Слайд 20Подумайте! Где может использоваться показательная функция?
Тема «Показательная функция» является основополагающей при
Слайд 21Наглядный бытовой пример!
Все, наверное, замечали, что если снять кипящий чайник с
T=(T1-T0)e-kt+T1,
где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.
Слайд 22При падении тел в безвоздушном пространстве скорость их непрерывно возрастает.
При падении
v=mg/k(1-e)-kt/m
Слайд 23Когда радиоактивное вещество распадется, его количество уменьшается. Через некоторое время остается
m = m0(1/2)-t/t0
Явление радиоактивного распада используется для определения возраста археологических находок, например, определен примерный возраст Земли, около 5,5 млрд. лет, для поддержания эталона времени.
Слайд 24Давление атмосферы, выраженное в миллиметрах ртутного столба, меняется по закону: Р
Показательная функция также используется при решении некоторых задач судовождения
Слайд 27Оценка самостоятельных письменных работ:
Оценка "5" ставится, если студент:
1. выполнил работу без
2. допустил не более одного недочета.
Оценка "4" ставится, если студент выполнил работу полностью, но допустил в ней
не более одной негрубой ошибки и одного недочета;
или не более двух недочетов.
Оценка "3" ставится, если студент правильно выполнил не менее половины работы
не более двух грубых ошибок;
или не более о; той грубой и одной негрубой ошибки и одного недочета;
или не более двух-трех негрубых ошибок;
или одной негрубой ошибки и трех недочетов;
или при отсутствии ошибок, но при наличии четырех-пяти недочетов.
Оценка "2" ставится, если студент:
допустил число ошибок и недочетов превосходящее норму, при которой может быть выставлена оценка "3";
или если правильно выполнил менее половины работы.
Слайд 30Достигнуты ли цели урока?
Какими методами можно решать показательные уравнения?
Оценка знаний учащихся
Итог
Слайд 31Задание на дом: 1.конспект;
2. прорешать уравнения из списка
Сильным: 2,3,4, 6, 8
Остальным:2,4,6 ( можно на выбор)
Слайд 32Спасибо за урок !
Решать, работать можно вечно.
Вселенная ведь бесконечна.
Спасибо всем
А главное, чтоб был он впрок!
Мне очень понравилось с вами работать
Слайд 34«Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде всего показательные, открывают
Л. Эйлер
Слайд 35При искусственном выращивании каких-либо микроорганизмов размножение клеток идет так, что за
Поэтому, когда время увеличивается на длину митотического цикла, число клеток увеличивается в два раза
Органический рост
Слайд 36При передаче электроэнергии по подводному кабелю потери в силе тока за
Например, на каждом километре сила тока уменьшается на 0,5%. Тогда при увеличении расстояния от источника энергии на 1 км сила тока будет изменяться в отношении 1: 0,995
Потери силы тока.
Слайд 37Если однолетнее растение дает 100 семян и из них прорастает половина,
Органический рост
Слайд 38
В XIV-XV веках в Западной Европе появляются банки – учреждения, которые
Эта сумма выражается формулой
Пример. Банк выплачивает вкладчикам проценты по вкладам в размере 4% в год, т.е. за каждый год вклад увеличивается в 1,04 раза.
Рост вклада в банке
Слайд 39По закону показательной функции размножалось бы все живое на Земле, если
Слайд 40Если бы все маковые зерна давали всходы, то через 5 лет
Слайд 41Потомство комнатных мух за лето только от одной самки может составить
Слайд 42В природе, технике и экономике встречаются многочисленные процессы, в ходе которых
Слайд 43Радиоактивный распад вещества – процессу органического затухания Явление радиоактивного распада используется
Законам органического роста подчиняется рост вклада в банке
восстановление гемоглобина в крови донора или раненого, потерявшего много крови
рост дрожжей, ферментов, микроорганизмов.
Закон органического роста выражается формулой: N=N0 ext .
По этому же закону изменяется количество древесины в дереве, что имеет большое значение для рационального ведения лесного хозяйства.
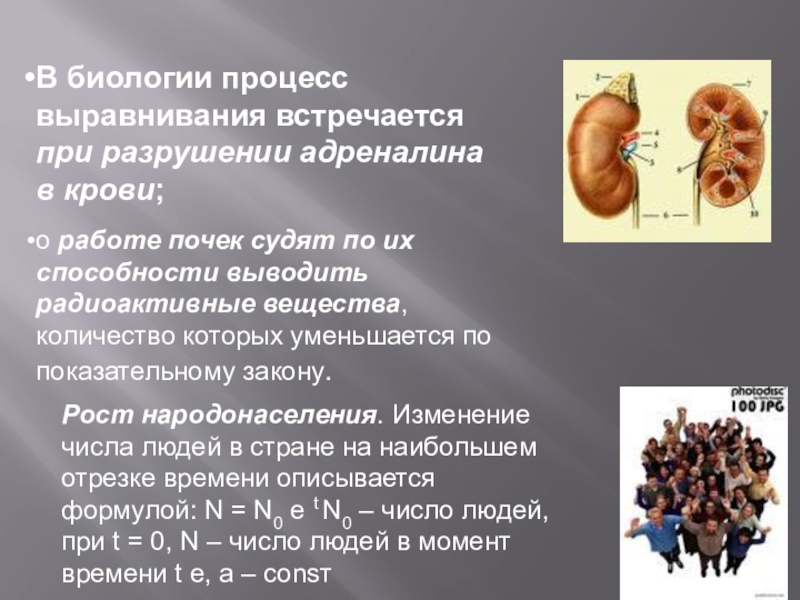
Слайд 44В биологии процесс выравнивания встречается при разрушении адреналина в крови;
о
Рост народонаселения. Изменение числа людей в стране на наибольшем отрезке времени описывается формулой: N = N0 e t N0 – число людей, при t = 0, N – число людей в момент времени t e, a – consт