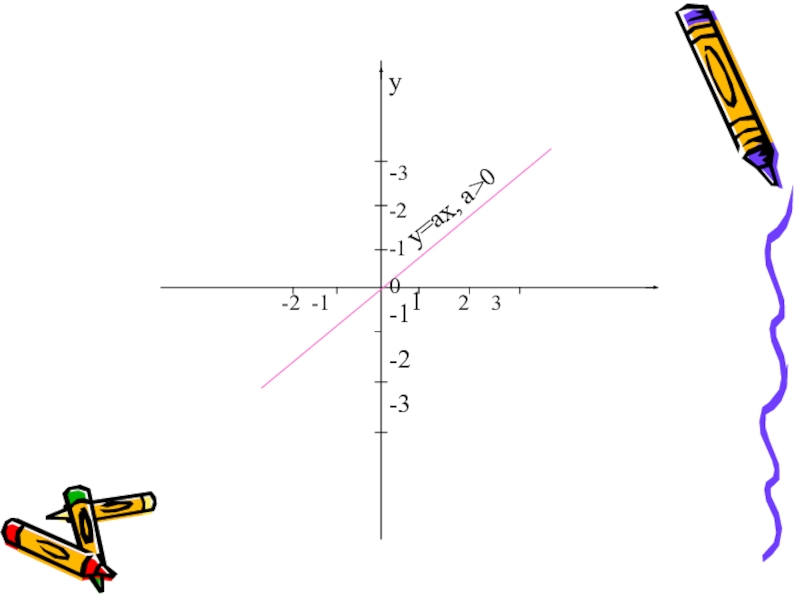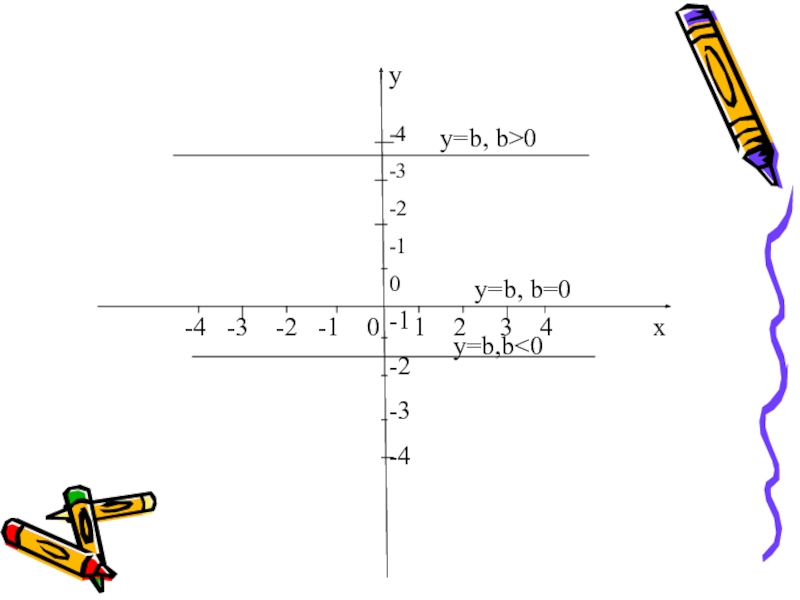- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике В мире функций (9 класс)
Содержание
- 1. Презентация по математике В мире функций (9 класс)
- 2. Цели и задачиИзучить свойства и графики квадратичной
- 3. Содержание учебного проектаОпределение функции;Виды функций и их
- 4. Определение функцииФункция — одно из важнейших математических
- 5. Что такое функцияПеременную х называют независимой переменной
- 6. Способ записи функцииЕсли зависимость переменной у от
- 7. Область определения функцииВсе значения независимой переменной образуют
- 8. Возрастающая функция – если для любых x1и x2, таких, что x1
- 9. Функция является нечетной – если для любого
- 10. Линейная функция- функция, которая задана формулой y=kx+b,
- 11. y3210-1-2-3 -3 -2 -1
- 12. Прямая пропорциональность- функция, заданная формулой y=ax, где
- 13. y-3-2-10-1-2-3-2 -1 1 2 3 y=ax, a>0
- 14. Постоянная функция- функция, заданная формулой y=b, где
- 15. y-4-3-2-10 -4
- 16. Обратная пропорциональность- функция, заданная формулой y=k/x, где число k-коэффициент обратной пропорциональности.Свойства функции y=k/xГрафикОбратная пропорциональность
- 17. 1.Область определения- множество всех действительных чисел, кроме
- 18. y=6/xy54321-1-2-3-4-5-6-4 -3 -2 -1 0
- 19. Квадратичная функцияКвадратичной функцией называется функция, которую можно
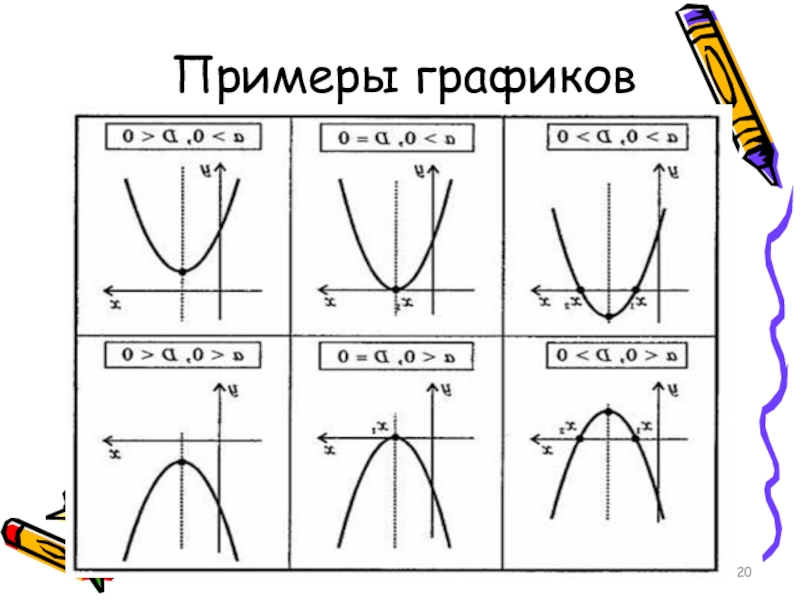
- 20. Примеры графиков
- 21. Что является графиком квадратичной функции.Графиком квадратичной функции
- 22. *Построение графика функции1) найти координаты вершины параболы
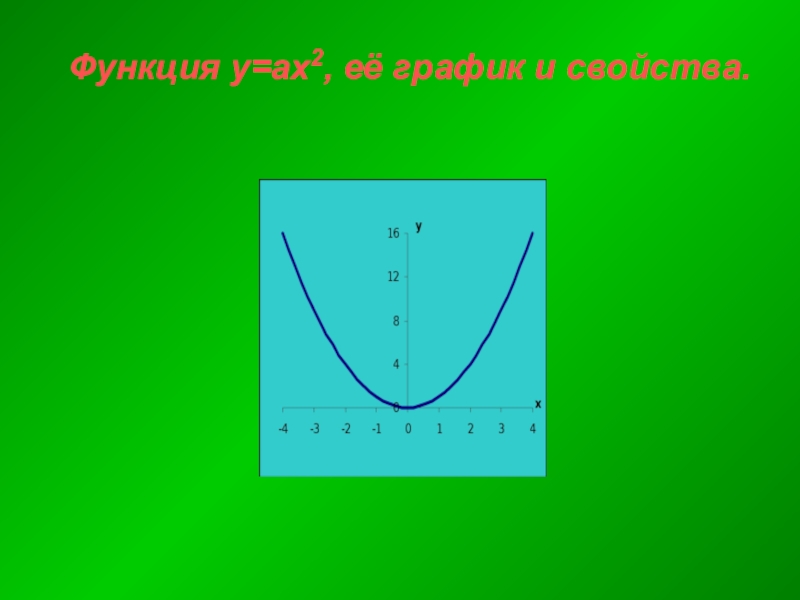
- 23. Функция y=ах2, её график и свойства.
- 24. У=ах².а=1 функция принимает вид у=х². Её
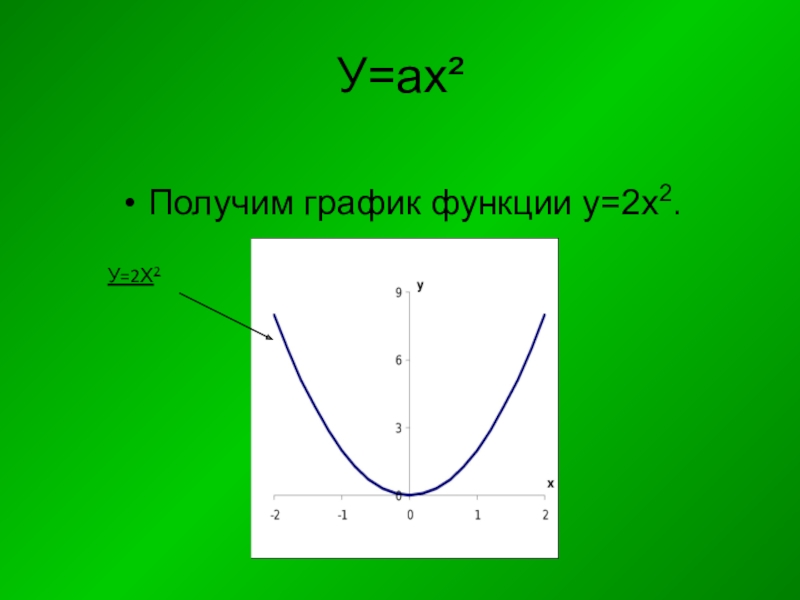
- 25. У=ах²Получим график функции у=2х2.У=2Х2
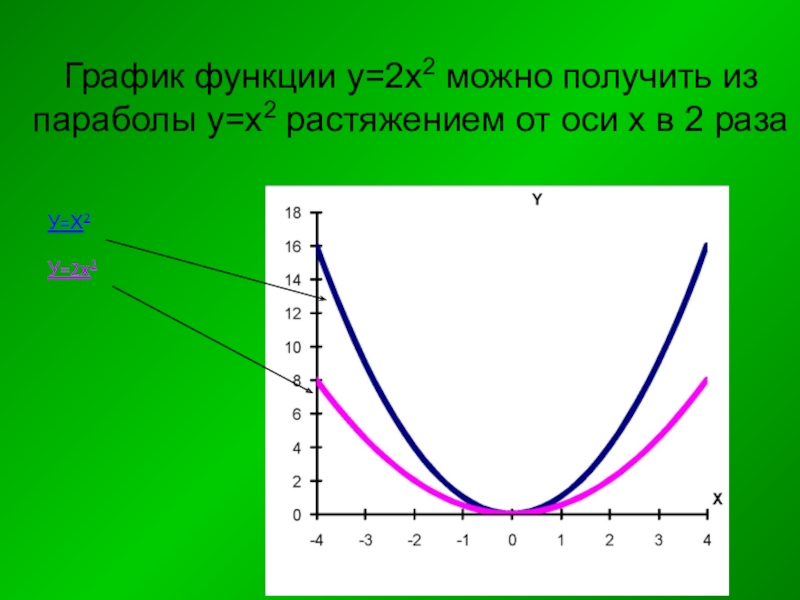
- 26. График функции у=2х2 можно получить из параболы у=х2 растяжением от оси х в 2 разаУ=Х2У=2х2
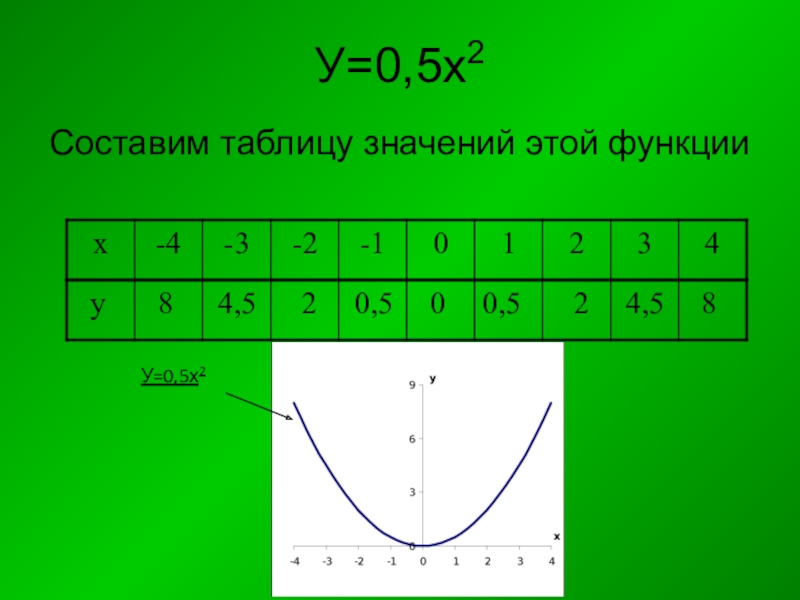
- 27. У=0,5х2Составим таблицу значений этой функцииУ=0,5х2
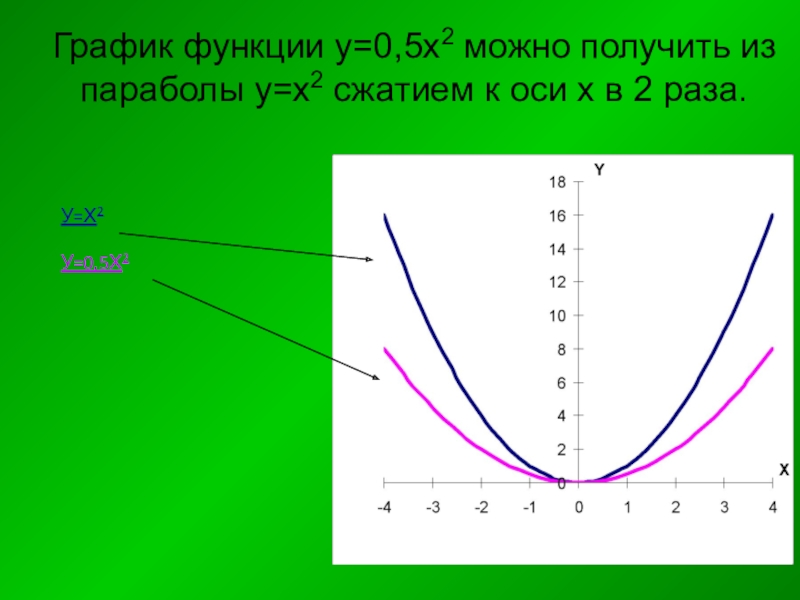
- 28. График функции у=0,5х2 можно получить из параболы у=х2 сжатием к оси х в 2 раза.У=Х2У=0,5Х2
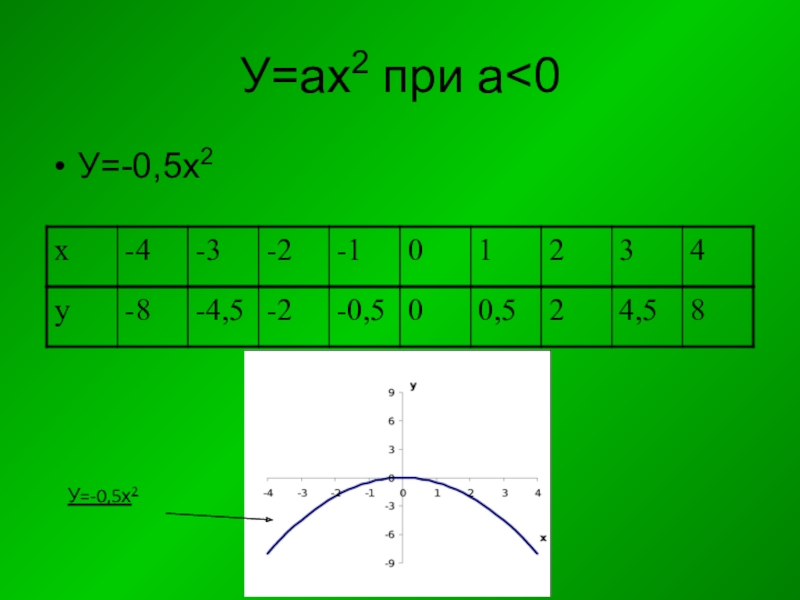
- 29. У=ах2 при а
- 30. График функции у=-0,5х2 может быть получен из
- 31. Свойства функции у=ах2Если а>0:1. Если х=0, то
- 32. Без квадратичной функции нельзя понять закономерности в живой природе
- 33. Пример №1.Если мы измерим длину и ширину
- 34. Пример №2. Возьмём генетически-однородный чисто-сортный материал –
- 35. Распределение вариантов в вариационном ряду можно выразить
- 36. Вывод: Развитие жизни на земле описывается математическими
- 37. Итог исследовательской работыИзучили, систематизировали и обобщили знания
- 38. В мире функцийРаботу подготовилаГоголева МарияГКОУ «Созвездие»
Цели и задачиИзучить свойства и графики квадратичной функцииНаучиться выполнять построения по данным условиямПоказать применение квадратичной функции в природе
Слайд 2Цели и задачи
Изучить свойства и графики квадратичной функции
Научиться выполнять построения по
данным условиям
Показать применение квадратичной функции в природе
Показать применение квадратичной функции в природе
Слайд 3Содержание учебного проекта
Определение функции;
Виды функций и их графики:
линейная функция;
обратная пропорциональность;
квадратичная функция;
Построение графиков;
Применение квадратичной функции.
квадратичная функция;
Построение графиков;
Применение квадратичной функции.
Слайд 4Определение функции
Функция — одно из важнейших математических понятий.
Функцией называют такую
зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Слайд 5Что такое функция
Переменную х называют независимой переменной или аргументом. Переменную у
называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Слайд 6Способ записи функции
Если зависимость переменной у от переменной х является функцией,
то коротко это записывают так: y=f(x). (Читают: у равно f от х.) Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х.
Слайд 7Область определения функции
Все значения независимой переменной образуют область определения функции.
Если
функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Слайд 8Возрастающая функция – если для любых x1и x2, таких, что x1
выполняется неравенство
f(x1)Убывающая функция – если для любых x1 и x2, таких, что x1 выполняется неравенство f(x1)>f(x2)
f(x1)
Монотонность функции
Слайд 9Функция является нечетной – если для любого x из области определения
функции выполняется равенство
f(-x)=-f(x)
Четная функция
Функция является четной – если для любого x из области определения функции выполняется равенство
f(-x)=f(x)
f(-x)=-f(x)
Четная функция
Функция является четной – если для любого x из области определения функции выполняется равенство
f(-x)=f(x)
Нечетная функция
Слайд 10
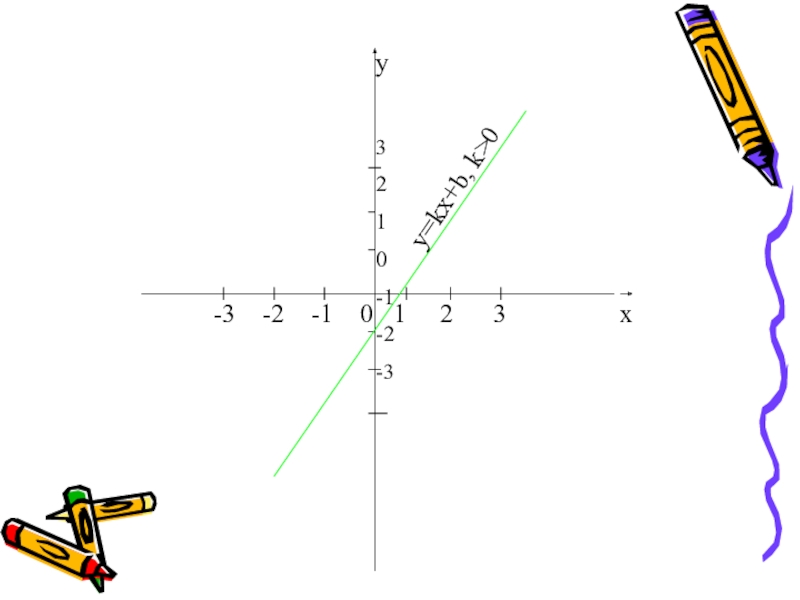
Линейная функция- функция, которая задана формулой y=kx+b, где k и b-
действительные числа.
Графиком линейной функции является прямая.
Если к>0,функция возрастает на всей числовой прямой, если к<0, функция убывает.
Графиком линейной функции является прямая.
Если к>0,функция возрастает на всей числовой прямой, если к<0, функция убывает.
Линейная функция
Слайд 12
Прямая пропорциональность- функция, заданная формулой y=ax, где число a- коэффициент пропорциональности.
Свойства
функции y=ax:
1.Область определения функции- множество всех действительных чисел
2.y=ax- нечетная функция
3.При a>0 функция возрастает, а при a<0 убывает на всей числовой прямой
1.Область определения функции- множество всех действительных чисел
2.y=ax- нечетная функция
3.При a>0 функция возрастает, а при a<0 убывает на всей числовой прямой
Прямая пропорциональность
Слайд 14
Постоянная функция- функция, заданная формулой y=b, где b-некоторое число.
Графиком постоянной
функции y=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат
Постоянная функция
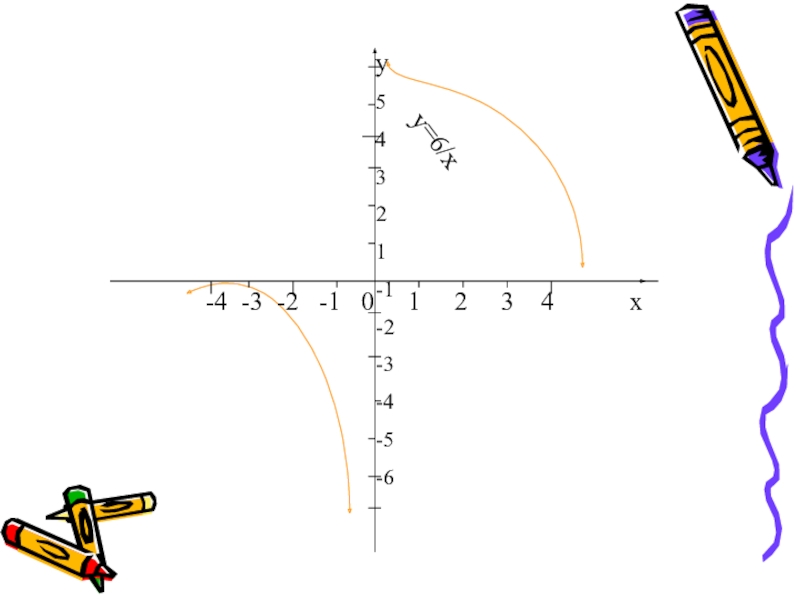
Слайд 16Обратная пропорциональность- функция, заданная формулой y=k/x, где число k-коэффициент обратной пропорциональности.
Свойства
функции y=k/x
График
График
Обратная пропорциональность
Слайд 171.Область определения- множество всех действительных чисел, кроме нуля
2.y=k/x- нечетная функция
3.Если k>0,
то функция убывает на промежутке (0;+Г) и на промежутке (-Г;+0). Если k<0, то функция возрастает на промежутке (-Г;0) и на промежутке (0;+Г)
Графиком является гипербола
Графиком является гипербола
Свойства функции обратной пропорциональности
Слайд 19Квадратичная функция
Квадратичной функцией называется функция, которую можно записать формулой вида
y = ax2 + bx + c, где x – независимая переменная, a, b и c – некоторые числа, причем a≠0.
Свойства функции и вид ее графика определяются, в основном, значениями коэффициента a и дискриминанта:
Свойства функции и вид ее графика определяются, в основном, значениями коэффициента a и дискриминанта:
Слайд 21
Что является графиком квадратичной функции.
Графиком квадратичной функции является парабола – кривая,
симметричная относительно прямой , проходящей через вершину параболы (вершиной параболы называется точка пересечения параболы с осью симметрии).
Чтобы построить график квадратичной функции, нужно:
Чтобы построить график квадратичной функции, нужно:
Слайд 22*
Построение графика функции
1) найти координаты вершины параболы и отметить ее в
координатной плоскости;
2) построить еще несколько точек, принадлежащих параболе;
3) соединить отмеченные точки плавной линией.
2) построить еще несколько точек, принадлежащих параболе;
3) соединить отмеченные точки плавной линией.
Слайд 24У=ах².
а=1 функция принимает вид у=х².
Её графиком является парабола.
а=2.
Построим график функции у=2х². Составим таблицу значений этой функции:
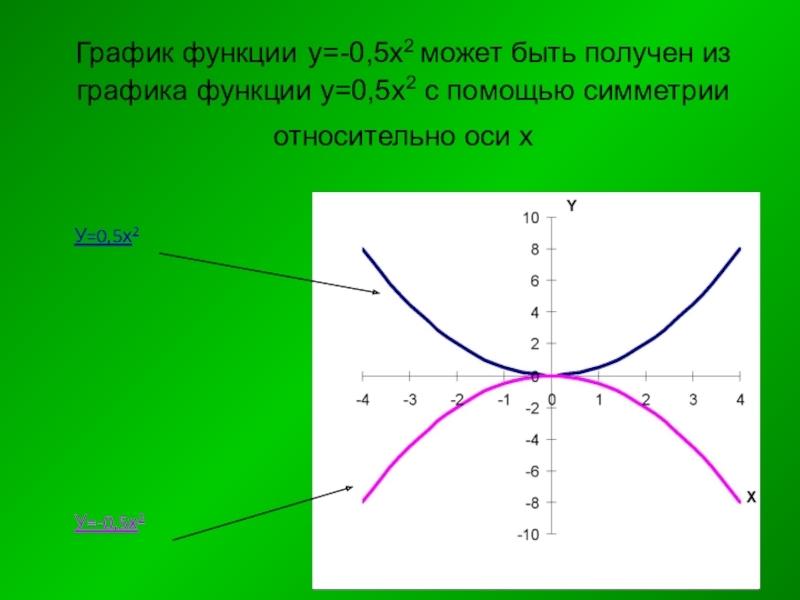
Слайд 30График функции у=-0,5х2 может быть получен из графика функции у=0,5х2 с
помощью симметрии относительно оси х
У=0,5х2
У=-0,5х2
Слайд 31Свойства функции у=ах2
Если а>0:
1. Если х=0, то у=0. График функции проходит
через начало координат.
2. Если х – не = 0, то у>0. График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси х.
4. Функция убывает в промежутке
(-∞;0] и возрастает в промежутке [0;+∞).
5. Наименьшее значение, равно 0, функция принимает при х=0, наибольшего значения функция не имеет. Областью значений функции является промежуток [0;+∞)
2. Если х – не = 0, то у>0. График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси х.
4. Функция убывает в промежутке
(-∞;0] и возрастает в промежутке [0;+∞).
5. Наименьшее значение, равно 0, функция принимает при х=0, наибольшего значения функция не имеет. Областью значений функции является промежуток [0;+∞)
Если а<0:
1. Если х=0, то у=0. График функции проходит через начало координат.
2. Если х не =0, то у=0. График функции расположен в нижней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
4. Функция возрастает в промежутке (-∞;0] и убывает в промежутке [0;+∞)
5. Наибольшее значение, равное нулю, функция принимает при х=0, наименьшего значения функция не имеет. Область значений функции – промежуток (-∞;0].
Слайд 33Пример №1.
Если мы измерим длину и ширину листьев, взятых с одного
дерева, то увидим, что размеры их варьируют в довольно широких пределах. Расположим некоторое количество листьев в порядке нарастания или убывания их длины. Получим ряд изменчивости длины (вариационный ряд), слагающийся из отдельных вариант. Если мы подсчитаем число отдельных вариант, то заметим, что чаще всего встречаются средние члены ряда, а к обоим концам ряда частота встречаемости будет снижаться.
Слайд 34Пример №2. Возьмём генетически-однородный чисто-сортный материал – колос пшеницы, и изучим изменчивость
числа колосков в колосе. Замечаем, что число колосков в разных колосьях варьирует от 14 до 20. Чаще всего встречаются колосья со средним числом колосков (16-18), реже с большим или меньшим числом их.
Вот результат подсчёта (ряд – 100 колосьев): Число колосков в колосе – 14 15 16 17 18 19 20
Количество колосьев – 2 7 22 32 24 8 3
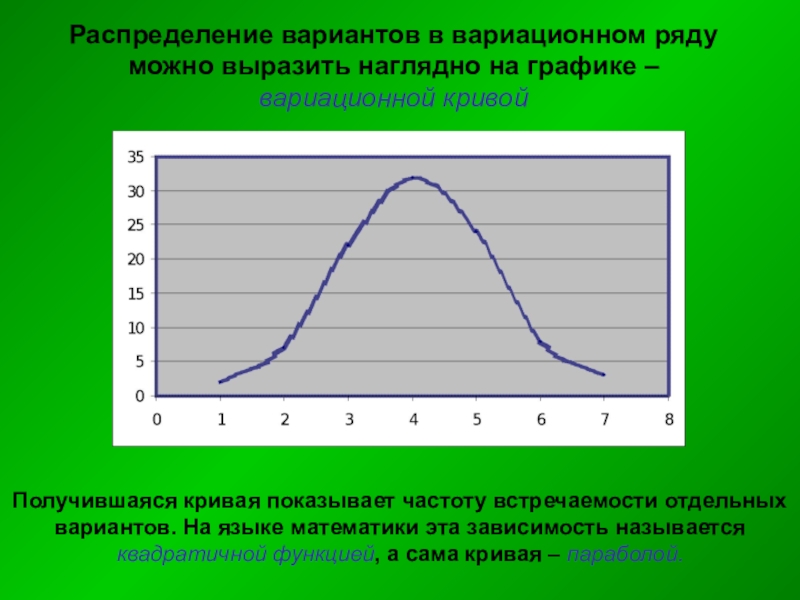
Слайд 35Распределение вариантов в вариационном ряду можно выразить наглядно на графике –
вариационной кривой
Получившаяся кривая показывает частоту встречаемости отдельных вариантов. На языке математики эта зависимость называется квадратичной функцией, а сама кривая – параболой.
Слайд 36Вывод: Развитие жизни на земле описывается математическими законами – ФУНКЦИЯМИ. Изучив квадратичную
функцию, мы сможем успешно овладеть другими науками.
Слайд 37Итог исследовательской работы
Изучили, систематизировали и обобщили знания по теме «Квадратичная функция»
Научились
строить графики различных функций
Научились представлять информацию в графическом редакторе Microsoft Power Point
Научились представлять информацию в графическом редакторе Microsoft Power Point
