- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике в 9 кл Арифметическая прогрессия
Содержание
- 1. Презентация по математике в 9 кл Арифметическая прогрессия
- 2. Устный счет1) Последовательность уn задана
- 3. 4; 6; 8; 10; …
- 4. Что такое прогрессия? Это частный случай
- 5. Определение арифметической прогрессии Числовую
- 6. Разность арифметической прогрессии
- 7. Дано: (аn) – арифметическая прогрессия, a1- первый
- 8. Характеристическое свойство: Любой член арифметической
- 9. Способы задания арифметической прогрессииа) рекуррентной формулой:
- 10. № 621 Дано: ( an ): 2;
- 11. № 627 (а,г) Дано: ( an )
- 12. № 622Дано: а1=3; d = 2; an=
- 13. № 630(а)В арифметической прогрессии (an ) найти
- 14. № 632 (а)Является ли число 12 членом
- 15. Дополнительное заданиеВ арифметической прогрессии найти a10, если
- 16. Самостоятельная работа Дидактические материалы
- 17. Итог урокаКакую последовательность называют арифметической прогрессией? Что
- 18. Домашнее задание §6, п.6.1., № 629, 633.СПАСИБО ЗА УРОК
Устный счет1) Последовательность уn задана формулой уn= 9 – 5n. Найдите у2,
Слайд 2Устный счет
1) Последовательность уn задана формулой
уn= 9 – 5n.
Найдите у2, у3, у5.
2) Последовательность задана формулой
an = 15 – 3n.
Найдите номер члена последовательности, равного 6; 0; -3; -9.
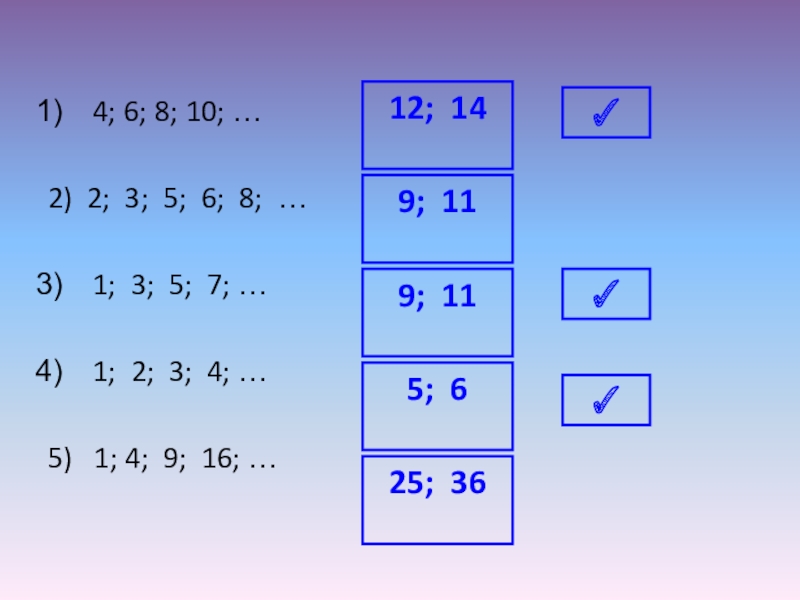
Слайд 34; 6; 8; 10; …
2) 2; 3; 5; 6; 8; …
1; 3; 5; 7; …
1; 2; 3; 4; …
5) 1; 4; 9; 16; …
12; 14
9; 11
9; 11
5; 6
25; 36
✓
✓
✓
Слайд 4Что такое прогрессия?
Это частный случай числовой последовательности.
Слово прогрессия латинского происхождения и означает «движение вперед».
Прогрессии были известны в Древнем Египте и Вавилоне около 2000 лет до н.э.
Прогрессии были известны в Древнем Египте и Вавилоне около 2000 лет до н.э.
Слайд 5Определение арифметической прогрессии
Числовую последовательность,
каждый последующий
член которой равен предшествующему, сложенному с постоянным для данной последовательности числом, называют арифметической прогрессией.
Слайд 7Дано: (аn) – арифметическая прогрессия, a1- первый член прогрессии, d –
разность.
a2 = a1 + d
a3 = a2 + d =(a1 + d) + d = a1+2d
a4 = a3 + d =(a1+2d) +d = a1+3d
a5 = a4 + d =(a1+3d) +d = a1+4d
. . .
a2 = a1 + d
a3 = a2 + d =(a1 + d) + d = a1+2d
a4 = a3 + d =(a1+2d) +d = a1+3d
a5 = a4 + d =(a1+3d) +d = a1+4d
. . .
Задание арифметической прогрессии формулой n – ого члена
an = a1+ (n-1)·d
Слайд 8Характеристическое свойство:
Любой член арифметической прогрессии, кроме первого, есть среднее
арифметическое предшествующего и последующего членов.
Слайд 9Способы задания арифметической прогрессии
а) рекуррентной формулой:
б) формулой n-го члена:
в) формулой вида:
Слайд 10№ 621
Дано: ( an ): 2; 7; 12; 22; 27; …
Найти:
а) разность между последующим членом
и предыдущим;
б) ( an ) – арифметическая прогрессия?
Решение:
a2 – a1 = a3 – a2 = a5 – a4 =7 – 2 = 12 – 7= 27 – 22 =5,
но a4 – a3 =22 – 12 =10,
10≠5,
значит, …
и предыдущим;
б) ( an ) – арифметическая прогрессия?
Решение:
a2 – a1 = a3 – a2 = a5 – a4 =7 – 2 = 12 – 7= 27 – 22 =5,
но a4 – a3 =22 – 12 =10,
10≠5,
значит, …
аn не арифметическая прогрессия
Слайд 11
№ 627 (а,г)
Дано: ( an ) – арифметическая прогрессия
а)а3=5; a4=9.
Найти:
a2 и d.
Решение:
Решение:
г) а6= – 15; a8= –11 .
Найти: a7 и d.
Решение:
d =a4 – a3= 9 – 5 =4,
a2=a3 – d= 5 – 4 = 1.
Или a3 =(a2+a4):2, тогда
a2= 2a3–a4 =2·5 – 9 = 1
Ответ: a2=1, d=4.
a7 = (a6+a8): 2,
a7 =(–15 – 11):2= – 13,
d =a8 – a7= –11 –(–13)= 2.
Ответ: a7= –13, d=2.
Слайд 12№ 622
Дано: а1=3; d = 2; an= a1 +(n - 1)·d
. Найти пять первых членов арифметической прогрессии.
Решение:
а2 = a1 + d= 3+2=…
a3= a1 +2d=….
a4 =…
a5 =…
Ответ:
Решение:
а2 = a1 + d= 3+2=…
a3= a1 +2d=….
a4 =…
a5 =…
Ответ:
Слайд 13№ 630(а)
В арифметической прогрессии (an ) найти a2 + a9,
если
a1 + a10 = 120.
Решение:
a1+ a10 = a1 +(a1+9d)= 120,
2a1+9d= (a1+d) + (a1 +8d)=
Ответ:
Решение:
a1+ a10 = a1 +(a1+9d)= 120,
2a1+9d= (a1+d) + (a1 +8d)=
Ответ:
Слайд 14№ 632 (а)
Является ли число 12 членом арифметической прогрессии - 10;
- 8; -6; …?
Решение:
d= a2 – a1 =– 8 – (–10)=2,
a1 + (n– 1)·d = an ,
– 10 +(n– 1)·2 = 12,
Решение:
d= a2 – a1 =– 8 – (–10)=2,
a1 + (n– 1)·d = an ,
– 10 +(n– 1)·2 = 12,
Т.к. 12 – целое число, значит a12 =12.
Ответ: число 12 является 12-м членом
арифметической прогрессии.
Слайд 15Дополнительное задание
В арифметической прогрессии найти a10, если
a25 − a20 =
10 и a16 = 13.
Решение:
a25= a1 +24d, a20= a1+19d, a16= a1+15d.
(a1 +24d) – (a1+19d)=10,
a1+15d =13.
Решая эту систему, найдем , , .
Тогда a10= a1+ 9d=
Ответ:
Решение:
a25= a1 +24d, a20= a1+19d, a16= a1+15d.
(a1 +24d) – (a1+19d)=10,
a1+15d =13.
Решая эту систему, найдем , , .
Тогда a10= a1+ 9d=
Ответ:
Слайд 16Самостоятельная работа
Дидактические материалы
С - 18 «Арифметическая прогрессия»,
Варианты 1 и 2, задания 1, 2
Варианты 1 и 2, задания 1, 2
Слайд 17Итог урока
Какую последовательность называют арифметической прогрессией?
Что называют разностью арифметической прогрессии?
Как ее найти?
Какова формула n-го члена арифметической прогрессии?
Какими свойствами обладает арифметическая прогрессия?
Какова формула n-го члена арифметической прогрессии?
Какими свойствами обладает арифметическая прогрессия?
