- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Устная работа по подготовке к ОГЭ
Содержание
- 1. Презентация по математике Устная работа по подготовке к ОГЭ
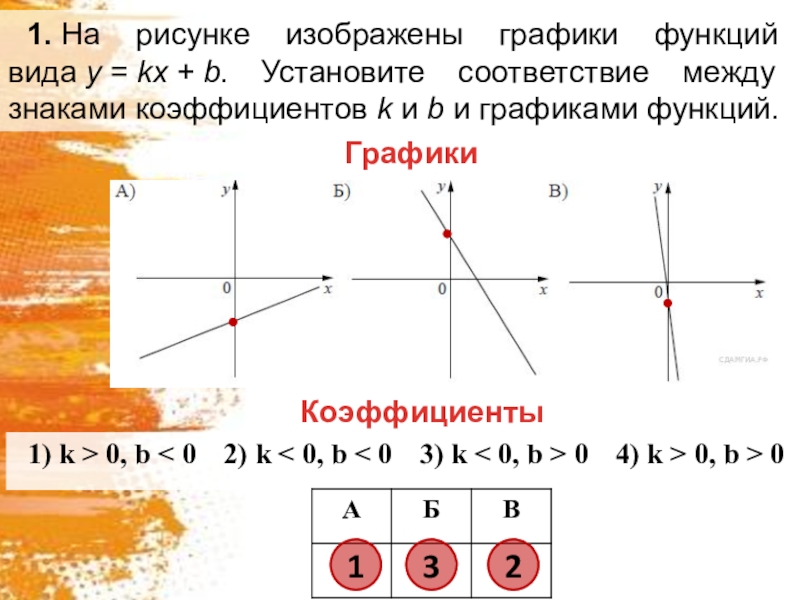
- 2. 1. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.КоэффициентыГрафики132
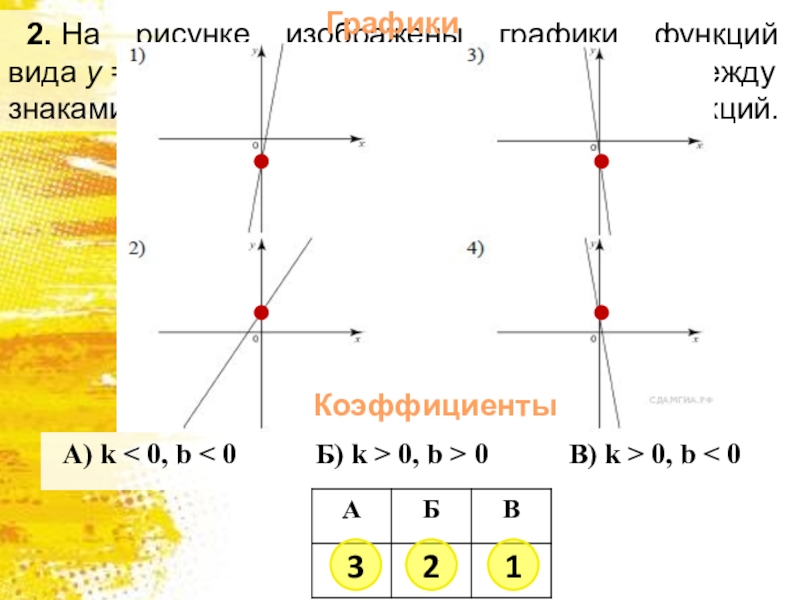
- 3. 2. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.Графики321Коэффициенты
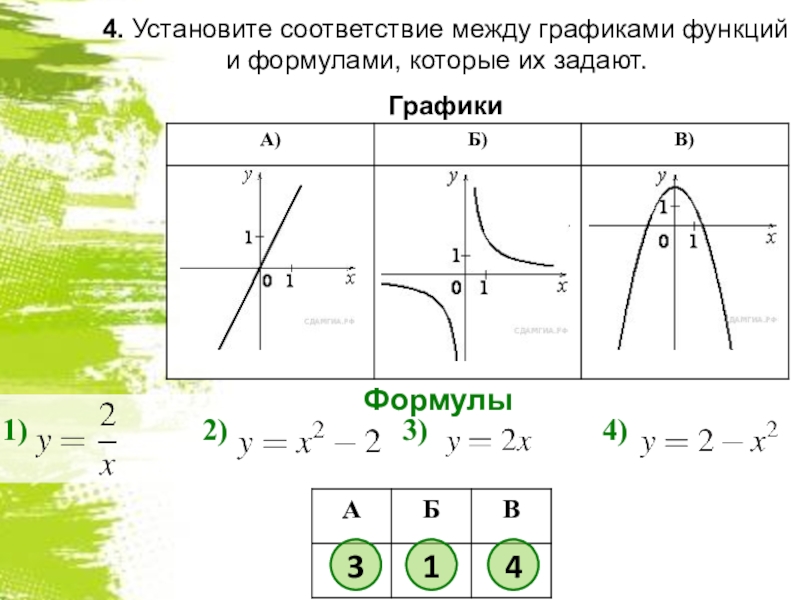
- 4. 4. Установите соответствие между графиками функций и формулами, которые их задают. ГрафикиФормулы314
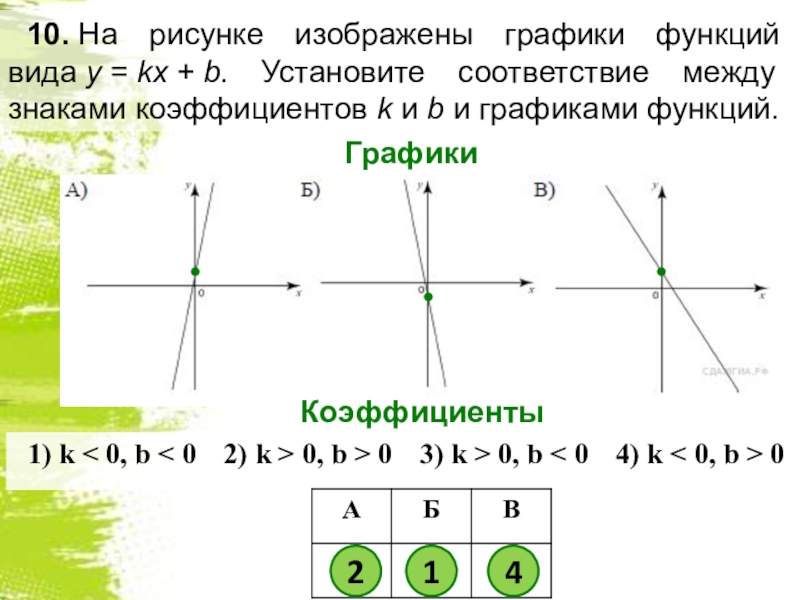
- 5. 10. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.КоэффициентыГрафики214
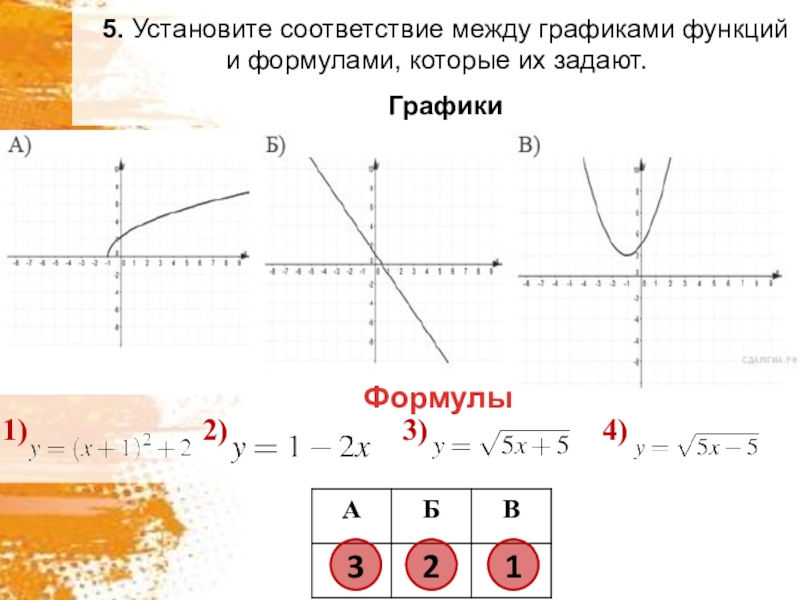
- 6. 5. Установите соответствие между графиками функций и формулами, которые их задают. ГрафикиФормулы 321
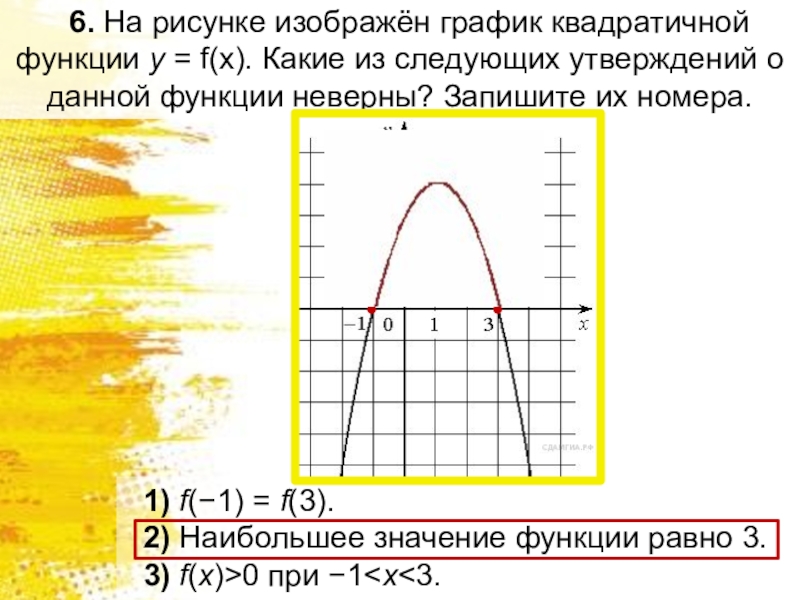
- 7. 6. На рисунке изображён график квадратичной функции y = f(x). Какие
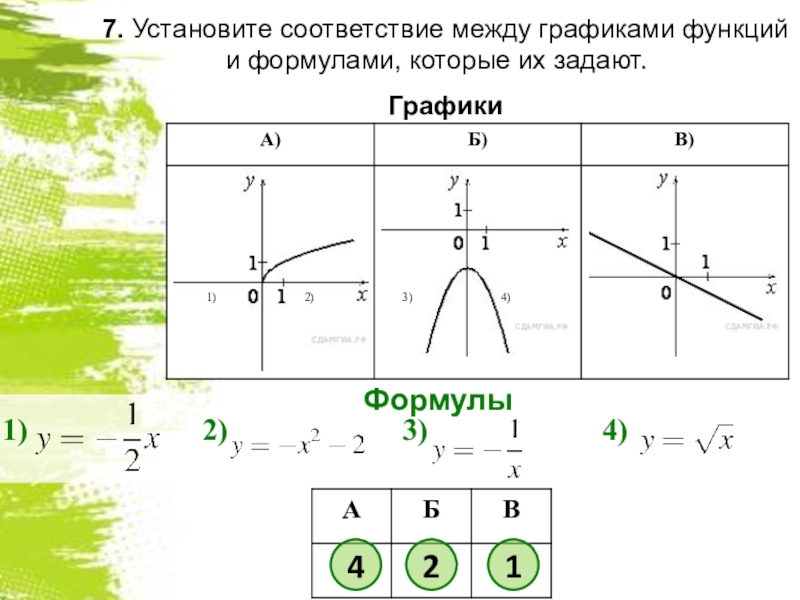
- 8. 7. Установите соответствие между графиками функций и формулами, которые их задают. ГрафикиФормулы421
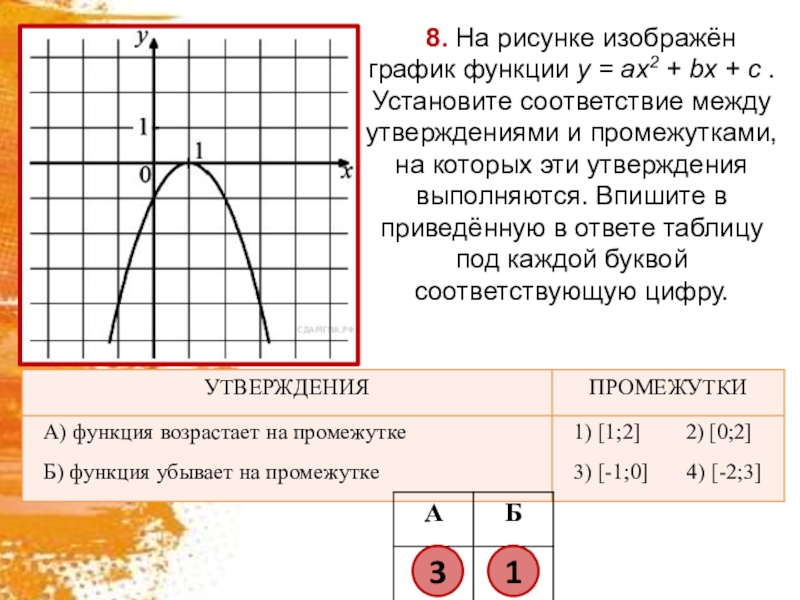
- 9. 8. На рисунке изображён график функции y = ax2 +
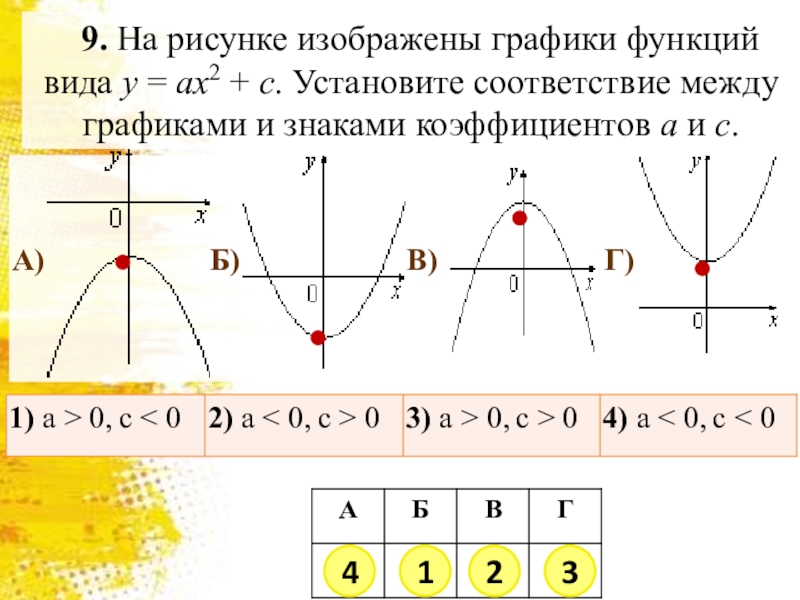
- 10. 9. На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между графиками и знаками коэффициентов a и c. 4123
- 11. 1. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.КоэффициентыГрафики132
- 12. самооценка10-9 б – «5»7-8 б – «4»5-6 б – «3»0-4 б- «2»
- 13. а)
- 14. Тема:Решение задач с помощью систем уравнений второй степени
- 15. Цель: формировать умение решать задач с помощью
- 16. №469Р е ш е н и еПусть
- 17. Домашнее задание: № 479, № 474 Сборник заданий ОГЭ В-22 №1-8
- 18. Устная работа по геометрии задание №13 ОГЭ-2016
- 19. Какие из
- 20. Какие из следующих утверждений верны? 1) Площадь многоугольника,
- 21. Какие из следующих утверждений верны? 1) Квадрат любой
- 22. Какие из следующих утверждений верны? 1) Сумма углов
- 23. Какие из следующих утверждений верны? 1) Если в
- 24. Какое из следующих утверждений верно?1) Если два
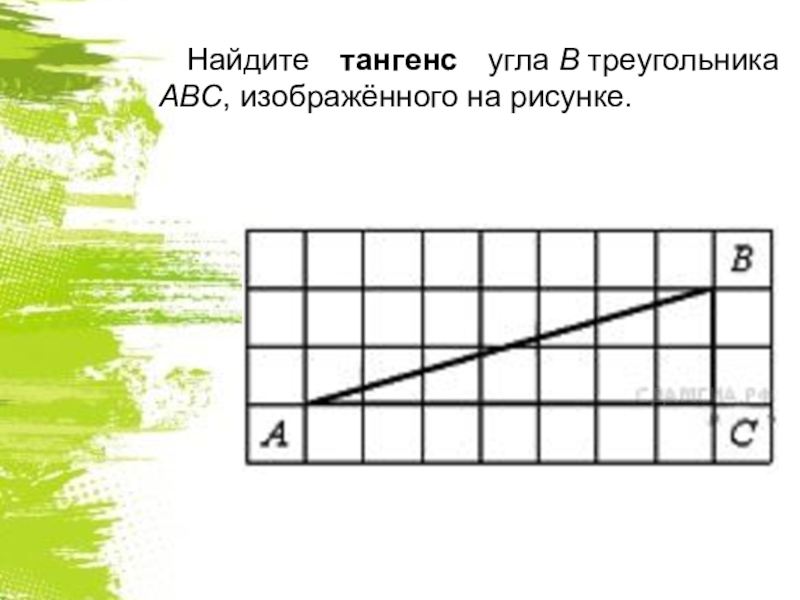
- 25. Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
- 26. Теоретический опросформулы для R, r, а
- 27. Тема урокарадианная мера углаЦели: вывести формулу длины
- 28. Отношение длины окружности к ее диаметру есть
- 29. №1 Диаметр окружности , описанной около правильного треугольника, равен 20 √3см. Вычислите периметр этого треугольника
- 30. №2 Диаметр окружности , описанной около правильного шестиугольника, равен 24см. Вычислите периметр этого шестиугольника.
- 31. Домашнее задание: изучить п.120Выполнить : №43 (2,4)
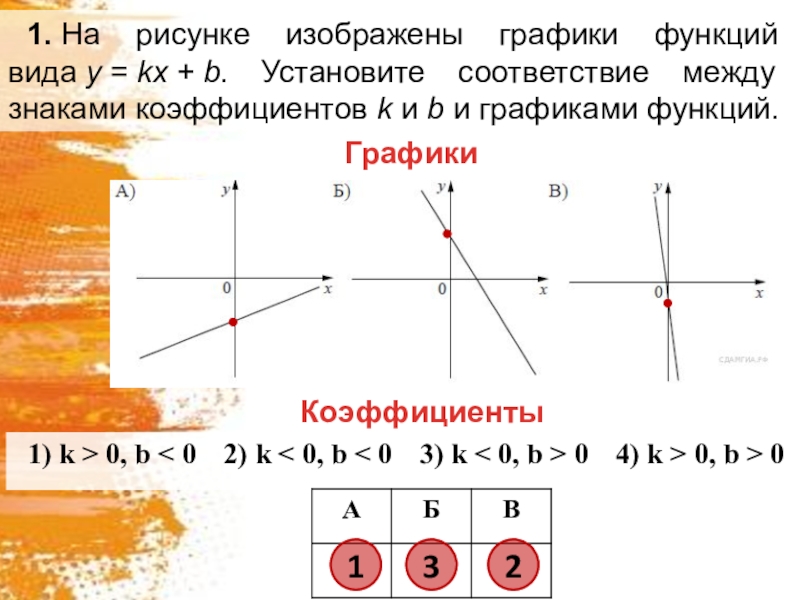
1. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.КоэффициентыГрафики132
Слайд 21. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и
графиками функций.
Коэффициенты
Графики
1
3
2
Слайд 32. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и
графиками функций.
Графики
3
2
1
Коэффициенты
Слайд 44. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
Формулы
3
1
4
Слайд 510. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и
графиками функций.
Коэффициенты
Графики
2
1
4
Слайд 65. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
Формулы
3
2
1
Слайд 76. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о
данной функции неверны? Запишите их номера.
1) f(−1) = f(3).
2) Наибольшее значение функции равно 3.
3) f(x)>0 при −1
Слайд 87. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
Формулы
4
2
1
Слайд 98. На рисунке изображён график функции y = ax2 + bx + c . Установите
соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
3
1
Слайд 109. На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между графиками и
знаками коэффициентов a и c.
4
1
2
3
Слайд 111. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и
графиками функций.
Коэффициенты
Графики
1
3
2
Слайд 13
а)
б) в)
Расстояние от пункта А до пункта В равно 60 км. Один пешеход проходит его на 2 ч быстрее, чем другой. Если пешеходы выйдут одновременно навстречу друг другу, то встретятся через 5 ч. Пусть х км/ч – скорость первого пешехода и у км/ч – скорость второго пешехода. Какая из систем уравнений соответствует условию задачи?
Расстояние от пункта А до пункта В равно 60 км. Один пешеход проходит его на 2 ч быстрее, чем другой. Если пешеходы выйдут одновременно навстречу друг другу, то встретятся через 5 ч. Пусть х км/ч – скорость первого пешехода и у км/ч – скорость второго пешехода. Какая из систем уравнений соответствует условию задачи?
Слайд 15Цель:
формировать умение решать задач с помощью систем уравнений второй степени,
совершенствовать навык решения систем уравнений второй степени, подготовка к ОГЭ
- развивать умственные способности;
- воспитывать познавательную активность и самостоятельность
- развивать умственные способности;
- воспитывать познавательную активность и самостоятельность
Слайд 16№469
Р е ш е н и е
Пусть х р. вкладчик положил
в банк под у % годовых. Через год ему было начислено х · 0,01у р.
Получим уравнение: 0,01ху = 400.
Через два года до начисления процентов на счету будет
(х + 400) р., а после начисления процентов стало
(х + 400) + (х + 400) · 0,01у р.
Получим уравнение:
х + 400 + 0,01у (х + 400) = 5832.
Составим систему уравнений:
Получим уравнение: 0,01ху = 400.
Через два года до начисления процентов на счету будет
(х + 400) р., а после начисления процентов стало
(х + 400) + (х + 400) · 0,01у р.
Получим уравнение:
х + 400 + 0,01у (х + 400) = 5832.
Составим систему уравнений:
Слайд 19 Какие из следующих утверждений верны?
1) Если
катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
2) Любые два равнобедренных треугольника подобны.
3) Любые два прямоугольных треугольника подобны.
4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.
2) Любые два равнобедренных треугольника подобны.
3) Любые два прямоугольных треугольника подобны.
4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.
Слайд 20 Какие из следующих утверждений верны?
1) Площадь многоугольника, описанного около окружности, равна
произведению его периметра на радиус вписанной окружности.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь трапеции меньше произведения суммы оснований на высоту.
4) Площадь прямоугольного треугольника меньше произведения его катетов.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь трапеции меньше произведения суммы оснований на высоту.
4) Площадь прямоугольного треугольника меньше произведения его катетов.
Слайд 21 Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме
квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
Слайд 22 Какие из следующих утверждений верны?
1) Сумма углов выпуклого четырехугольника равна 180°.
2)
Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
3) Диагонали квадрата делят его углы пополам.
4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
3) Диагонали квадрата делят его углы пополам.
4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
Слайд 23Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то
этот параллелограмм — прямоугольник.
2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
Слайд 24
Какое из следующих утверждений верно?
1) Если два угла одного треугольника равны
двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Слайд 26Теоретический опрос
формулы для R, r, а вписанных и описанных
окружностей около правильных многоугольников
Сумма углов правильного п-угольника
длина окружности
Сумма углов правильного п-угольника
длина окружности
Слайд 27Тема урока
радианная мера угла
Цели: вывести формулу длины дуги, сформировать умение применять
эту формулу при решении задач, дать понятие радианной меры
подготовка к ОГЭ
подготовка к ОГЭ
Слайд 28Отношение длины окружности к ее диаметру есть величина постоянная
Длина дуги
окружности, соответствующей центральному углу в n°
Радианная мера угла – это отношение длины соответствующей дуги к радиусу окружности:
Единица измерения – радиан.
1 радиан – это угол, у которого длина дуги равна радиусу.
1 радиан ≈57°
Радианная мера угла – это отношение длины соответствующей дуги к радиусу окружности:
Единица измерения – радиан.
1 радиан – это угол, у которого длина дуги равна радиусу.
1 радиан ≈57°
Слайд 29№1
Диаметр окружности , описанной около правильного треугольника, равен 20 √3см.
Вычислите периметр этого треугольника
Слайд 30№2
Диаметр окружности , описанной около правильного шестиугольника, равен 24см. Вычислите
периметр этого шестиугольника.
Слайд 31Домашнее задание:
изучить п.120
Выполнить : №43 (2,4) №46(1,2)
сборник
по подготовке к ОГЭ В-22 №9-13