«Макеевский промышленно-экономический колледж» Мещерякова Е.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Случайная величина. Закон распределения, числовые характеристики
Содержание
- 1. Презентация по математике Случайная величина. Закон распределения, числовые характеристики
- 2. В каждой естественной науке заключено столько истины,сколько
- 3. Домашнее заданиеОтдел технического контроля проверяет изделия на
- 4. Домашнее заданиеТри стрелка независимо друг от друга
- 5. Случайная величина. Закон распределения, числовые характеристики случайной величины
- 6. Цели занятиянаучиться выделять из множества различных случайных
- 7. План занятияПонятие случайной величины, виды.Составление закона распределения случайной величиныЧисловые характеристики случайной величиныПодведение итогов занятия
- 8. Актуализация опорных знаний студентов
- 9. Слайд 9
- 10. Понятие случайной величины. Дискретная и непрерывная случайная
- 11. Пример 1. В вашей группе 17 человек. Пусть
- 12. Пример 2. Изменение курса валют. Возможные события заключаются
- 13. Пример 3. Однократное бросание игральной кости. Возможные события
- 14. Пример 4. Расстояние, которое пролетит снаряд при
- 15. Дискретная случайная величина – случайная величина, которая
- 16. Определить вид случайной величины Время безаварийной работы
- 17. Сформулируйте определение случайной величины.Назовите виды случайных величин.В чем состоит отличие дискретной случайной величины от непрерывной.
- 18. Рассмотрим пример с дискретной случайной величиной:В денежной
- 19. Физическое описание объекта моделирования: владелец одного
- 20. Составим математическое описание объекта моделирования: зададим случайную
- 21. Выберем метод решения математического описания: Можно составить
- 22. Соответствие между возможными значениями дискретной случайной величины
- 23. Слайд 23
- 24. Контрольные вопросы.1.Что называют законом распределения дискретной случайной
- 25. Числовые характеристики случайной величиныЕсли закон распределения случайной
- 26. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности
- 27. Отклонением X—М(Х) называют разность между случайной величиной
- 28. Задача.В партии из 100 штук изделий прокатной
- 29. Слайд 29
- 30. Слайд 30
- 31. Поставить в соответствие элементы левого и правого столбиков
- 32. Домашнее заданиеПовторить все понятия теории вероятности.Знать основные формулы.Принести для банка прикладных задач свои презентации
- 33. Домашнее заданиеЗадача 1. Случайная величина X принимает
В каждой естественной науке заключено столько истины,сколько в ней есть математики. (И. Кант)Почему-то все верят в чудеса, а не в теорию вероятности
Слайд 1Случайная величина. Закон распределения, числовые характеристики случайной величины
Подготовила преподаватель математики ГПОУ
Слайд 2В каждой естественной науке заключено столько истины,
сколько в ней есть математики.
(И. Кант)
Почему-то все верят в чудеса, а не в теорию вероятности
Слайд 3Домашнее задание
Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что
изделие стандартно, равна 0.9. Найти вероятность того, что из двух проверенных наудачу взятых изделий только одно стандартное.
Решение
Пусть р=0,9 – вероятность того, что изделие стандартное,
тогда q=1-0,9=0,1 – изделие не стандартное
Из двух взятых изделий только одно стандартное (событие А - либо первое стандартное второе не стандартное, либо первое не стандартное второе стандартное):
Р(А)=0,9*0,1+0,1*0,9=0,09+0,09=0,18
Ответ: Р(А)=0,18
Решение
Пусть р=0,9 – вероятность того, что изделие стандартное,
тогда q=1-0,9=0,1 – изделие не стандартное
Из двух взятых изделий только одно стандартное (событие А - либо первое стандартное второе не стандартное, либо первое не стандартное второе стандартное):
Р(А)=0,9*0,1+0,1*0,9=0,09+0,09=0,18
Ответ: Р(А)=0,18
Слайд 4Домашнее задание
Три стрелка независимо друг от друга стреляют по одной мишени,
делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка – 0.7, для второго – 0.5, для третьего – 0.4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что попал второй стрелок.
Решение
Событие А – в мишени одна пробоина, попал второй стрелок.
q1=1-0.7=0.3, q3=1-0.4=0.6 – вероятности того, что первый и третий стрелки не попали в мишень.
Т.к. рассматриваются независимые события, то имеем
р(А)= q1*p2*q3= 0,3*0,5*0,6 = 0.09
Ответ: 0, 09
Решение
Событие А – в мишени одна пробоина, попал второй стрелок.
q1=1-0.7=0.3, q3=1-0.4=0.6 – вероятности того, что первый и третий стрелки не попали в мишень.
Т.к. рассматриваются независимые события, то имеем
р(А)= q1*p2*q3= 0,3*0,5*0,6 = 0.09
Ответ: 0, 09
Слайд 6Цели занятия
научиться выделять из множества различных случайных величин дискретные и непрерывные;
научиться
строить ряд распределения дискретной случайной величины;
уметь составлять ряд распределения дискретных случайных величин с небольшим числом значений.
ознакомиться с числовыми характеристиками случайной величины
уметь составлять ряд распределения дискретных случайных величин с небольшим числом значений.
ознакомиться с числовыми характеристиками случайной величины
Слайд 7План занятия
Понятие случайной величины, виды.
Составление закона распределения случайной величины
Числовые характеристики случайной
величины
Подведение итогов занятия
Подведение итогов занятия
Слайд 10Понятие случайной величины. Дискретная и непрерывная случайная величина
Случайной называется переменная величина,
которая может принимать те или иные значения в зависимости от случая.
Случайные величины принято обозначать заглавными буквами латинского алфавита- X, Y, Z, а их значения – соответствующими строчными буквами.
Случайные величины принято обозначать заглавными буквами латинского алфавита- X, Y, Z, а их значения – соответствующими строчными буквами.
Слайд 11Пример 1. В вашей группе 17 человек. Пусть величина Х – число студентов, находящихся
в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,17.
При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 17.
Слайд 12Пример 2. Изменение курса валют.
Возможные события заключаются в том, что стоимость
валюты примет некоторое значение в пределах от 57 до 62 рублей.
Слайд 13Пример 3. Однократное бросание игральной кости.
Возможные события заключаются в том, что
на верхней грани выпадает
Х: 1, 2, 3, 4, 5, 6.
Х: 1, 2, 3, 4, 5, 6.
Слайд 14Пример 4. Расстояние, которое пролетит снаряд при выстреле из орудия
Случайная
величина (зависит от установки прицела, силы и направления ветра, температуры и других факторов), а возможные значения этой величины принадлежат некоторому промежутку (a; b).
Слайд 15Дискретная случайная величина – случайная величина, которая принимает отдельные, изолированные возможные
значения с определенными вероятностями.
Непрерывная случайная величина – случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Непрерывная случайная величина – случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Слайд 16Определить вид случайной величины
Время безаварийной работы прокатного стана.
Расход горючего на
единицу расстояния.
Число студентов в группе.
Бросаем игральную кость один раз? Два раза? n раз?
Количество осадков, выпавших в сутки.
Выстрел по мишени.
Измерение температуры больного при обследовании.
Число студентов в группе.
Бросаем игральную кость один раз? Два раза? n раз?
Количество осадков, выпавших в сутки.
Выстрел по мишени.
Измерение температуры больного при обследовании.
Слайд 17Сформулируйте определение случайной величины.
Назовите виды случайных величин.
В чем состоит отличие дискретной
случайной величины от непрерывной.
Слайд 18Рассмотрим пример с дискретной случайной величиной:
В денежной лотерее выпущено 100 билетов.
Разыгрывается один выигрыш в 50 рублей и десять выигрышей по 1 рублю.
Найти вероятности возможного выигрыша для владельца одного лотерейного билета.
Слайд 19Физическое описание объекта моделирования:
владелец одного лотерейного билета может
либо выиграть
50 рублей,
либо выиграть 1 рубль
остаться вообще без выигрыша.
либо выиграть 1 рубль
остаться вообще без выигрыша.
Слайд 20Составим математическое описание объекта моделирования:
зададим случайную величину Х – стоимость
возможного выигрыша для владельца одного лотерейного билета.
Запишем возможные значения случайной величины X: x1=50, x2=1, x3=0.
Вычислим вероятность возможных значений случайной величины Х:
p1= p2= ,
p3=1-0,01-0,1=0,89
Запишем возможные значения случайной величины X: x1=50, x2=1, x3=0.
Вычислим вероятность возможных значений случайной величины Х:
p1= p2= ,
p3=1-0,01-0,1=0,89
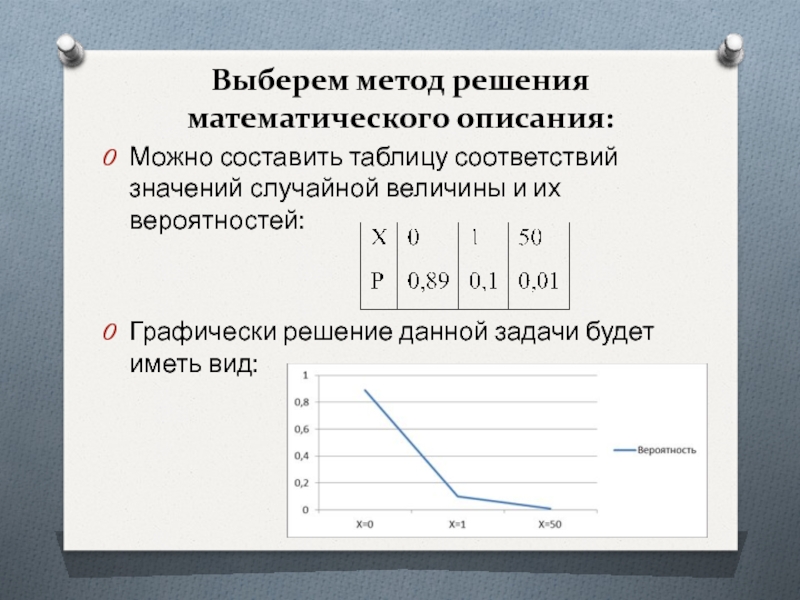
Слайд 21Выберем метод решения математического описания:
Можно составить таблицу соответствий значений случайной величины
и их вероятностей:
Графически решение данной задачи будет иметь вид:
Графически решение данной задачи будет иметь вид:
Слайд 22Соответствие между возможными значениями дискретной случайной величины и их вероятностями называют
законом распределения дискретной случайной величины.
Слайд 24Контрольные вопросы.
1.Что называют законом распределения дискретной случайной величины?
2.Какими способами можно задать
закон распределения дискретной случайной величины?
3.Что называют рядом распределения дискретной случайной величины?
3.Что называют рядом распределения дискретной случайной величины?
Слайд 25Числовые характеристики случайной величины
Если закон распределения случайной величины Х имеет вид:
то
математическим ожиданием (или средним значением)дискретной величины Х называется число:
М (X) = х1р1 + х2р2 + … + xnpn.
М (X) = х1р1 + х2р2 + … + xnpn.
Слайд 26Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений
на их вероятности
Слайд 27Отклонением X—М(Х) называют разность между случайной величиной и ее математическим ожиданиям.
Дисперсией (рассеянием)
дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X) = M[X — M(X)]2
D(X) = M[X — M(X)]2
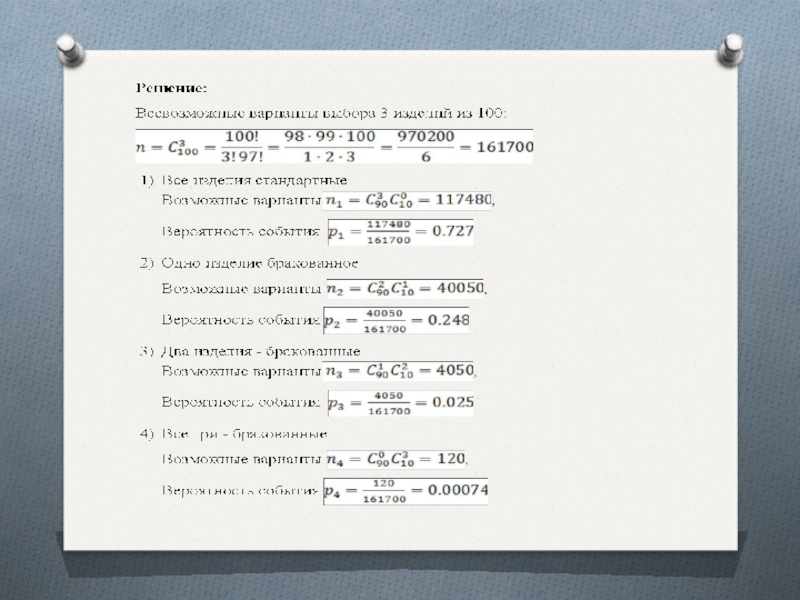
Слайд 28Задача.
В партии из 100 штук изделий прокатной продукции имеется 90 стандартных
изделий. Наудачу выбирают 3 изделия. Вычислить вероятности того, что:
Все изделия стандартные
Одно изделие бракованное
Два изделия бракованные
Все три - бракованные
Все изделия стандартные
Одно изделие бракованное
Два изделия бракованные
Все три - бракованные
Слайд 32Домашнее задание
Повторить все понятия теории вероятности.
Знать основные формулы.
Принести для банка прикладных
задач свои презентации
Слайд 33Домашнее задание
Задача 1. Случайная величина X принимает значения 0; 1; 2;
3. Известно, что вероятности равны. Написать ряд распределения дискретной случайной величины X.
Задача 2. В партии деталей 10% нестандартных. Наудачу отобраны две детали. Написать ряд распределения дискретной случайной величины Z- числа стандартных деталей среди отобранных, найти математическое ожидание и дисперсию.
Задача 2. В партии деталей 10% нестандартных. Наудачу отобраны две детали. Написать ряд распределения дискретной случайной величины Z- числа стандартных деталей среди отобранных, найти математическое ожидание и дисперсию.