Учитель математики: Коростелева Е.С.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему КОНСТРУИРОВАНИЕ И ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ ДИКТАНТОВ ПРИ ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ УЧАЩИХСЯ.
Содержание
- 1. Презентация по математике на тему КОНСТРУИРОВАНИЕ И ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ ДИКТАНТОВ ПРИ ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ УЧАЩИХСЯ.
- 2. ЦЕЛЬ : разработать систему математических диктантов
- 3. ЗАДАЧИ :получить информацию об ошибках, недочетах и
- 4. Проверка знаний по ранее изученному материалуАктуализация знаний
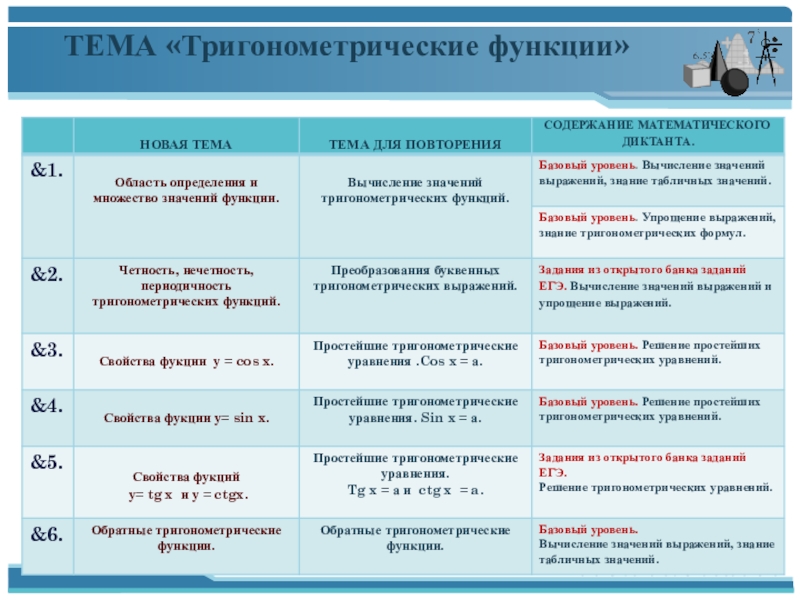
- 5. ТЕМА «Тригонометрические функции»
- 6. Математический диктант №1 по теме «Вычисление
- 7. Математический диктантПроверкаКритерий оценки«5» - 6 правильных ответов«4» - 5 правильных ответов«3» - 4 правильных ответа
- 8. Математический диктант №2 по теме «Преобразование
- 9. Математический диктантПроверкаКритерий оценки«5» - 6 правильных ответов«4» - 5 правильных ответов«3» - 4 правильных ответа
- 10. Математический диктант №3 по теме «Преобразование
- 11. Математический диктантПроверкаКритерий оценки«5» - 6 правильных ответов«4» - 5 правильных ответов«3» - 4 правильных ответа
- 12. Математический диктант №4 по теме «Простейшие тригонометрические уравнения»
- 13. Математический диктантПроверкаКритерий оценки«5» - 6 правильных ответов«4» - 5 правильных ответов«3» - 4 правильных ответа
- 14. Математический диктант №5 по теме «Простейшие тригонометрические уравнения»
- 15. Математический диктантПроверкаКритерий оценки«5» - 4 правильных ответа«4» - 3 правильных ответа«3» - 2 правильных ответа
- 16. Слайд 16
- 17. Математический диктантПроверкаКритерий оценки«5» - 6 правильных ответов«4» - 5 правильных ответов«3» - 4 правильных ответа
- 18. Этап самопроверки математического диктанта по эталону. Основной
- 19. Домашний этап локализации индивидуальных затруднений Основной
- 20. Обработка и диагностика результатов математических диктантов и
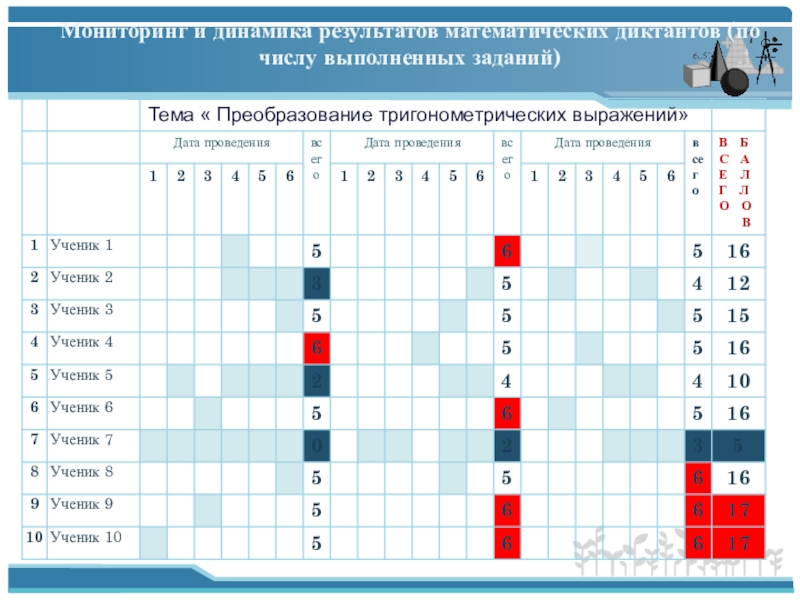
- 21. Мониторинг и динамика результатов математических диктантов (по числу выполненных заданий)
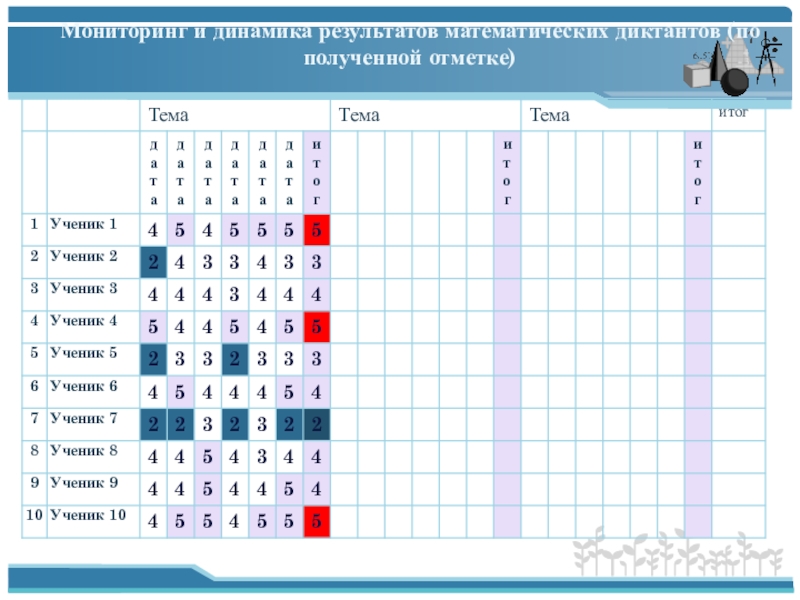
- 22. Мониторинг и динамика результатов математических диктантов (по полученной отметке)
- 23. Цель обработки и диагностики результатов математических диктантов:
- 24. ОТКРЫТЫЕ УРОКИУРОК АЛГЕБРЫ. 8 КЛАСС. «Различные приемы решения квадратных уравнений».
- 25. УРОК АЛГЕБРЫ. 10 КЛАСС. «Различные приемы решения логарифмических уравнений».ОТКРЫТЫЕ УРОКИ
- 26. Обмен опытом и выступления по данной теме.ПЕДАГОГИЧЕСКИЙ СОВЕТ. «Педагогическая диагностика. ВОПРОС … ОТВЕТ…»Март 2015. Китай.
- 27. Обмен опытом и выступления по данной теме.ВИДЕОКОНФЕРЕЦИЯ «ФГОС: вчера, сегодня, завтра. Математика.»Декабрь 2015. Китай.
- 28. « ЕСЛИ МЫ БУДЕМ УЧИТЬ СЕГОДНЯ
- 29. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.Алгебра и начала математического анализа
Слайд 1КОНСТРУИРОВАНИЕ И ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ ДИКТАНТОВ ПРИ ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ УЧАЩИХСЯ.
Средняя общеобразовательная
Слайд 2ЦЕЛЬ :
разработать систему математических диктантов для обобщающе – систематизирующего
Слайд 3ЗАДАЧИ :
получить информацию об ошибках, недочетах и пробелах в знаниях и
создать условия для включения учащихся в самостоятельную деятельность, развития навыков самооценки полученного результата и самоконтроля;
узнать , достаточно ли сформированы конкретные знания, умения и навыки для усвоения последующего учебного материала.
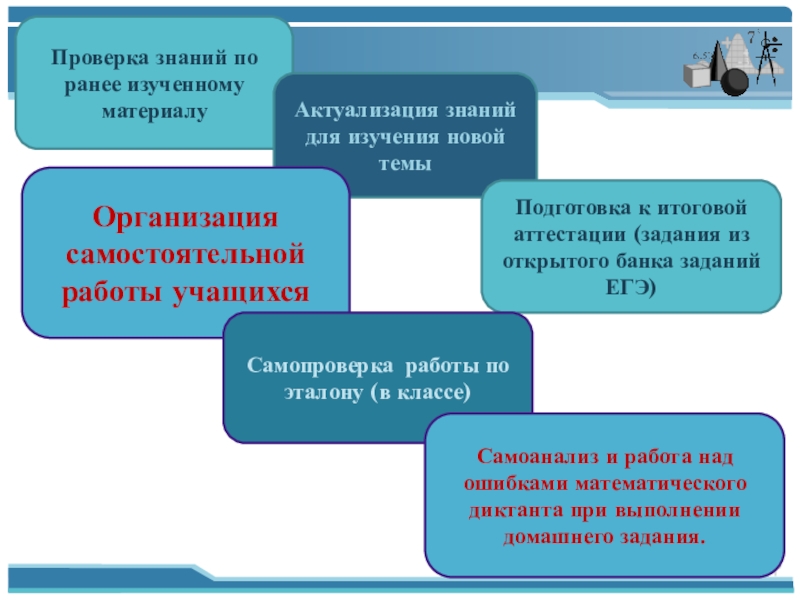
Слайд 4Проверка знаний по ранее изученному материалу
Актуализация знаний для изучения новой темы
Подготовка к итоговой аттестации (задания из открытого банка заданий ЕГЭ)
Организация самостоятельной работы учащихся
Самопроверка работы по эталону (в классе)
Самоанализ и работа над ошибками математического диктанта при выполнении домашнего задания.
Слайд 7Математический
диктант
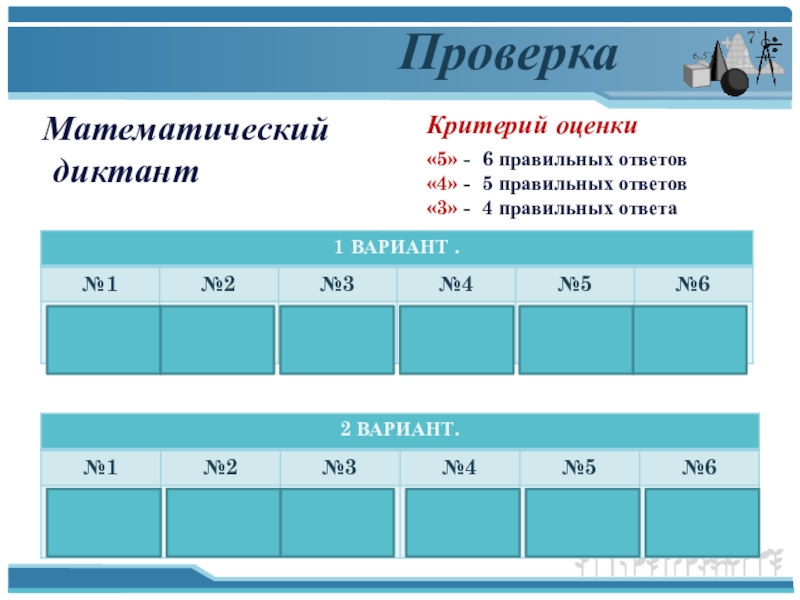
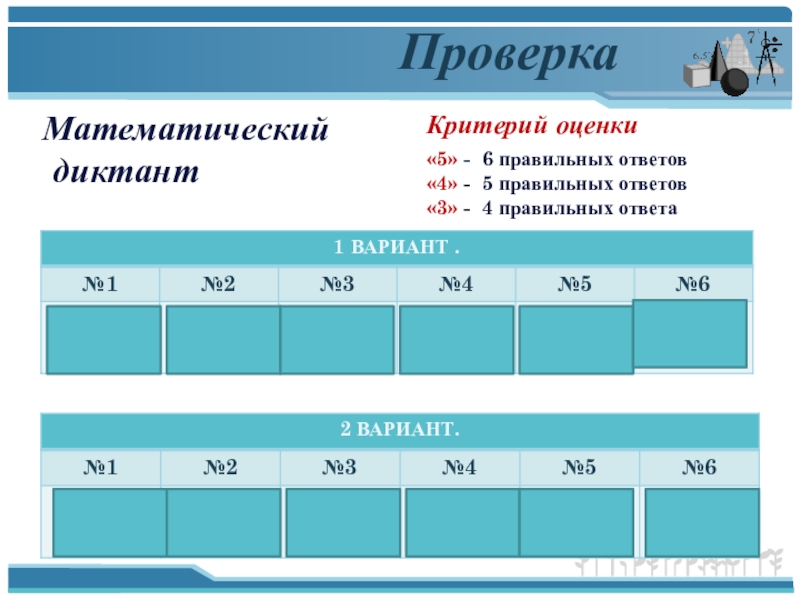
Проверка
Критерий оценки
«5» - 6 правильных ответов
«4» - 5 правильных ответов
«3»
Слайд 9Математический
диктант
Проверка
Критерий оценки
«5» - 6 правильных ответов
«4» - 5 правильных ответов
«3»
Слайд 11Математический
диктант
Проверка
Критерий оценки
«5» - 6 правильных ответов
«4» - 5 правильных ответов
«3»
Слайд 13Математический
диктант
Проверка
Критерий оценки
«5» - 6 правильных ответов
«4» - 5 правильных ответов
«3»
Слайд 15Математический
диктант
Проверка
Критерий оценки
«5» - 4 правильных ответа
«4» - 3 правильных ответа
«3»
Слайд 17Математический
диктант
Проверка
Критерий оценки
«5» - 6 правильных ответов
«4» - 5 правильных ответов
«3»
Слайд 18Этап самопроверки математического диктанта по эталону.
Основной целью этапа самопроверки по
Учащиеся
проводят самопроверку своих работ по эталону и фиксируют знаковые результаты;
фиксируют преодоление возникшего ранее затруднения;
анализируют правильность самопроверки своих работ и при необходимости – согласуют свои отметки с отметкой учителя.
Слайд 19Домашний этап локализации индивидуальных затруднений
Основной целью этапа локализации индивидуальных
Для реализации этой цели учителю необходимо
организовать мотивирование учащихся к коррекционной деятельности ( «хочу» – «надо» – «могу» ).
Учащиеся при выполнении дома работы над ошибками должны выявить места и причины собственных затруднений в выполнении математического диктанта, для этого
уточнить алгоритм исправления ошибок (алгоритм строится на предыдущих уроках);
на основе алгоритма исправления ошибок проанализировать свое решение и определить место ошибок – место затруднений;
выявить и фиксировать способы действий (алгоритмы формулы, правила и т.д.), в которых допущены ошибки, – причину затруднений.
Слайд 20Обработка и диагностика результатов математических диктантов и работ над ошибками.
С этой целью учитель ведет диагностику и мониторинг результатов математических диктантов и работ над ошибками для того ,чтобы провести подробный разбор типичных ошибок на консультации.
Анализ самостоятельной работы должен носить обучающий характер, то есть не просто констатировать количество ошибок, а производить их разбор, с тем, чтобы учащиеся смогли до конца понять вопросы, в которых сделали ошибки.
Слайд 23Цель обработки и диагностики результатов математических диктантов:
стимулировать ответственность учащихся за свои
помогать учиться на ошибках; понимать , что у них получается и в какой степени, что важно и необходимо освоить; обнаруживать, чего они не знают и что не умеют делать;
оценивать продвижение учащихся относительно самих себя, относительно своих прежних успехов и неудач;
приобщать учащихся к оцениванию своих результатов (самооценка) на основе известных им критериев.
Слайд 26Обмен опытом и выступления по данной теме.
ПЕДАГОГИЧЕСКИЙ СОВЕТ.
«Педагогическая диагностика. ВОПРОС
Март 2015. Китай.
Слайд 27Обмен опытом и выступления по данной теме.
ВИДЕОКОНФЕРЕЦИЯ
«ФГОС: вчера, сегодня, завтра.
Декабрь 2015. Китай.
Слайд 28 « ЕСЛИ МЫ БУДЕМ УЧИТЬ
СЕГОДНЯ ТАК,
КАК МЫ УЧИЛИ
МЫ УКРАДЕМ У ДЕТЕЙ ЗАВТРА».
Джон Дьюи (американский философ, психолог и педагог)
Слайд 29 ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.
Алгебра и начала математического анализа . 10 класс .
Ю.М.
Алгебра и начала математического анализа . 11 класс .
Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин. Под редакцией А.Б. Жижченко. М. : Просвещение , 2011.
С. Е. Царева «Учебная деятельность и умение учиться».
Г. К. Селевко «Современные образовательные технологии» .
Л.Ф. Батан «Организация самостоятельной деятельности учащихся в адаптивной технологии обучения».
ИНТЕРНЕТ – РЕСУРСЫ.