- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Уравнения и неравенства
Содержание
- 1. Презентация по математике Уравнения и неравенства
- 2. Цель урока: формирование навыков решения линейных неравенствЦели урока:Образовательные:вспомнить,
- 3. Решите: x – 8 = -59 –
- 4. Линейное уравнение ax + b = 0Решение ax +
- 5. Пример 1Решить уравнение : 10 – 2х
- 6. Линейные неравенства 1. ax + b > 0.
- 7. Алгоритм решения линейных неравенствПример: решить неравенство 5(х
- 8. Решить неравенство и изобразить множество его решений
- 9. Это — линейное неравенство. Переносим неизвестные
- 10. Это — линейное неравенство. Неизвестные — в
- 11. Решение неполного квадратного уравненияах2 + bx =
- 12. Формулы корней квадратного уравнения , дискриминант Корней не имеет
- 13. Теорема Виета В приведенном квадратном уравнениисумма
- 14. Разложение квадратного трехчлена на множители , где х1 и х2 корни уравнения .
- 15. Рациональные уравнения Решение рационального уравнения
- 16. Уравнения и неравенства с модулем Модуль действительного
- 17. Свойства модуля 1) Модули противоположных чисел равны |a|=|–a|.2) Квадрат модуля
- 18. Геометрический смысл модуляМодуль числа — это расстояние
- 19. ПримерРешить уравнение: |x - 3| = 4. Решение.Это
- 20. ПримерРешить неравенство: |x + 7|
- 21. ПримерРешить неравенство: |10 - x| ≥ 7. Решение.Расстояние от точки 10
- 22. Решить неравенство:|5 - 2x| ≥ 1 Множеством
- 23. Решить уравнение: |x – 1| + |x
- 24. Системы линейных неравенств Рассмотрим решение систем
- 25. Решить систему неравенств Решение. Решим каждое
- 26. Пример 2. Решить уравнение 3х2 – 12х
- 27. Пример 4. Найти решение системы уравнений
- 28. Пример 6. Найти точку пересечения прямых 2х
- 29. Выбрать один правильный ответРешить уравнение: -3-113
- 30. Выбрать один правильный ответ5х + 3 ≤ 1 – 3∙(х + 2)[-1; +∞)(-∞;-1)(-∞;-1](-∞;4]
- 31. Выбрать один правильный ответРешить уравнение: 10; 1-10
- 32. Выбрать один правильный ответРешить уравнение: х2 + 7х = 010; 1-10
- 33. Выбрать один правильный ответНайти сумму корней уравнения 18х2 – 2 = 0.-1/31/32/30
- 34. Выбрать один правильный ответРешить уравнение: х2 - 2х = 3х50; 1-50; 5
- 35. Выбрать один правильный ответРешить уравнение: другой ответ1,5–1,5; 21,5; –2
- 36. Выбрать один правильный ответ Решить уравнение 2(х –
- 37. Выбрать один правильный ответ Решить уравнение: другой ответ–3; 5–3; –5–3
- 38. Из пар чисел выберите ту, которая является
- 39. Выбрать один правильный ответ|3x + 2| < 5(-7/3; +∞)[-7/3, 1)(7/3; -1)(-7/3; 1)
- 40. Занятие окончено С П А С И Б О
- 41. 1) (3; –1) 2) (–9; 3)
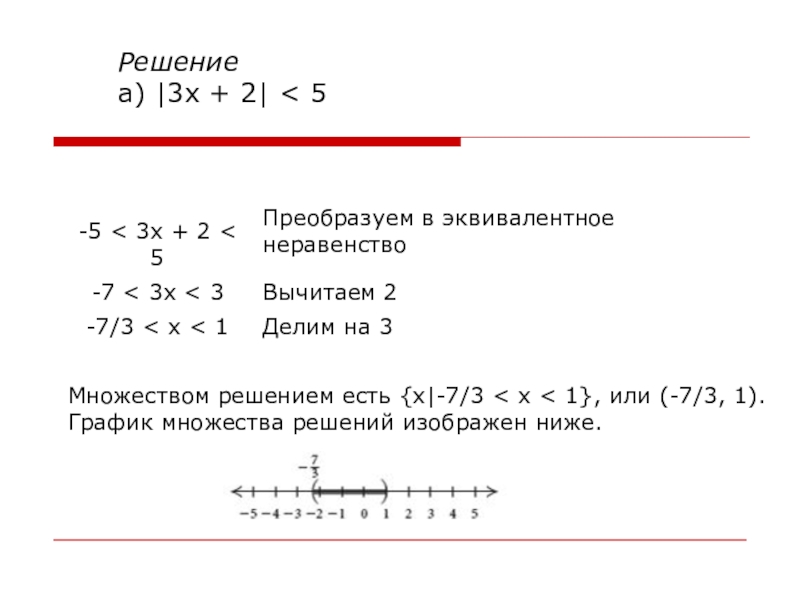
- 42. Множеством решением есть {x|-7/3 < x <
Слайд 1Уравнения и неравенства
Преподаватель математики
ГБПОУ «Cочинский торгово-технологическмй техникум»
Иванкова Н.П
Урок повторения учебного материала
Слайд 2Цель урока: формирование навыков решения линейных неравенств
Цели урока:
Образовательные:
вспомнить, что такое уранение и
вспомнить свойства числовых неравенств;
отработать навыки решения линейного, квадратного, дробного уравнения и неравенства;
Вспомнить алгоритм решения дробно-рациональных уравнений;
Уметь решать уравнения и неравенства с модулем
Воспитательные:
Воспитывать умений общаться в группах, сотрудничать и взаимообучать
Развивающие:
развитие умения самостоятельно анализировать, делать выводы;
развитие познавательного интереса;
развитие мышления учащихся;
развитие правильной речи учащихся.
Слайд 3Решите:
x – 8 = -5
9 – 2x = x + 3
a
Что значит решить уравнение?
- Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет.
Слайд 4Линейное уравнение ax + b = 0
Решение ax + b = 0,
где a, b —
х — переменная:
при a ≠ 0, х = - b/a;
при a = 0 и b = 0, х — любое число;
при a ≠ 0 и b ≠ 0 — решений нет.
Слайд 5Пример 1
Решить уравнение :
10 – 2х + 4 = 3х
5х = 15;
х = 3.
Приведем к одному знаменателю
Ответ: 3
Слайд 6Линейные неравенства
1. ax + b > 0.
2.
М - множество решений соответствующего
Неравенства ax + b < 0 и сводятся к рассмотренным умножением на -1.
Слайд 7Алгоритм решения линейных неравенств
Пример: решить неравенство 5(х – 3) > 2х
Раскрыть скобки:5х – 15 > 2х - 31.
Перенести все слагаемые с х влево, а числа вправо, меняя при этом знак на противоположный:5х – 2х > -3 + 153.
Привести подобные слагаемые:3х > 124.
Разделить обе части неравенства на число, стоящее перед х (если это число положительное, то знак неравенства не меняется; если это число отрицательное, то знак неравенства меняется на противоположный):3х > 12 : 3х > 45.
Перейти от аналитической модели х > 4 к геометрической модели: 6.
Указать множество решений данного неравенства, записав ответ:
Ответ: (4; +∞)
Слайд 8Решить неравенство и изобразить множество его решений на координатной прямой.
№1. 17
№2. 2∙(32 – 3х) ≥ 1- х
№3. 2∙(0,1х – 1) < 7 – 0,8х
Слайд 9
Это — линейное неравенство. Переносим неизвестные в одну сторону, известные
Обе части неравенства делим на число, стоящее перед иксом. Так как -2<0, знак неравенства изменяется на противоположный:
Так как неравенство строгое, 10 на числовой прямой отмечаем выколотой точкой.
Штриховка от 10 влево, на минус бесконечность.
Так как неравенство строгое и точка выколотая, 10 записываем в ответ с круглой скобкой.
Ответ:
Слайд 10Это — линейное неравенство. Неизвестные — в одну сторону, известные —
Обе части неравенства делим на число, стоящее перед иксом. Так как 10>0, знак неравенства при этом не изменяется:
Так как неравенство нестрогое, -2,3 на числовой прямой отмечаем закрашенной точкой. Штриховка от -2,3 идёт вправо, на плюс бесконечность.
Так как неравенство строгое и точка закрашенная, -2,3 в ответ записываем с квадратной скобкой.
Ответ:
Слайд 11Решение неполного квадратного уравнения
ах2 + bx = 0
Алгоритм решения:
x (aх +
x = 0 или aх + b =0
х = -b / a
Слайд 13Теорема Виета
В приведенном квадратном уравнении
сумма корней равна коэффициенту при
Если задано квадратное уравнение в общем виде , то делением уравнения на можно свести к приведенному, где ,
Слайд 15 Рациональные уравнения
Решение рационального уравнения
где P(x) и Q(x) — многочлены, сводится к решению системы:
Слайд 16Уравнения и неравенства с модулем
Модуль действительного числа
— это абсолютная
Например: |6| = 6, |-3| = 3, |-10,45| = 10,45.
Определение модуля
Слайд 17Свойства модуля
1) Модули противоположных чисел равны |a|=|–a|.
2) Квадрат модуля числа равен квадрату этого
числа |a|2 = a2.
3) Квадратный
4) Модуль числа есть число неотрицательное |a|≥ 0.
5) Постоянный положительный множитель можно выносить за знак модуля |сa|= с|a|, с > 0.
6) Если |a| = |b|, то a = ± b.
7) Модуль произведения двух (и более) чисел равен произведению их модулей |a ∙ b| = |a| ∙ |b|.
Слайд 18Геометрический смысл модуля
Модуль числа — это расстояние от нуля до данного
Например, |-5| = 5. То есть расстояние от точки -5 до нуля равно 5.
Рассмотрим простейшее уравнение |x| = 3.
Мы видим, что на числовой прямой есть две точки, расстояние
от которых до нуля равно трём. Это точки 3 и -3.
Значит, у уравнения |x| = 3 есть два решения: x = 3 и x = -3
Геометрический смысл модуля разности величин — это расстояние между ними. Например, геометрический смысл выражения |x – a| — длина отрезка координатной оси, соединяющего точки с абсциссами х и а.
Слайд 19Пример
Решить уравнение: |x - 3| = 4. Решение.
Это уравнение можно прочитать так:
расстояние от точки х до точки 3 равно 4.
С помощью графического метода можно
определить, что уравнение имеет два
решения: -1 и 7.
Слайд 21Пример
Решить неравенство: |10 - x| ≥ 7.
Решение.
Расстояние от точки 10 до точки х больше или равно
Ответ: (-∞; 3] υ [17, +∞).
Слайд 22Решить неравенство:
|5 - 2x| ≥ 1
Множеством решением есть {x|x ≤ 2 или x
или (-∞, 2] [3, ∞) .
График множества решений изображен ниже.
Слайд 23Решить уравнение: |x – 1| + |x – 2|= 1.
Решение.
x –
2х = 4 - 2х = -2
х = 2 х = 1
Ответ: 1; 2.
Слайд 24Системы линейных неравенств
Рассмотрим решение систем линейных неравенств на примерах.
Решение. Решим каждое из неравенств системы:
Изобразив на одной координатной прямой (рис. 1) оба точечных множества, составляющих последнюю систему, получаем ответ примера.
Ответ:
Слайд 25Решить систему неравенств
Решение.
Решим каждое из неравенств системы:
Изобразив на одной координатной прямой оба точечных множества, составляющих последнюю систему, получаем ответ примера.
Ответ:
Слайд 26Пример 2.
Решить уравнение 3х2 – 12х + 1 = 4х
Решение.
Перенесем все слагаемые в левую часть и приведем подобные,
получим: 5х2 – 16х + 3 = 0.
Используем способ решения квадратного уравнения
По теореме, обратной к теореме Виета:
х1х2 = 5·3 = 15х1 + х2 = 16
Подбором получим: aх1 = 15; aх2 = 1,
тогда х1 = 15/5 = 3; х2 = 1/5 = 0,2.
Ответ:
0,2 ; 3.
Слайд 27Пример 4.
Найти решение системы уравнений
1) (-15; 20) 2)
Решение.
Решим систему способом сложения .
Для этого сначала перепишем систему, чтобы переменные стояли
друг под другом:
Умножив первое уравнение системы на 2 и, сложив его со вторым,
получим:
Из предложенных ответов верным является 4).
Слайд 28Пример 6. Найти точку пересечения прямых 2х + 3у = 8 и 3х – 2у
1) (-2;4) 2) (-1;3) 3) (-1;-2)4) (1;2)
Решение.
Координатами искомой точки будет решение системы уравнений, задающих пересекающиеся прямые:
Следовательно, правильный ответ приведен под номером 4.
Слайд 36Выбрать один правильный ответ
Решить уравнение
2(х – 3) – 4х2 = х –
11;
5/8
другой ответ
1; -5/8
Слайд 38
Из пар чисел выберите ту, которая является решением системы уравнений:
(3; –1)
(–9; 3)
(2; 1)
(1; 2)
Слайд 411) (3; –1) 2) (–9; 3) 3) (2; 1)
Решение.
Подставим каждую из заданных пар чисел в систему уравнений и проверим, обращается ли каждое уравнение системы в верное равенство.
(3; –1): 3) (2; 1):
2) (–9; 3): 4) (1; 2)
Из предложенных ответов верным является 3).
Слайд 42Множеством решением есть {x|-7/3 < x < 1}, или (-7/3, 1).
Решение
a) |3x + 2| < 5


















![Презентация по математике Уравнения и неравенства ПримерРешить неравенство: |10 - x| ≥ 7. Решение.Расстояние от точки 10 до точки х больше или равно ПримерРешить неравенство: |10 - x| ≥ 7. Решение.Расстояние от точки 10 до точки х больше или равно семи. Ответ: (-∞; 3] υ [17,](/img/thumbs/3668df231e5c3a0a3fe54f463d774b2a-800x.jpg)
![Презентация по математике Уравнения и неравенства Решить неравенство:|5 - 2x| ≥ 1 Множеством решением есть {x|x ≤ Решить неравенство:|5 - 2x| ≥ 1 Множеством решением есть {x|x ≤ 2 или x ≥ 3}, или (-∞, 2]](/img/thumbs/da273c7852d6a05eda5d3d540e768f8b-800x.jpg)







[-1; +∞)(-∞;-1)(-∞;-1](-∞;4]](/img/thumbs/1975d459ab368bef89b7eddf55c3b055-800x.jpg)