- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Уравнение касательной
Содержание
- 1. Презентация по математике Уравнение касательной
- 2. ЦЕЛЬ УРОКА: НА ОСНОВЕ РЕШЕНИЯ ЗАДАЧ ВЫВЕСТИ УСЛОВИЕ КАСАНИЯ ПРЯМОЙ С ГРАФИКОМ ФУНКЦИИ У=F(X)
- 3. СОГЛАСНЫ ЛИ ВЫ С УТВЕРЖДЕНИЕМ:«Касательная – это прямая, имеющая с данной кривой одну общую точку»
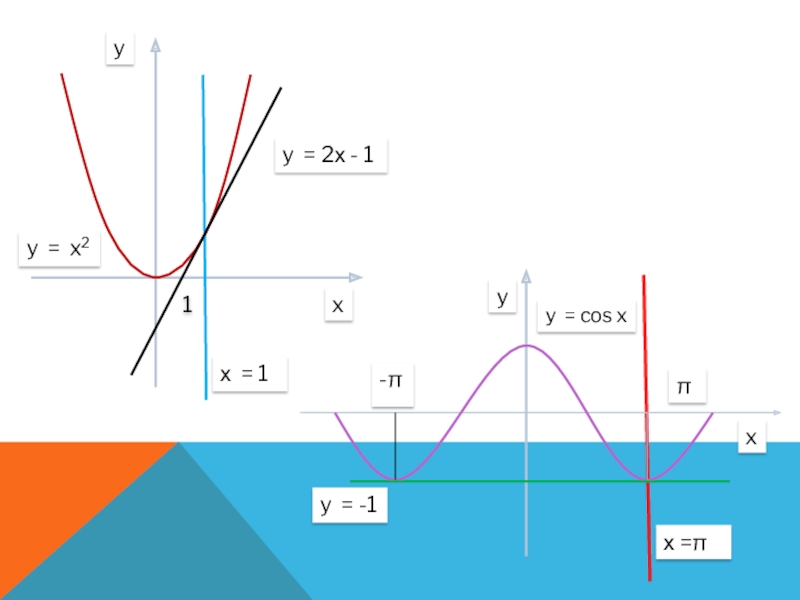
- 4. 1y = -1xyy = cos x-ππxyy = x2х = 1y = 2х - 1х =π
- 5. ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=F(Х)
- 6. Касательной к графику функции f, дифференцируемой
- 7. Угловой коэффициент касательной к графику функции в
- 8. Слайд 8
- 9. В каких точках графика касательная к
- 10. При каких значениях аргумента производная функции,
- 11. УРАВНЕНИЕ ВИДА У=F(А)+F’(А)(Х-А) ЯВЛЯЕТСЯ УРАВНЕНИЕМ КАСАТЕЛЬНОЙ К
- 12. 1. Если задана точка касанияНаписать уравнение касательной
- 13. 1. Написать уравнения всех касательных к графику
- 14. Написать уравнения всех касательных к графику
- 15. Условия параллельности и перпендикулярностидвух прямых. Пусть
- 16. 1. Составить уравнение касательной к графику функции f(x) =x2+4x+1, перпендикулярной прямой y = -1/4x+8.
- 17. Условие касания Прямая у=kх+b является
ЦЕЛЬ УРОКА: НА ОСНОВЕ РЕШЕНИЯ ЗАДАЧ ВЫВЕСТИ УСЛОВИЕ КАСАНИЯ ПРЯМОЙ С ГРАФИКОМ ФУНКЦИИ У=F(X)
Слайд 3СОГЛАСНЫ ЛИ ВЫ С УТВЕРЖДЕНИЕМ:
«Касательная – это прямая, имеющая с данной
кривой одну общую точку»
Слайд 5ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=F(Х)
Пусть дана
некоторая кривая и точка Р на ней. Возьмем на этой кривой другую точку Р1 и проведем прямую через точки Р и Р1. Эту прямую называют секущей. Будем приближать точку Р1 к Р. Положение секущей РР1 будет меняться (стремиться к точки Р) предельное положение прямой РР1 и будет касательной к кривой в точке Р.
Слайд 6Касательной к графику функции f, дифференцируемой в точке х0
, называется прямая, проходящая через точку (x0, f(x0)) и имеющая угловой коэффициент k= f '(х0).
ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ
Слайд 7Угловой коэффициент касательной к графику функции в точке равен значению производной
в этой точке.
kкас. = f /(x0) = tgα
kкас. = f /(x0) = tgα
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
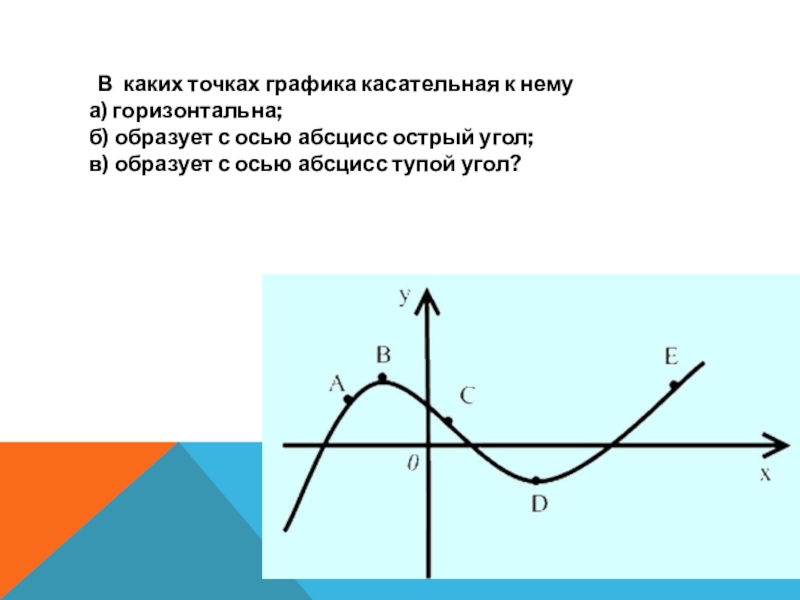
Слайд 9 В каких точках графика касательная к нему
а) горизонтальна;
б) образует
с осью абсцисс острый угол;
в) образует с осью абсцисс тупой угол?
в) образует с осью абсцисс тупой угол?
Слайд 10
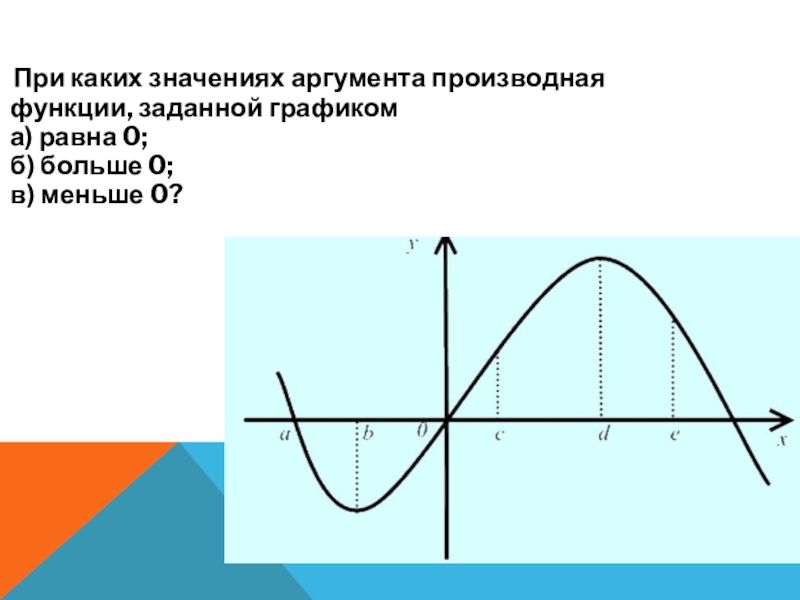
При каких значениях аргумента производная функции, заданной графиком
а) равна
0;
б) больше 0;
в) меньше 0?
Слайд 11УРАВНЕНИЕ ВИДА У=F(А)+F’(А)(Х-А) ЯВЛЯЕТСЯ УРАВНЕНИЕМ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ.
Уравнение вида у=f(хо)+f’
(хо)(х-хо) является уравнением касательной к графику функции.
Слайд 121. Если задана точка касания
Написать уравнение касательной к графику
функции f(x) = x3 – 3x – 1 в
точке М с абсциссой 3.
2. По ординате точки касания.
Написать уравнение касательной в точке
графика с ординатой y0 = 1.
Слайд 131. Написать уравнения всех касательных к графику функции f(x) = x2 + 4x + 6 ,
проходящих через точку М (-3; -1).
2. Правильно ли составлено уравнение касательной к графику функции f(x) = x3-3x2+1, если угловой коэффициент касательной k = -3, y = -3x+7?
2. Правильно ли составлено уравнение касательной к графику функции f(x) = x3-3x2+1, если угловой коэффициент касательной k = -3, y = -3x+7?
Слайд 14 Написать уравнения всех касательных к графику функции
F(x) =
х2 +4х+6 проходящих через точку М(-3;-1).
Решение. 1. Точка М(-3;-1) не является точкой касания, так как f(-3)=3.
2. а – абсцисса точки касания.
3. Найдем f(a): f(a) = a 2+4a+6.
4. Найдем f ’(x) и f ’(a): f ’(x)=2x+4, f ’(a)=2a+4.
5. Подставим числа а, f(a), в общее уравнение касательной
у= f(a)+ f’(a)(x–a): y=a2+4a+6+(2a+4)(x–a) – уравнение касательной.
Так как касательная проходит через точку М(-3;-1), то -1=a2+4a+6+(2a+4)(-3–a), a2+6a+5=0, a=-5 или a=-1.
Если a=-5, то y=-6x–19 – уравнение касательной.
Если a=-1, y=2x+5 – уравнение касательной.
Ответ: y=-6x–19, y=2x+5.
Решение. 1. Точка М(-3;-1) не является точкой касания, так как f(-3)=3.
2. а – абсцисса точки касания.
3. Найдем f(a): f(a) = a 2+4a+6.
4. Найдем f ’(x) и f ’(a): f ’(x)=2x+4, f ’(a)=2a+4.
5. Подставим числа а, f(a), в общее уравнение касательной
у= f(a)+ f’(a)(x–a): y=a2+4a+6+(2a+4)(x–a) – уравнение касательной.
Так как касательная проходит через точку М(-3;-1), то -1=a2+4a+6+(2a+4)(-3–a), a2+6a+5=0, a=-5 или a=-1.
Если a=-5, то y=-6x–19 – уравнение касательной.
Если a=-1, y=2x+5 – уравнение касательной.
Ответ: y=-6x–19, y=2x+5.
Слайд 15 Условия параллельности и перпендикулярности
двух прямых.
Пусть даны две прямые:
у1=k1x+b1
и у2=k2x+b2.
Если k1= k2, то прямая у1 параллельна у2.
Если k1⋅k2= –1, то данные прямые взаимно перпендикулярны
Если k1= k2, то прямая у1 параллельна у2.
Если k1⋅k2= –1, то данные прямые взаимно перпендикулярны
Слайд 161. Составить уравнение касательной к графику
функции f(x) =x2+4x+1, перпендикулярной
прямой y
= -1/4x+8.
Слайд 17Условие касания
Прямая у=kх+b является касательной к графику функции
у=f(x) тогда и только тогда, когда существует хотя бы одна точка касания а, для которой выполняется система
f(a)=ka+b,
f ’(a)=k.
f(a)=ka+b,
f ’(a)=k.