- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Тригонометрические уравнения
Содержание
- 1. Презентация по математике Тригонометрические уравнения
- 2. The functions cosΘ° and sinΘ° have the
- 3. The function tanΘ° has the following properties
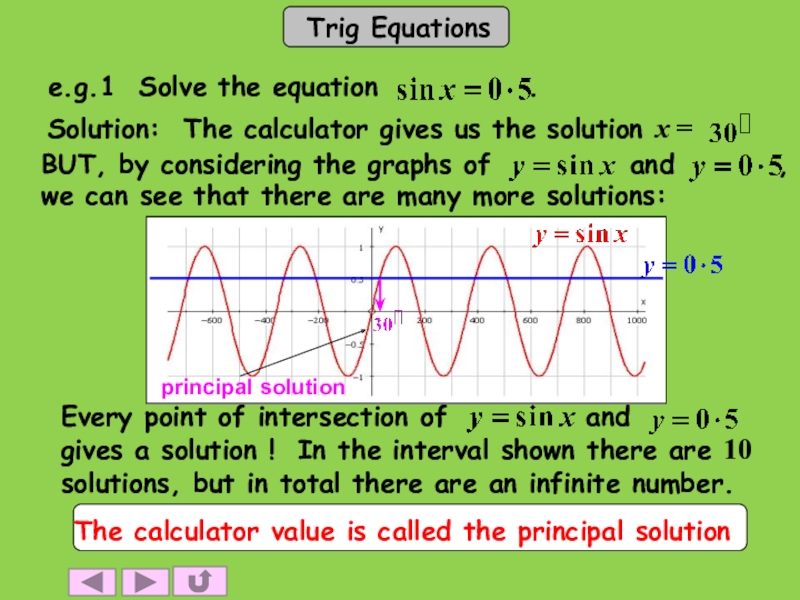
- 4. Solution: The calculator gives us the solution x =
- 5. We will adapt the question to:There are
- 6. Solution: The first answer from the calculator
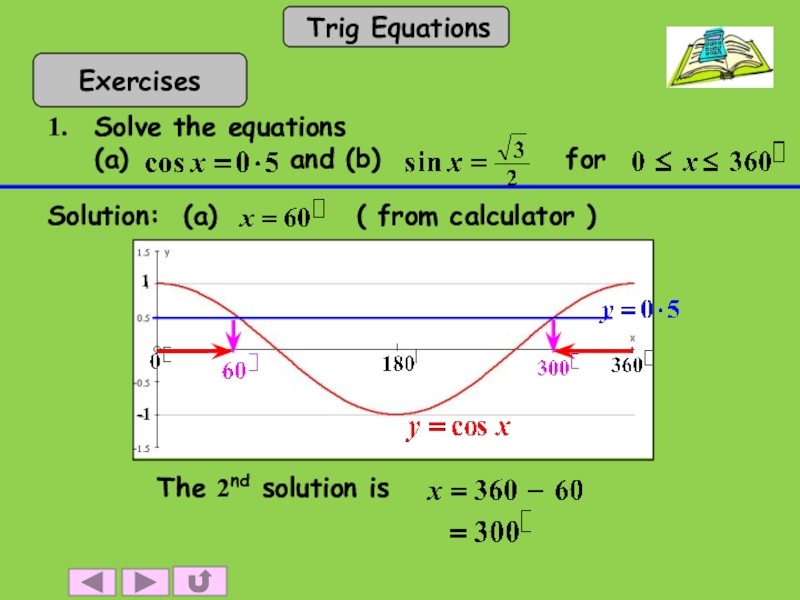
- 7. Find the principal solution from a calculator.
- 8. Solve the equations (a)
- 9. Слайд 9
- 10. The 2nd solution is
- 11. Слайд 11
- 12. and keep adding . . .
- 13. Слайд 13
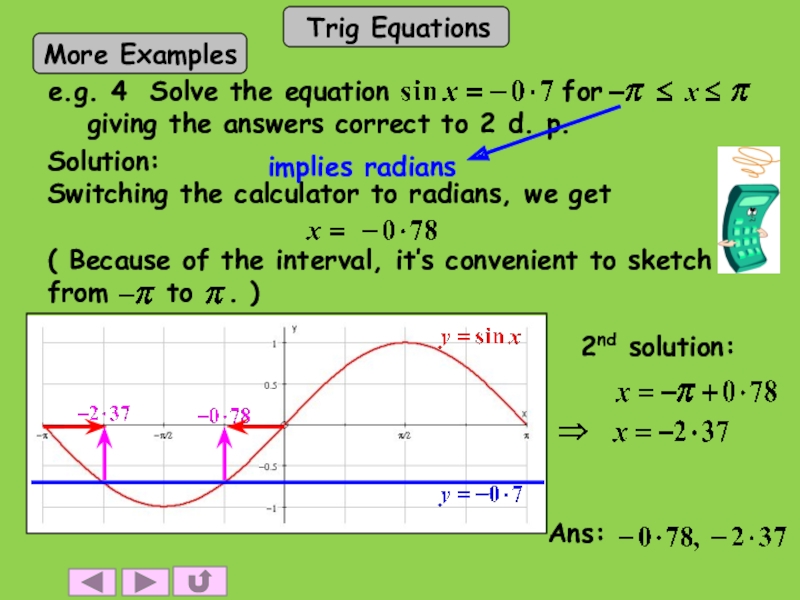
- 14. Switching the calculator to radians, we getSolution:implies radians2nd solution:
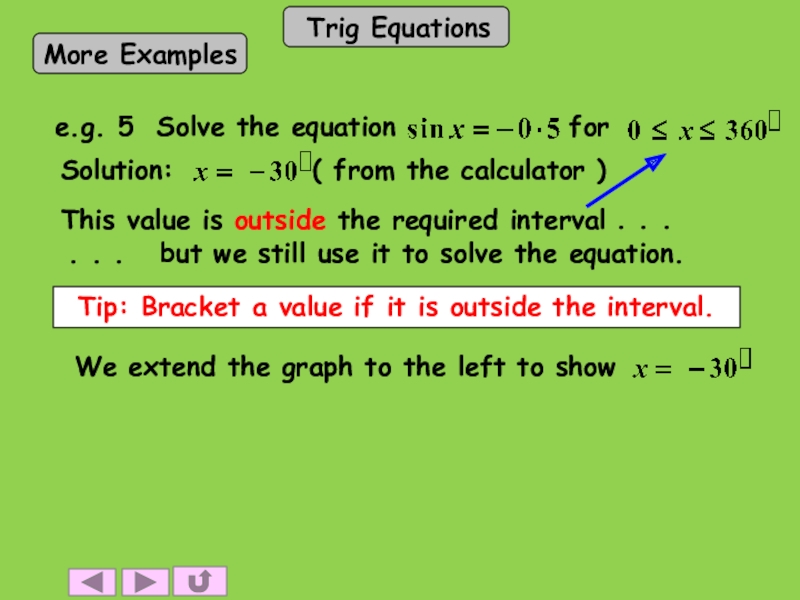
- 15. This value is outside the required interval
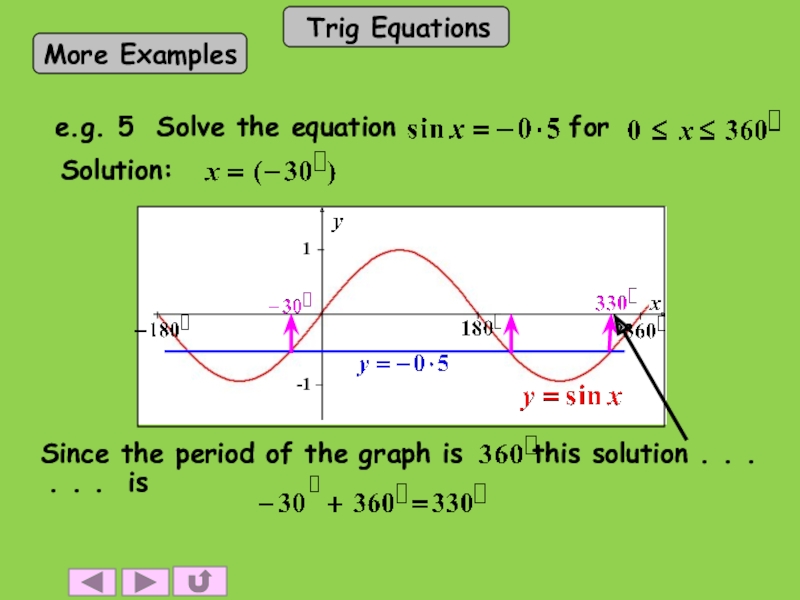
- 16. . . . is Solution:
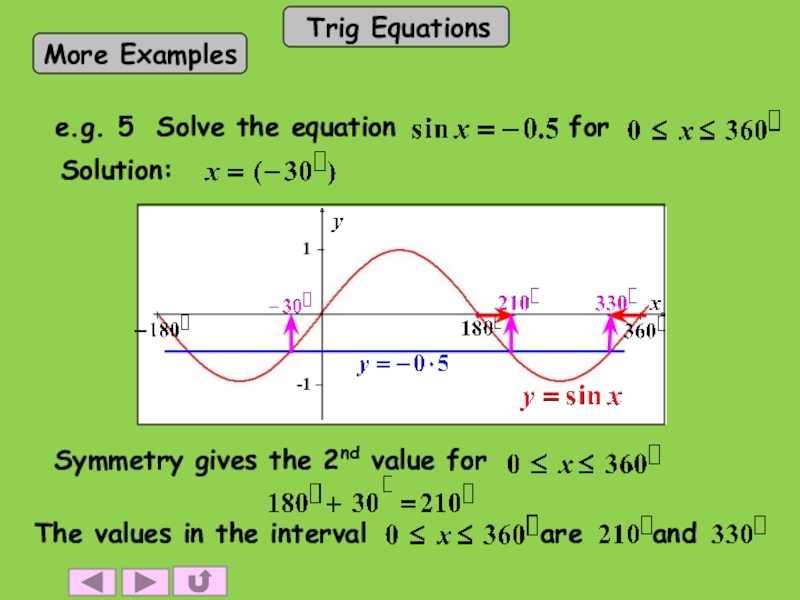
- 17. Solution:
- 18. Слайд 18
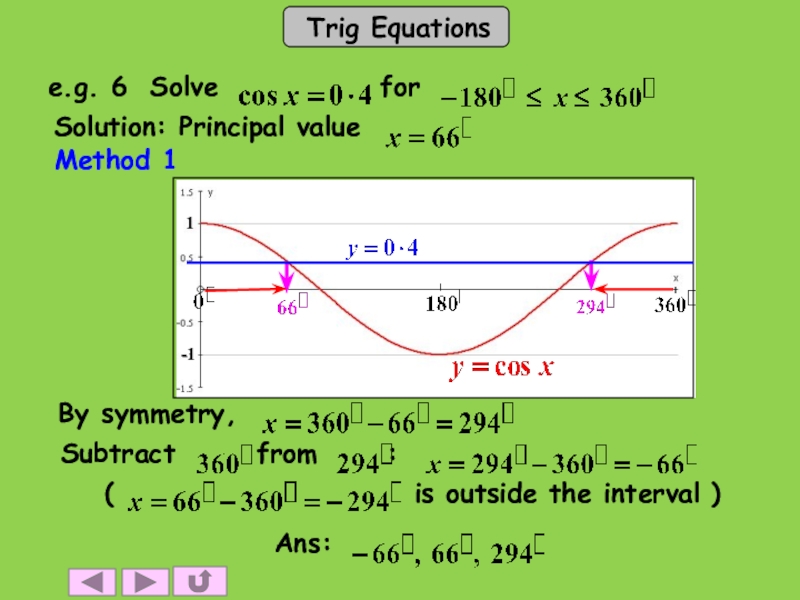
- 19. Method 1
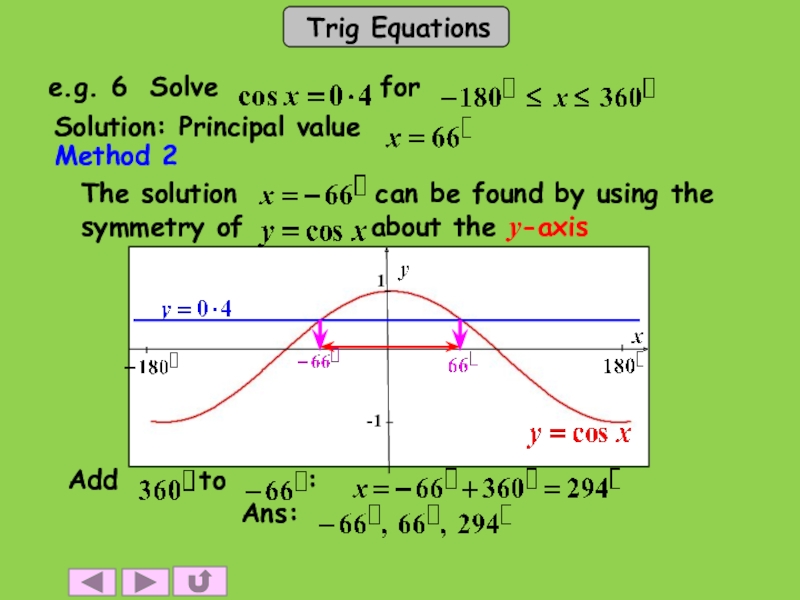
- 20. Method 2
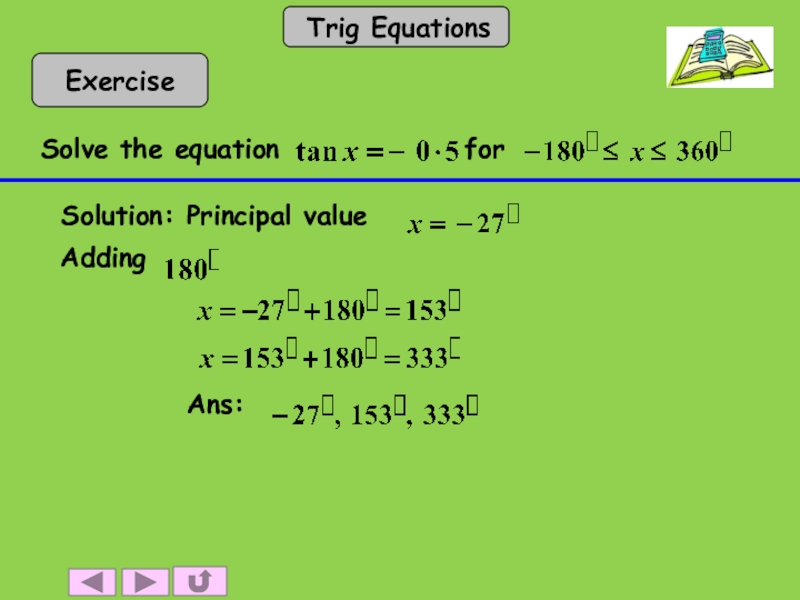
- 21. Find the principal value from the calculator.
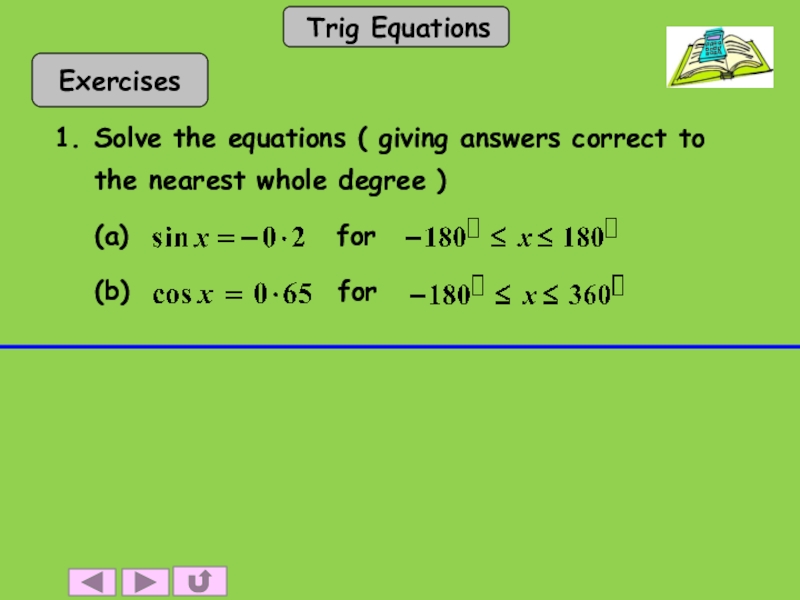
- 22. 1. Solve the equations ( giving answers correct
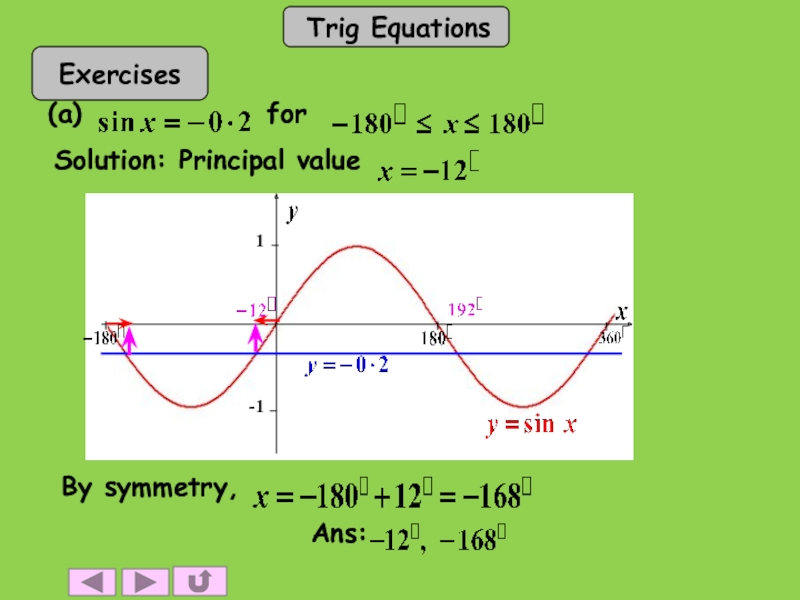
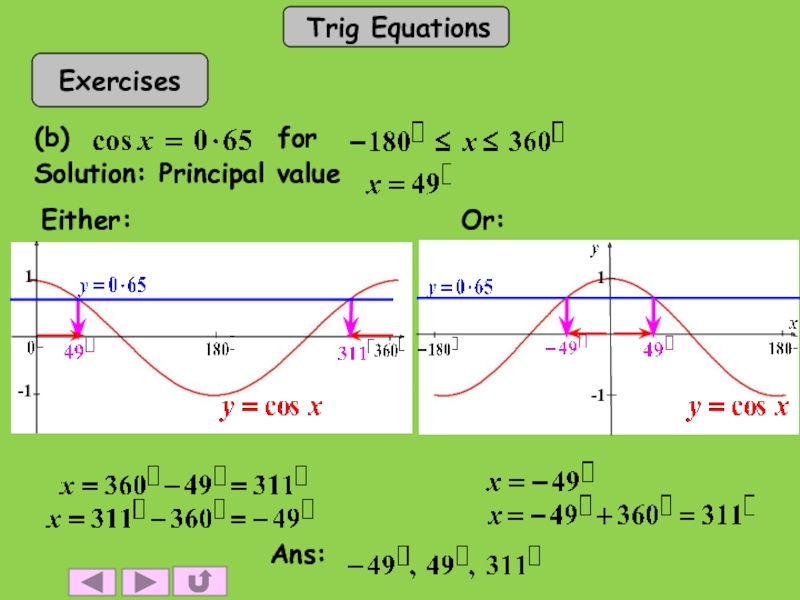
- 23. (a) for
- 24. Either:Or:
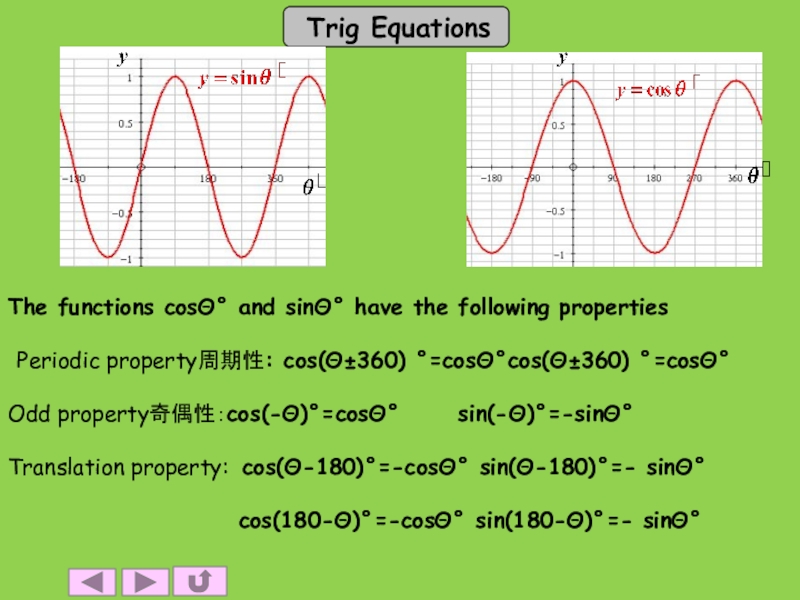
The functions cosΘ° and sinΘ° have the following properties Periodic property周期性: cos(Θ±360) °=cosΘ°cos(Θ±360) °=cosΘ°Odd property奇偶性:cos(-Θ)°=cosΘ° sin(-Θ)°=-sinΘ°Translation property: cos(Θ-180)°=-cosΘ° sin(Θ-180)°=- sinΘ° cos(180-Θ)°=-cosΘ° sin(180-Θ)°=- sinΘ°
Слайд 2The functions cosΘ° and sinΘ° have the following properties
Periodic property周期性:
cos(Θ±360) °=cosΘ°cos(Θ±360) °=cosΘ°
Odd property奇偶性:cos(-Θ)°=cosΘ° sin(-Θ)°=-sinΘ°
Translation property: cos(Θ-180)°=-cosΘ° sin(Θ-180)°=- sinΘ°
cos(180-Θ)°=-cosΘ° sin(180-Θ)°=- sinΘ°
Odd property奇偶性:cos(-Θ)°=cosΘ° sin(-Θ)°=-sinΘ°
Translation property: cos(Θ-180)°=-cosΘ° sin(Θ-180)°=- sinΘ°
cos(180-Θ)°=-cosΘ° sin(180-Θ)°=- sinΘ°
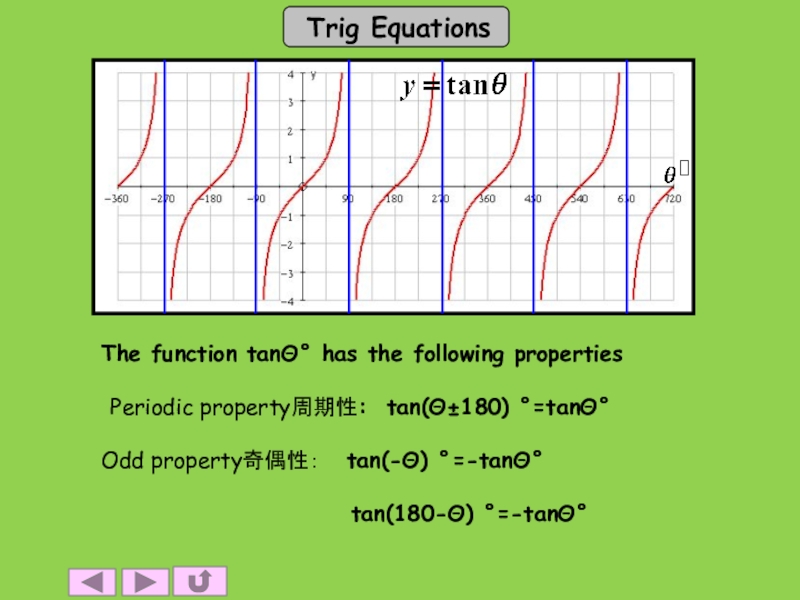
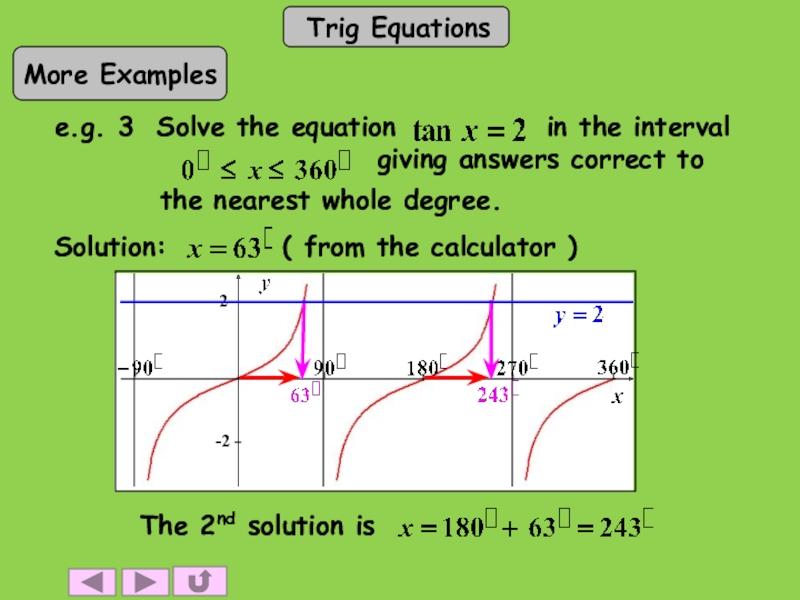
Слайд 3The function tanΘ° has the following properties
Periodic property周期性: tan(Θ±180) °=tanΘ°
Odd
property奇偶性: tan(-Θ) °=-tanΘ°
tan(180-Θ) °=-tanΘ°
tan(180-Θ) °=-tanΘ°
Слайд 5We will adapt the question to:
There are 2 solutions.
The symmetry of
the graph . . .
. . . shows the 2nd solution is
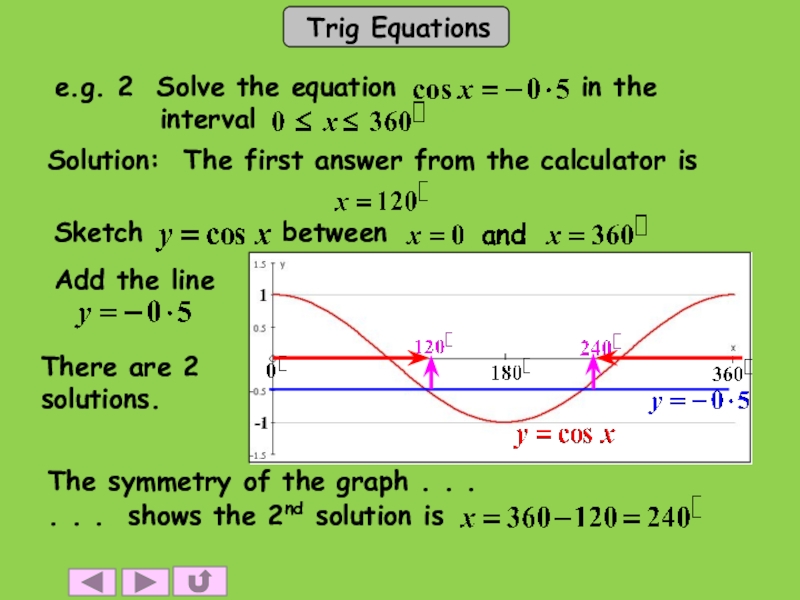
Слайд 6Solution: The first answer from the calculator is
There are 2 solutions.
The
symmetry of the graph . . .
. . . shows the 2nd solution is
Слайд 7Find the principal solution from a calculator.
Find the 2nd solution
using symmetry
or
Draw the line y = c.
Слайд 15This value is outside the required interval
. . .
. . . but we still use it to solve the equation.
Tip: Bracket a value if it is outside the interval.
Слайд 21Find the principal value from the calculator.
Sketch the graph of
the trig function showing at least one complete cycle and including the principal value.
Find a 2nd solution using the graph.
Find the principal value from the calculator.