- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике. Три способа решения задачи С14.
Содержание
- 1. Презентация по математике. Три способа решения задачи С14.
- 2. 14.(1) В правильной треугольной призме ????1?1?1 все
- 3. 14.(1) В правильной треугольной призме ????1?1?1 все
- 4. 14. (1)В правильной треугольной призме ????1?1?1 все
- 5. 14. (1)В правильной треугольной призме ????1?1?1 все
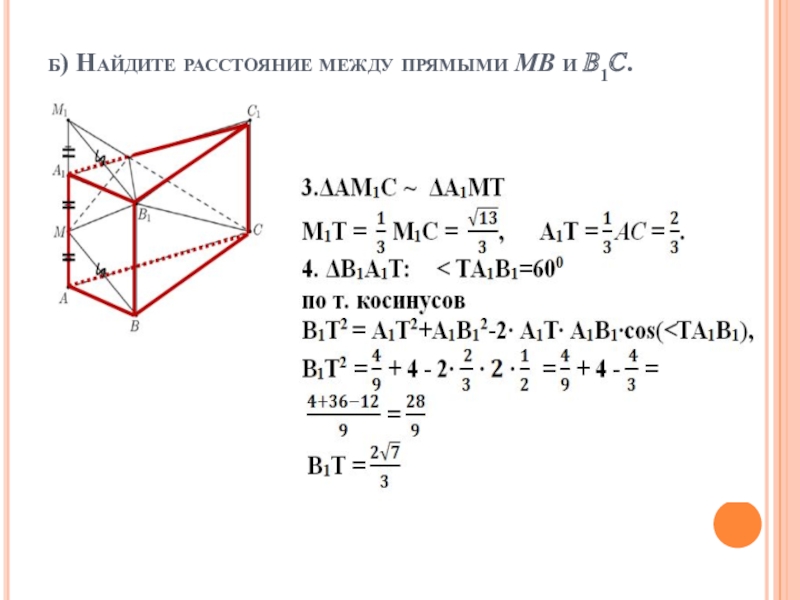
- 6. б) Найдите расстояние между прямыми MB и ?1?.
- 7. б) Найдите расстояние между прямыми MB и ?1?.
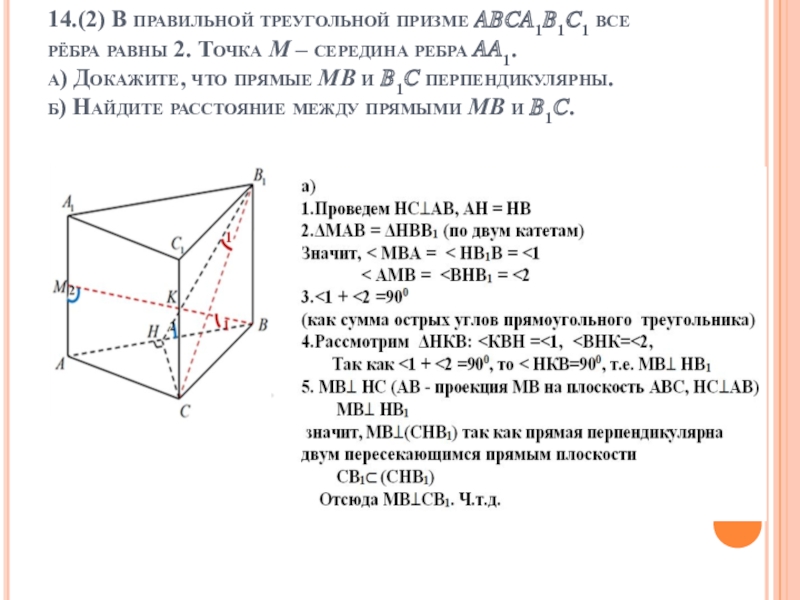
- 8. 14.(2) В правильной треугольной призме ????1?1?1 все
- 9. 14.(2) В правильной треугольной призме ????1?1?1 все
- 10. 14.(2) В правильной треугольной призме ????1?1?1 все
- 11. 14.(2) В правильной треугольной призме ????1?1?1 все
- 12. 14.(3) В правильной треугольной призме ????1?1?1 все
- 13. 14.(3) В правильной треугольной призме ????1?1?1 все
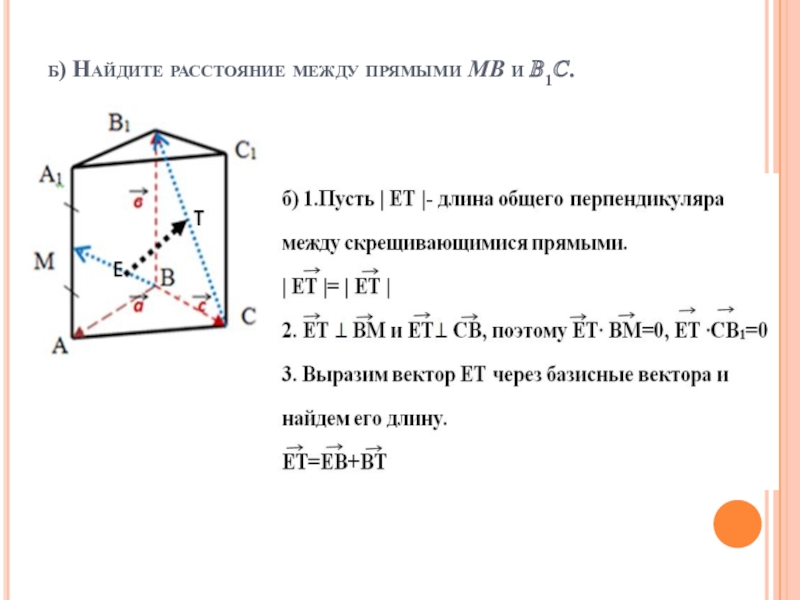
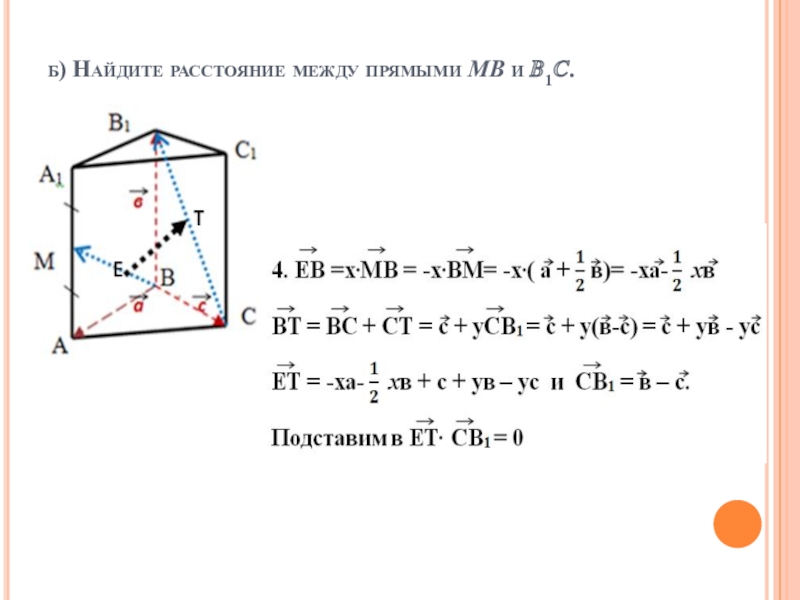
- 14. б) Найдите расстояние между прямыми MB и ?1?.
- 15. б) Найдите расстояние между прямыми MB и ?1?.
- 16. б) Найдите расстояние между прямыми MB и ?1?.
- 17. б) Найдите расстояние между прямыми MB и ?1?.
- 18. б) Найдите расстояние между прямыми MB и ?1?.
- 19. б) Найдите расстояние между прямыми MB и ?1?.
- 20. Источники.Решу ЕГЭ https://ege.sdamgia.ru/
Слайд 1Три способа решения одной задачи. Математика. Профиль. С№14
Подготовила Кисленкова Татьяна Ивановна,
учитель
2018
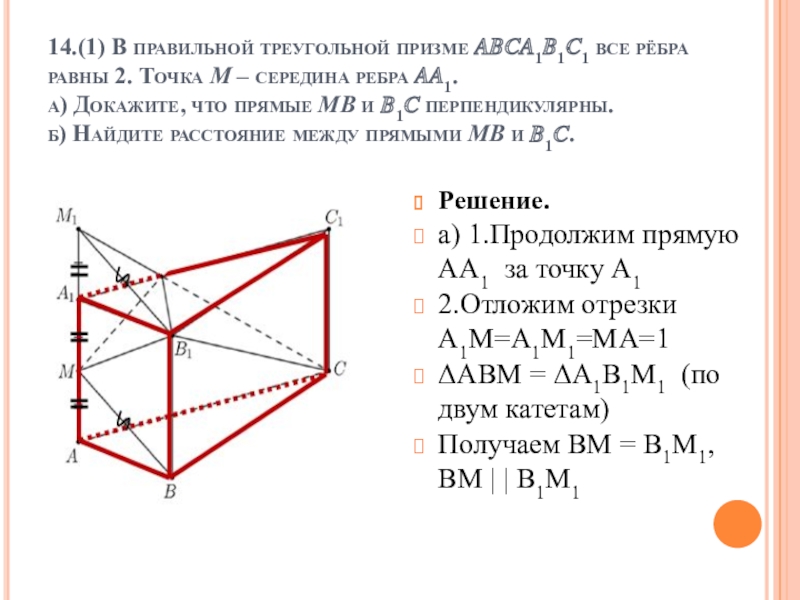
Слайд 214.(1) В правильной треугольной призме ????1?1?1 все рёбра равны 2. Точка
Решение.
а) 1.Продолжим прямую АА1 за точку А1
2.Отложим отрезки А1М=А1М1=МА=1
ΔАВМ = ΔА1В1М1 (по двум катетам)
Получаем ВМ = В1М1, ВМ | | В1М1
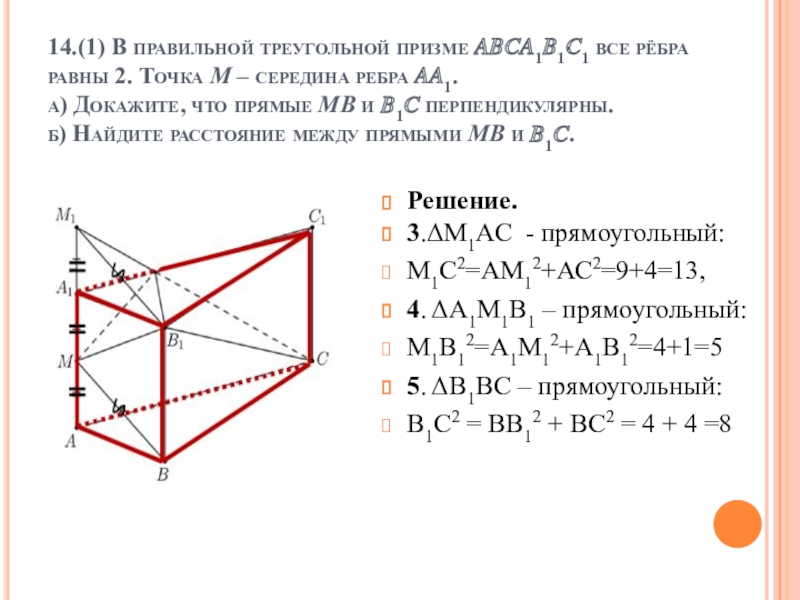
Слайд 314.(1) В правильной треугольной призме ????1?1?1 все рёбра равны 2. Точка
Решение.
3.ΔМ1АС - прямоугольный:
М1С2=АМ12+АС2=9+4=13,
4. ΔА1М1В1 – прямоугольный:
М1В12=А1М12+А1В12=4+1=5
5. ΔВ1ВС – прямоугольный:
В1С2 = ВВ12 + ВС2 = 4 + 4 =8
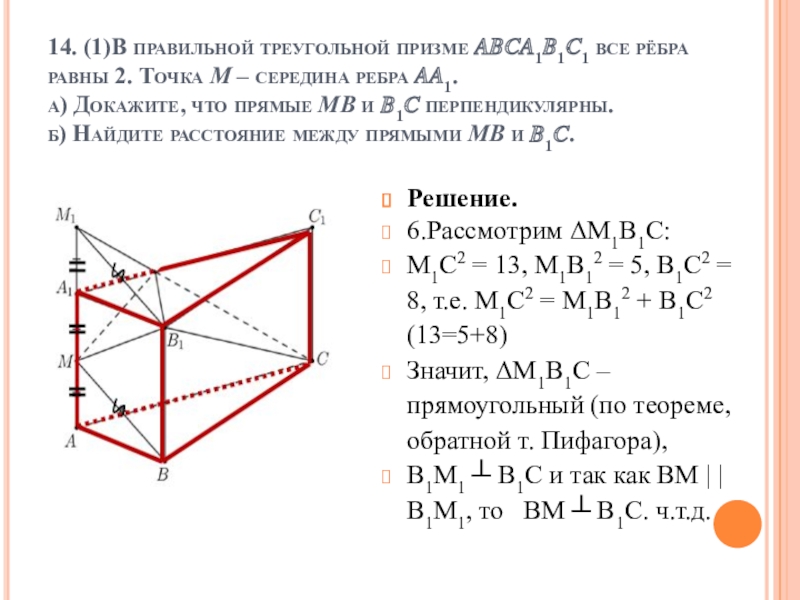
Слайд 414. (1)В правильной треугольной призме ????1?1?1 все рёбра равны 2. Точка
Решение.
6.Рассмотрим ΔМ1В1С:
М1С2 = 13, М1В12 = 5, В1С2 = 8, т.е. М1С2 = М1В12 + В1С2 (13=5+8)
Значит, ΔМ1В1С – прямоугольный (по теореме, обратной т. Пифагора),
В1М1 ┴ В1С и так как ВМ | | В1М1, то ВМ ┴ В1С. ч.т.д.
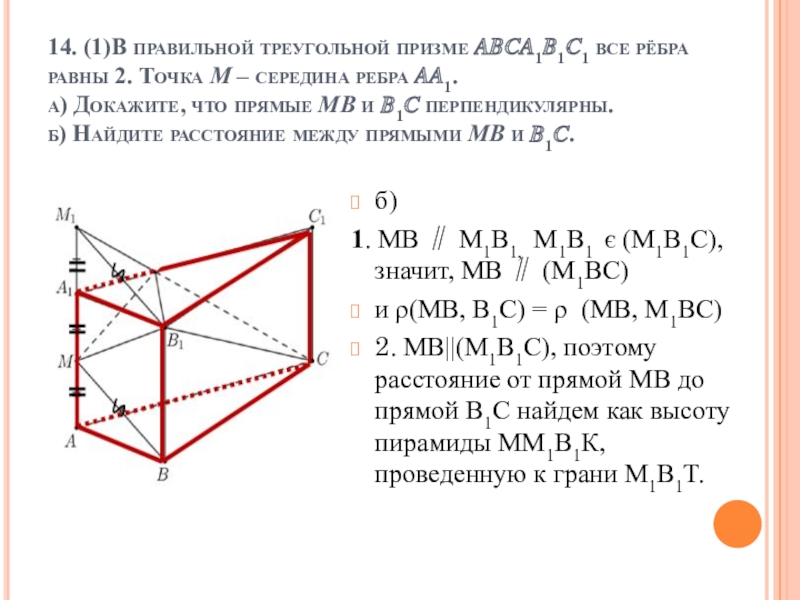
Слайд 514. (1)В правильной треугольной призме ????1?1?1 все рёбра равны 2. Точка
б)
1. МВ ∥ М1В1, М1В1 є (М1В1С), значит, МВ ∥ (М1ВС)
и ρ(МВ, В1С) = ρ (МВ, М1ВС)
2. МВ||(М1В1С), поэтому расстояние от прямой МВ до прямой В1С найдем как высоту пирамиды ММ1В1К, проведенную к грани М1В1Т.