Иошина Светлана Викторовна – учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Теорема Виета (8 класс)
Содержание
- 1. Презентация по математике Теорема Виета (8 класс)
- 2. "Хоть выйди ты не в белый свет,
- 3. Неполные кв. уравнениеax2 +bx =0, ax2 +c =0 Квадратное уравнениеКоличество корней: 0,1,2Приведенное квадратное уравнениеа=0 D
- 4. Цели урока 1. Как связаны коэффициенты приведенного
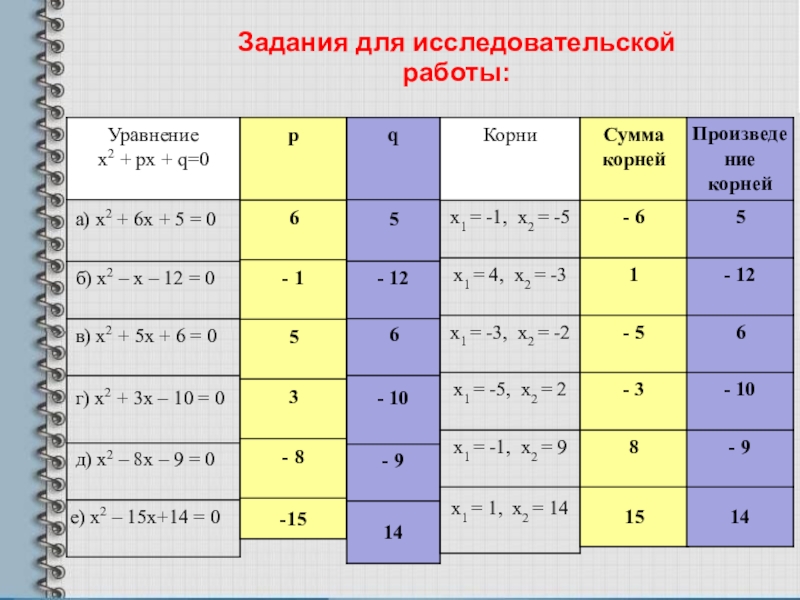
- 5. Задания для исследовательской работы:
- 6. Слайд 6
- 7. Теорема Виета:Знаменитая теорема, устанавливающая связь коэффициентов приведенного
- 8. Француз, жил в конце XVI - начале
- 9. Слайд 9
- 10. Для чего нужна теорема Виета?1. Находить подбором
- 11. Устная работа
- 12. Слайд 12
- 13. а) х2 – 15х – 16 =
- 14. Составьте квадратное уравнение3 и 5х2 – 8х
- 15. Составьте квадратное уравнение. -3 и 5
- 16. Составьте квадратное уравнение.3 и -5 Х2+2х-15=0х2 +
- 17. Составьте квадратное уравнение.-3 и –5z2+ 8z +
- 18. СР. Теорема ВиетаВариант А1Для уравнения, имеющего корни
- 19.
- 20. Рефлексия1. Сегодня на уроке я узнал(а)…2. Было
- 21. Домашнее задание п.23, №329 (2), 330 (2),
- 22. Спасибо за урок!
- 23. План исследованияЗаполните рабочий лист. Сравните результаты колонок
Слайд 2"Хоть выйди ты не в белый свет, А в поле за околицей,
Н. Рыленков
(1909—1969)
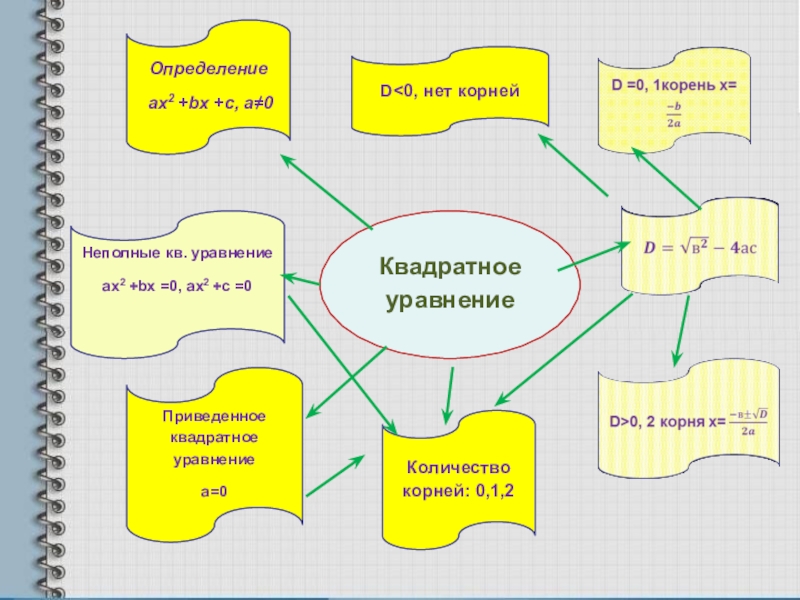
Слайд 3Неполные кв. уравнение
ax2 +bx =0, ax2 +c =0
Квадратное уравнение
Количество корней: 0,1,2
Приведенное
а=0
D<0, нет корней
Определение
ах2 +bx +c, a≠0
Слайд 4Цели урока
1. Как связаны коэффициенты приведенного квадратного уравнения и его корни.
2.
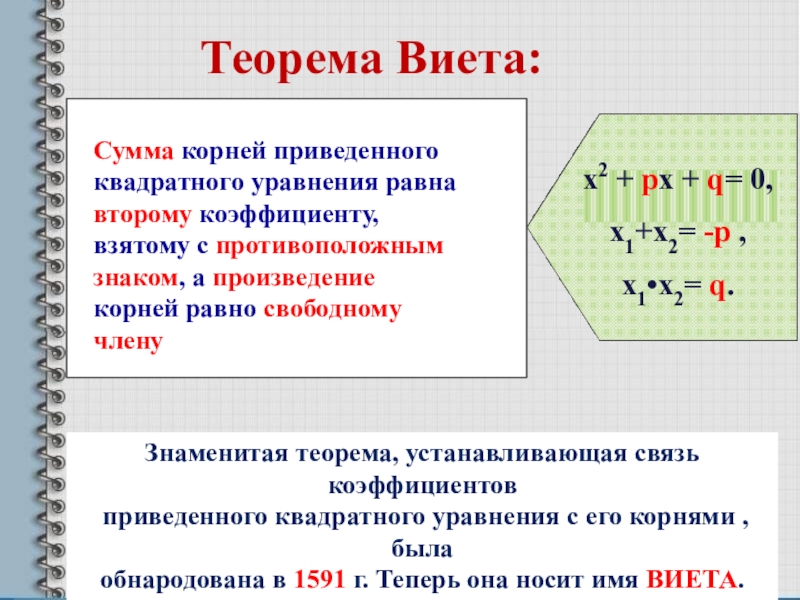
Слайд 7Теорема Виета:
Знаменитая теорема, устанавливающая связь коэффициентов
приведенного квадратного уравнения с его
обнародована в 1591 г. Теперь она носит имя ВИЕТА.
х2 + рх + q= 0,
х1+х2= -р ,
х1•х2= q.
Слайд 8Француз, жил в конце XVI - начале XVII веков, по профессии
Франсуа Виет
(1540 – 1603)
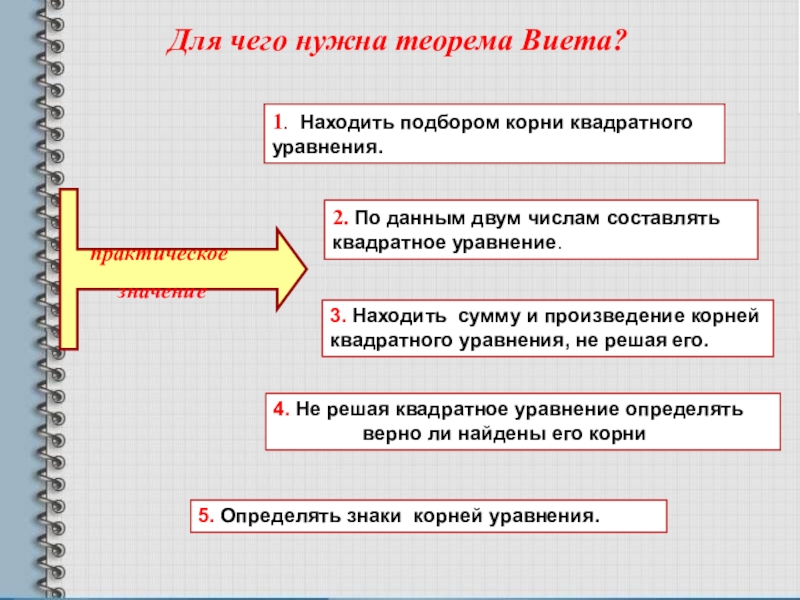
Слайд 10Для чего нужна теорема Виета?
1. Находить подбором корни квадратного уравнения.
2. По
3. Находить сумму и произведение корней квадратного уравнения, не решая его.
4. Не решая квадратное уравнение определять
верно ли найдены его корни
5. Определять знаки корней уравнения.
Слайд 12 1) х2 – 37х
Найдите сумму и произведение корней квадратных уравнений
х2 + px + q = 0
x1 + x2 = - p
x1 • x2 = q
Слайд 13а) х2 – 15х – 16 = 0
х1 = - 1; х2 = 16. х1 = 7; х2 = -4.
г) х2 + 12х + 20 = 0,
х1 = - 2; х2 = -10 х1 = 1; х2 = 8
2. Проверьте с помощью теоремы Виета: верно ли найдены корни квадратного уравнения.
в) х2 - 9х + 8 = 0,
х2 + px + q = 0
x1 + x2 = - p
x1 • x2 = q
Слайд 17Составьте квадратное уравнение.
-3 и –5
z2+ 8z + 15 = 0
х2 +
x1 + x2 = - p
x1 • x2 = q
Слайд 18СР. Теорема Виета
Вариант А1
Для уравнения, имеющего корни х1 и х2, найдите
а) х² - 3х -10 = 0, б) х² +10х +21 = 0,
х1 + х2 = 3, х1 + х2 = -10,
х1 ∙ х2 =- 10. х1 ∙ х2 = 21.
2. Найти подбором корни уравнения
х² - 8х + 15 = 0. Выберите верный ответ.
А. 5 и -3; Б. 5 и 3; В. -5 и -3; Г. -5 и 3.
3. Составьте квадратное уравнение, имеющее корни 10 и -3.
х1 + х2 = - 7
х1 ∙ х2 = - 30
х² +7х – 30 = 0
Слайд 20Рефлексия
1. Сегодня на уроке я узнал(а)…
2. Было интересно…
3. Было трудно…
4. Я
5. Я понял(а), что…
6. Теперь я могу…
7. Я почувствовал(а), что…
8. Я приобрел(а)…
9. Я научился(ась)…
Слайд 21Домашнее задание
п.23, №329 (2), 330 (2), 332 (1,4), 333 (2,4).
Творческое задание:
Доказать, что если в квадратном уравнении
ах2+bx+c=0:
1) а + b + c = 0, то х1= 1, х2 =
Слайд 23План исследования
Заполните рабочий лист.
Сравните результаты колонок №2 и №5 по
Сравните результаты колонок №3 и №6 по каждому уравнению, найдите закономерность между коэффициентами и корнями, сделайте вывод.