- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Теорема Пика
Содержание
- 1. Презентация по математике Теорема Пика
- 2. Георг Александр Пик (10 августа 1859 – 13
- 3. Формула Пика В вариантах ЕГЭ присутствует целая
- 4. Доказательство теоремы Пика Сначала заметим, что формула
- 5. Остается сделать последний шаг: перейти от
- 6. Рассмотрим пример. 1. Возьмём многоугольник без специальной
- 7. Источникиhttps://matematikalegko.ru/formuli/ploshhad-figury-na-liste-v-kletku-formula-pika.htmlhttp://hijos.ru/2011/09/14/formula-pika/https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9F%D0%B8%D0%BA%D0%B0https://ru.wikipedia.org/wiki/%D0%9F%D0%B8%D0%BA,_%D0%93%D0%B5%D0%BE%D1%80%D0%B3
Слайд 1Теорема Пика
Использование формулы Пика для нахождения площади многоугольников
Подготовила: учитель математики
ГБОУ «Шебекинская
Клевцова С.В.
Слайд 2Георг Александр Пик
(10 августа 1859 – 13 июля 1942)
Учёба
Георга, который
Работы
Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифференциальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца — Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.
Слайд 3Формула Пика
В вариантах ЕГЭ присутствует целая группа заданий, в
Площади типовых многоугольников, таких как параллелепипед, трапеция и треугольник, легко найти через соответствующие формулы площадей фигур. Но что делать, если у представленной фигуры нет специальной формулы нахождения площади? В таком случае уместно использование формулы Пика для нахождения площади многоугольника.
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
Формула Пика
Слайд 4Доказательство теоремы Пика
Сначала заметим, что формула Пика верна для единичного
Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b . Имеем в этом случае
и, по формуле Пика,
Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек.
Тогда для этого случая
и получаем, что
Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (см. рисунки). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.
Слайд 5
Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой
Пусть многоугольник M и треугольник T имеют общую сторону. Предположим, что для M формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из M добавлением T. Так как M и T имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через и получим
— число внутренних целочисленных точек нового многоугольника,
— число граничных точек нового многоугольника.
Из этих равенств получаем
Так как мы предположили, что теорема верна для M и для T по отдельности, то
Тем самым, формула Пика доказана.
Теорема Пика доказана.
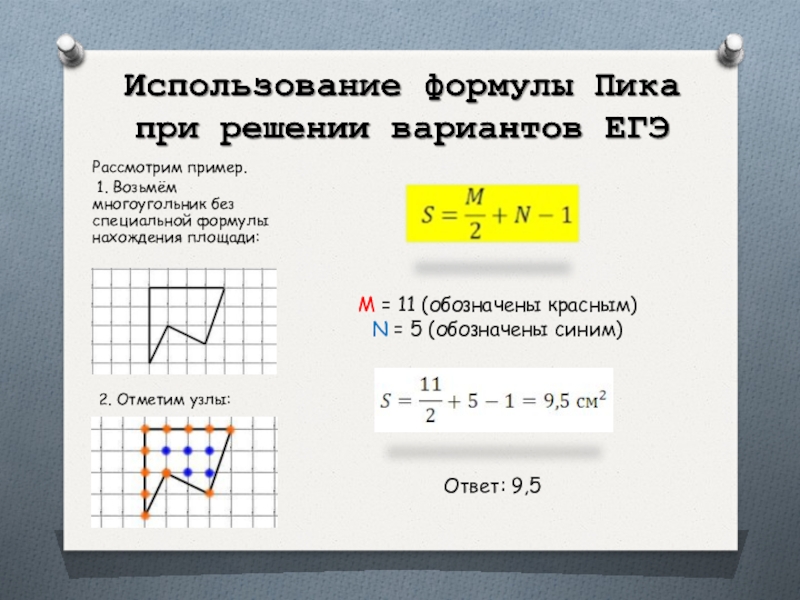
Слайд 6Рассмотрим пример.
1. Возьмём многоугольник без специальной формулы нахождения площади:
2. Отметим
M = 11 (обозначены красным)
N = 5 (обозначены синим)
Ответ: 9,5