- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Прямые линии в Декартовой системе координат, 11 класс
Содержание
- 1. Презентация по математике Прямые линии в Декартовой системе координат, 11 класс
- 2. and y-intercept, c = The equation of a straight line is
- 3. The coordinates of any point lying on
- 4. Finding the equation of a straight line
- 5. If we don’t know the gradient, we
- 6. 42e.g.
- 7. Слайд 7
- 8. Слайд 8
- 9. The gradient of the straight line joining
- 10. To find the equation of a straight
- 11. SUMMARYEquation of a straight lineGradient of a
- 12. 2. Find the equation of the line through the points ExerciseSolution: So,Solution: So,
- 13. We sometimes rearrange the equation of a
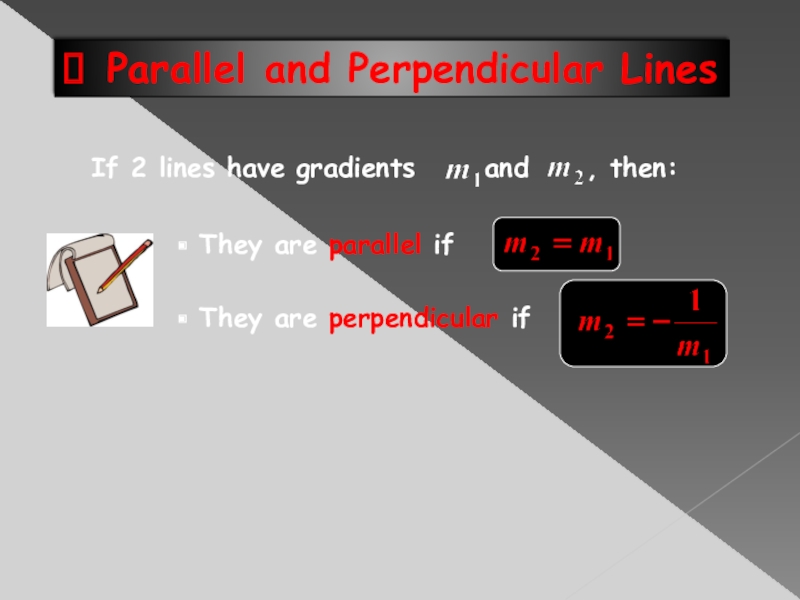
- 14. Parallel and Perpendicular Lines
- 15. Слайд 15
- 16. We don’t usually leave fractions ( or decimals ) in equations. So, multiplying by 2:
- 17. If the gradient isn’t given, find the
- 18. Solution: So,Solution: So,Parallel line isSo,
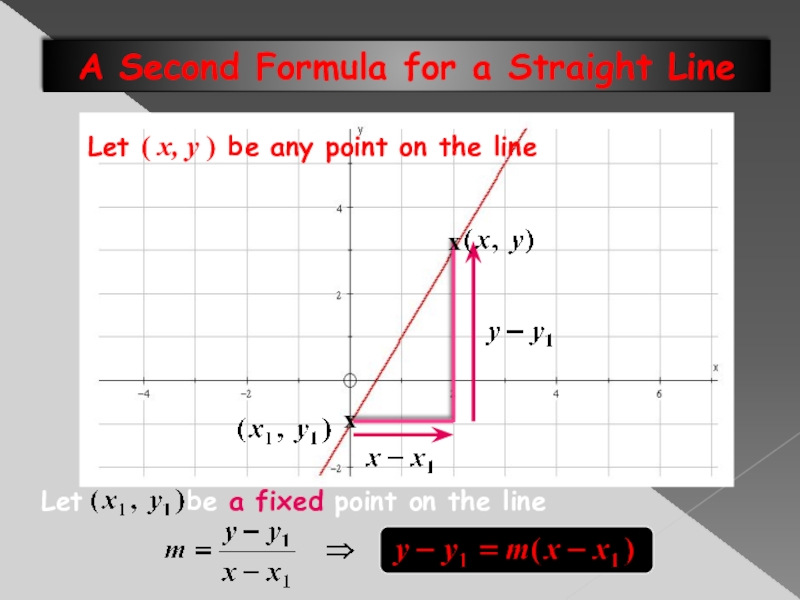
- 19. A Second Formula for a Straight LineLet
- 20. Solution: First find the gradientWe could use the 2nd point,(-1, 3) instead of (2, -3)
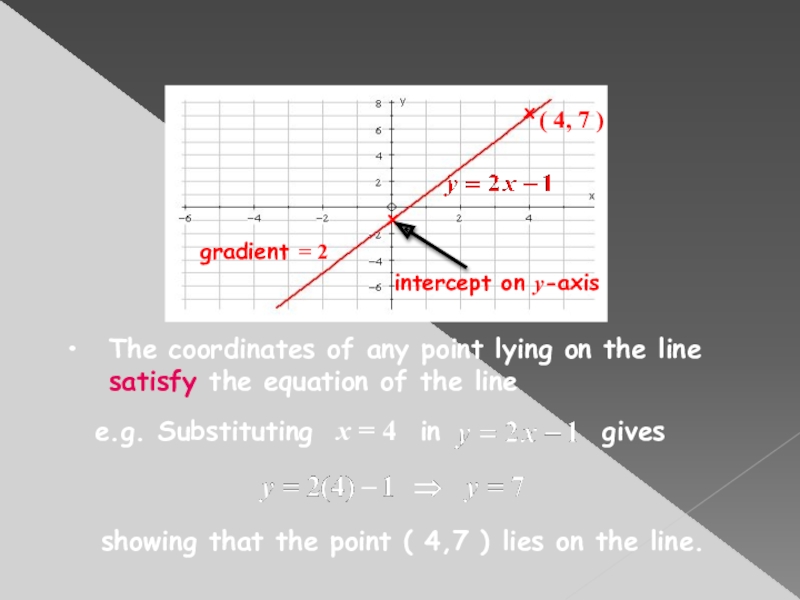
Слайд 3The coordinates of any point lying on the line satisfy the
showing that the point ( 4,7 ) lies on the line.
Слайд 4Finding the equation of a straight line when we know
its gradient,
the coordinates of a point on the line.
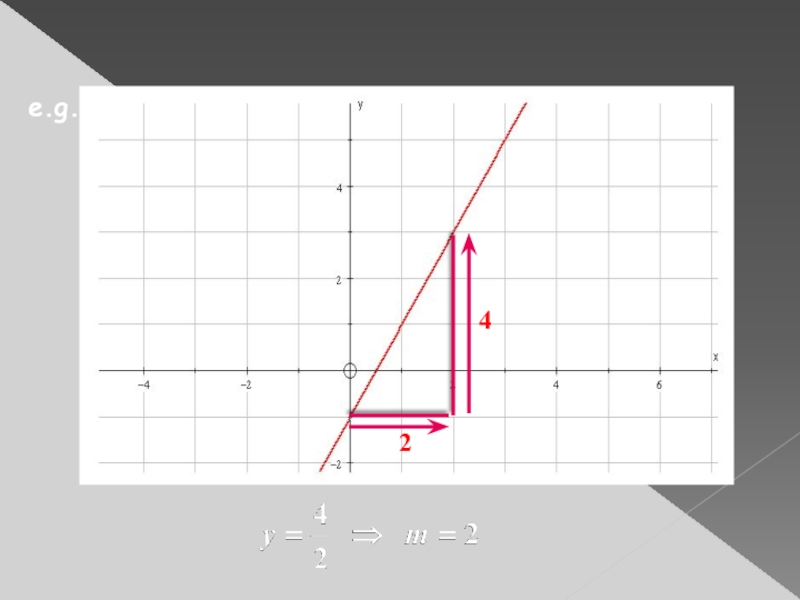
Слайд 5If we don’t know the gradient, we have to find it
We develop the formula by reminding ourselves about the meaning of a gradient.
To do this, we can use a formula.
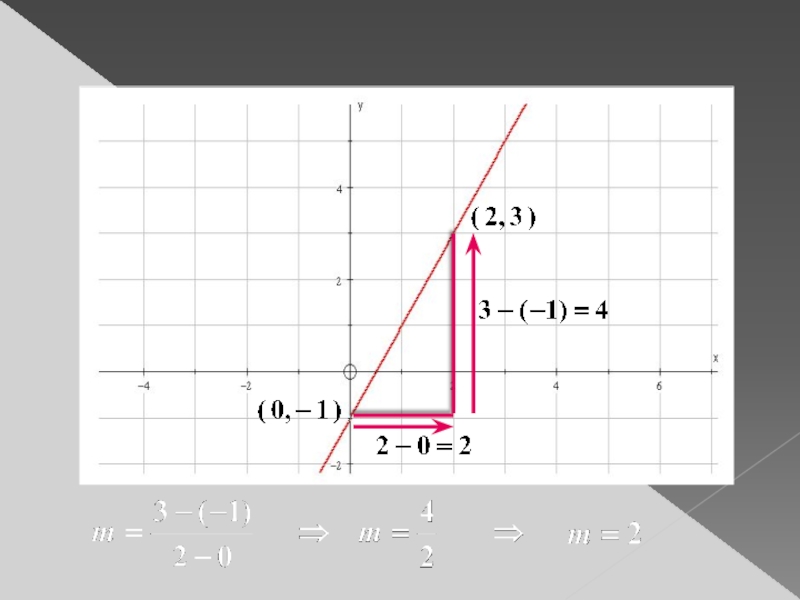
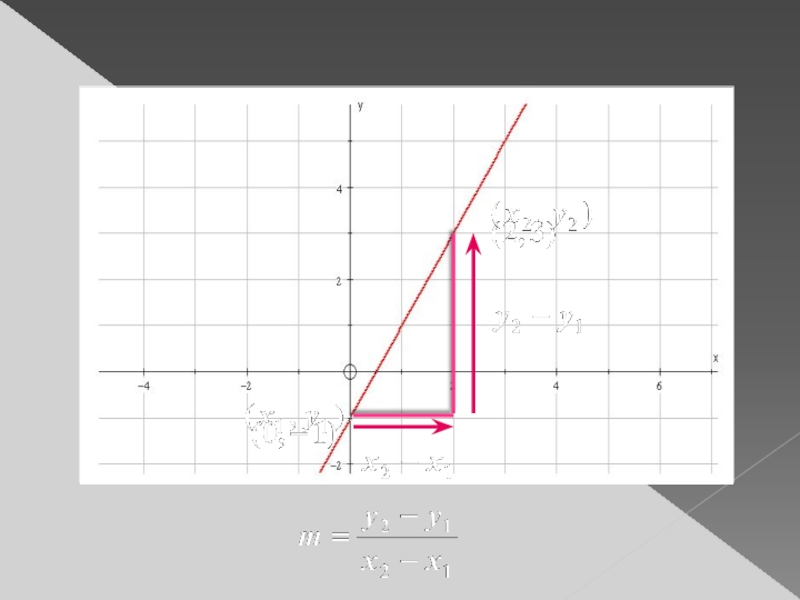
Слайд 9The gradient of the straight line joining the points
and
is
To use this
Solution:
Слайд 10To find the equation of a straight line given 2 points
Solution: First find the gradient:
Слайд 11SUMMARY
Equation of a straight line
Gradient of a straight line
where m is
Слайд 13We sometimes rearrange the equation of a straight line so that
We must take care with the equation in this form.
Слайд 17If the gradient isn’t given, find the gradient using
Method of finding
SUMMARY