- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Простые числа
Содержание
- 1. Презентация по математике Простые числа
- 2. Вопрос : Как же используются простые числа
- 3. ПРОСТЫЕ ЧИСЛАПростое число - натуральное число,
- 4. Решето ЭратосфенаАлгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому.
- 5. ПРОСТЫЕ ЧИСЛА В НАУКЕДело в том,
- 6. Что такое криптография ?Криптография — наука о методах
- 7. Абу Юсуф Якуб ибн Исхак ибн Сабах
- 8. Разновидности криптографии. 1. Разложение больших чисел на простые
- 9. 2. Вычисление дискретного логарифма или дискретное возведение в степень(алгоритм Диффи-Хелмана-Меркла).
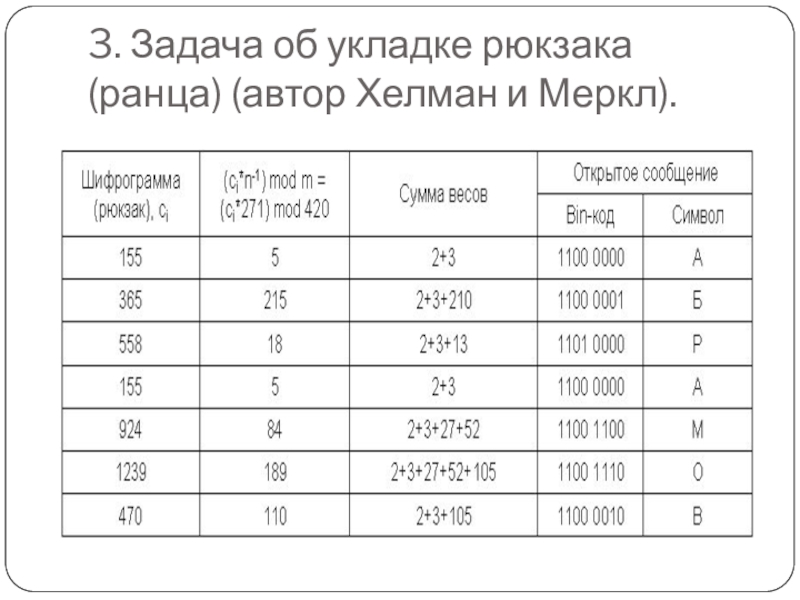
- 10. 3. Задача об укладке рюкзака (ранца) (автор Хелман и Меркл).
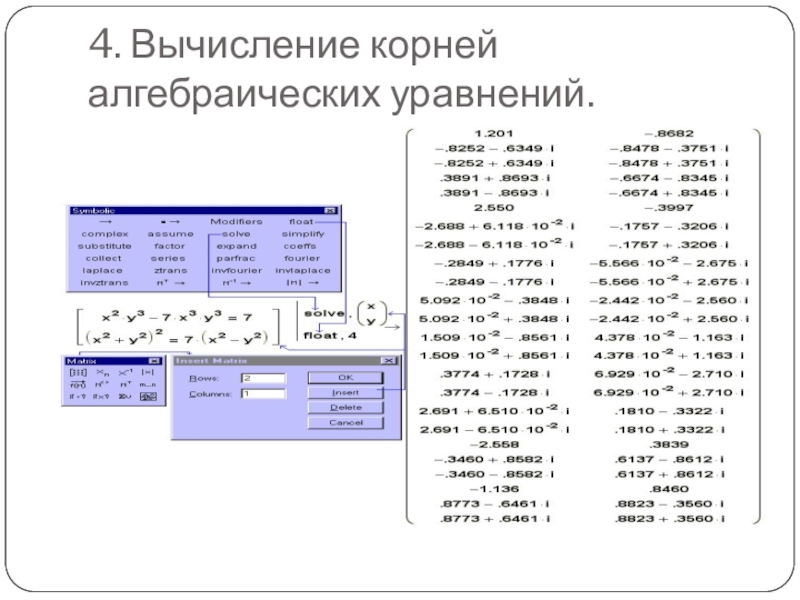
- 11. 4. Вычисление корней алгебраических уравнений.
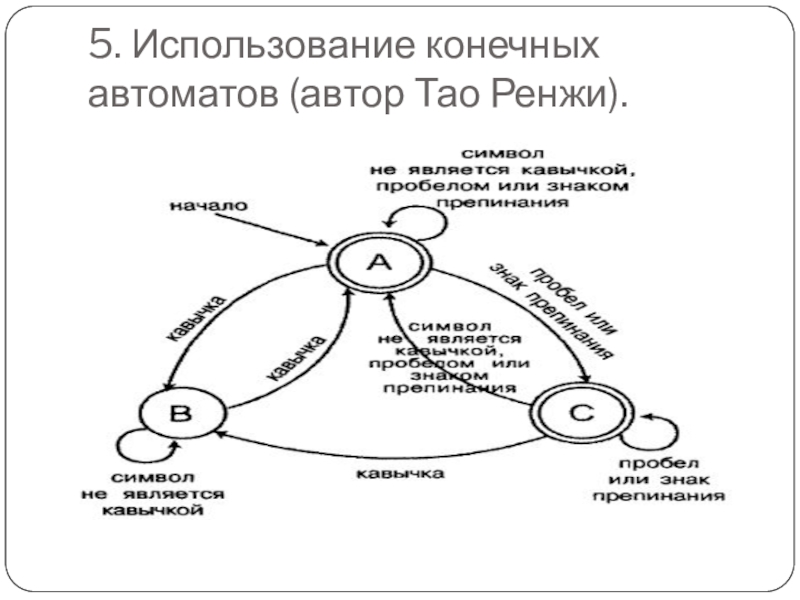
- 12. 5. Использование конечных автоматов (автор Тао Ренжи).
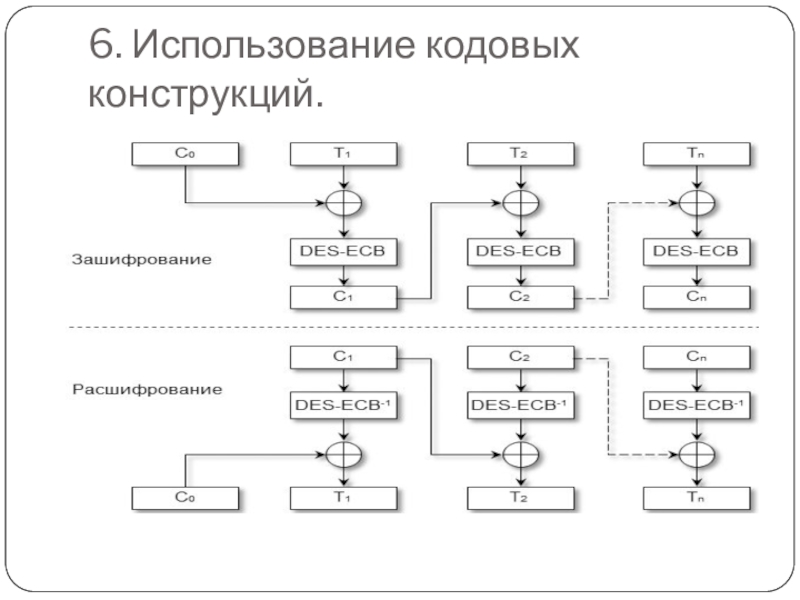
- 13. 6. Использование кодовых конструкций.
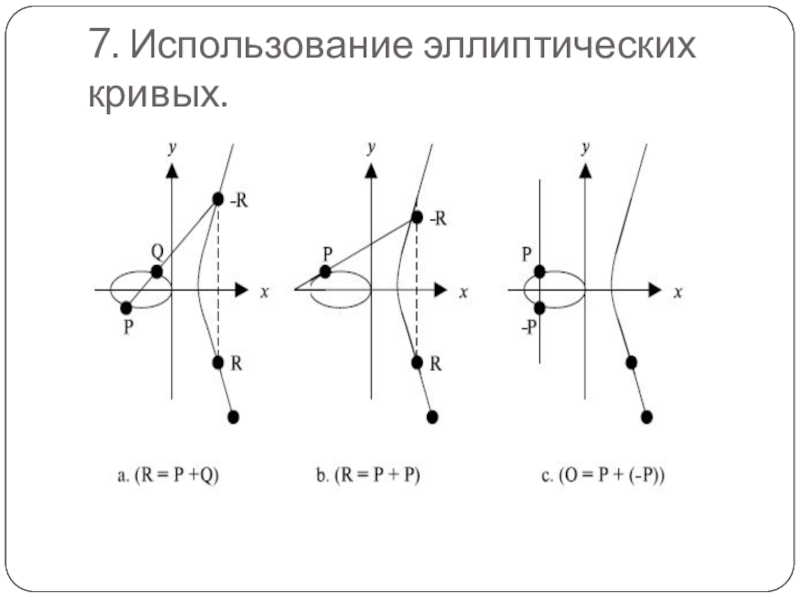
- 14. 7. Использование эллиптических кривых.
- 15. Рассмотрим RSA. Стойкость RSA основывается на большой
- 16. Свой шифр. Любой полноценный код требует наличия книги
- 17. Трудно ли писать текст этим шифром?С
- 18. А также замерить время в настоящей жизни
- 19. Если же текст нужен для дешифровки ,то
- 20. Сравнив результаты, я понял, что с помощью
- 21. Вывод.В своей работе я изучил криптографию и
- 22. СПАСИБО ЗА ВНИМАНИЕ !
Вопрос : Как же используются простые числа в других науках ?Предмет исследования: простые числа . Объект исследования : множество простых чисел, наука -криптография .Цель: Изучить историю простых чисел до настоящего времени и их значимость в криптографии
Слайд 2Вопрос : Как же используются простые числа в других науках ?
Предмет
исследования: простые числа .
Объект исследования : множество простых чисел, наука -криптография .
Цель: Изучить историю простых чисел до настоящего времени и их значимость в криптографии , создать свой необычный шифр .
Задачи :
1. Рассказать о простых числах и их истории.
2.Ввести понятие криптография.
3.Познакомиться с шрифтами криптографии .
4.Попробовать использовать свой шифр .
Актуальность на сегодняшний день :
Актуальна ? Да! Так как сейчас век коммуникационных технологий и шифрование стало интересно для всех потребителей т.к. необходимо защищать свои данные находящиеся в негосударственных каналах связи.
Объект исследования : множество простых чисел, наука -криптография .
Цель: Изучить историю простых чисел до настоящего времени и их значимость в криптографии , создать свой необычный шифр .
Задачи :
1. Рассказать о простых числах и их истории.
2.Ввести понятие криптография.
3.Познакомиться с шрифтами криптографии .
4.Попробовать использовать свой шифр .
Актуальность на сегодняшний день :
Актуальна ? Да! Так как сейчас век коммуникационных технологий и шифрование стало интересно для всех потребителей т.к. необходимо защищать свои данные находящиеся в негосударственных каналах связи.
Слайд 3 ПРОСТЫЕ ЧИСЛА
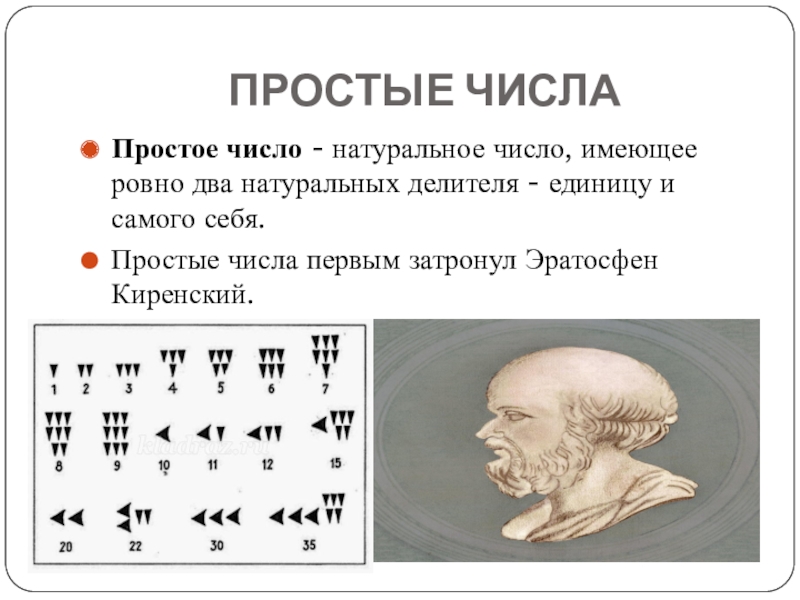
Простое число - натуральное число, имеющее ровно два натуральных
делителя - единицу и самого себя.
Простые числа первым затронул Эратосфен Киренский.
Простые числа первым затронул Эратосфен Киренский.
Слайд 4Решето Эратосфена
Алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену
Киренскому.
Слайд 5 ПРОСТЫЕ ЧИСЛА В НАУКЕ
Дело в том, что простые числа лежат
в основе систем шифрования, широко используемых в сети.
Слайд 6Что такое криптография ?
Криптография — наука о методах обеспечения конфиденциальности (невозможности прочтения
информации посторонним) и аутентичности (целостности и подлинности авторства, а также невозможности отказа от авторства) информации посредством шифрования данных.
Криптография является одной из двух частей (вторая часть - криптоанализ) большой науки криптологии.
1. Преобразование исходного текста должно быть условно необратимым и исключать его восстановление на основе открытого ключа.
2. Определение закрытого ключа на основе открытого также должно быть невозможным на современном технологическом уровне.
Все предлагаемые сегодня криптосистемы с открытым ключом опираются на один из следующих типов односторонних преобразований
Криптография является одной из двух частей (вторая часть - криптоанализ) большой науки криптологии.
1. Преобразование исходного текста должно быть условно необратимым и исключать его восстановление на основе открытого ключа.
2. Определение закрытого ключа на основе открытого также должно быть невозможным на современном технологическом уровне.
Все предлагаемые сегодня криптосистемы с открытым ключом опираются на один из следующих типов односторонних преобразований
Слайд 7Абу Юсуф Якуб ибн Исхак ибн Сабах аль-Кинди
Он написал почти
300 трудов по теории математики, медицины, лингвистики, астрологии и музыки. Его знаменитая книга о расшифровке криптографического сообщения была обнаружена только в 1987-м в стамбульских архивах.
Слайд 8Разновидности криптографии.
1. Разложение больших чисел на простые множители (алгоритм RSA).
1
Выбираются два простых
числа p и q.
p=7, q=13
2
Вычисляется произведение n = p * q.
n=91
3
Вычисляется функция Эйлера2 φ(n).
φ(n) = (7-1)(13-1) = 91-7-13+1 = 72
4
Выбирается открытый ключ e, как произвольное число (0 < e < n), взаимно простое3 с результатом функции Эйлера (e ⊥ φ(n)).
e=5
5
Вычисляется закрытый ключ d, как обратное число к e по модулю φ(n), из соотношения (d*e) mod φ(n) = 1.
(d*5) mod 72 = 1, d = 29
6
Публикуются открытый ключ (e, n) в специальном хранилище, где исключается возможность его подмены (общедоступном сертифицированном справочнике).
p=7, q=13
2
Вычисляется произведение n = p * q.
n=91
3
Вычисляется функция Эйлера2 φ(n).
φ(n) = (7-1)(13-1) = 91-7-13+1 = 72
4
Выбирается открытый ключ e, как произвольное число (0 < e < n), взаимно простое3 с результатом функции Эйлера (e ⊥ φ(n)).
e=5
5
Вычисляется закрытый ключ d, как обратное число к e по модулю φ(n), из соотношения (d*e) mod φ(n) = 1.
(d*5) mod 72 = 1, d = 29
6
Публикуются открытый ключ (e, n) в специальном хранилище, где исключается возможность его подмены (общедоступном сертифицированном справочнике).
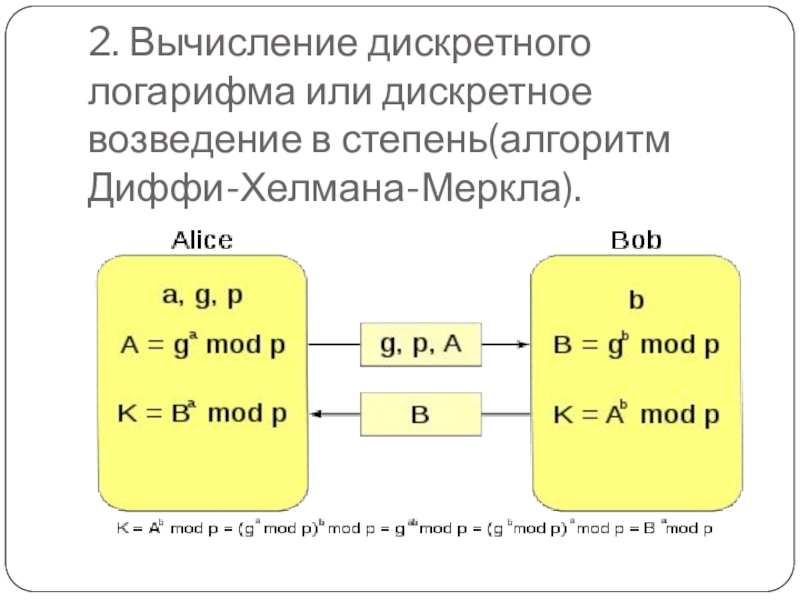
Слайд 92. Вычисление дискретного логарифма или дискретное возведение в степень(алгоритм Диффи-Хелмана-Меркла).
Слайд 15Рассмотрим RSA.
Стойкость RSA основывается на большой вычислительной сложности известных алгоритмов разложения
числа на простые сомножители (делители). Например, легко найти произведение двух простых чисел 7 и 13 даже в уме – 91. Попробуйте в уме найти два простых числа, произведение которых равно 323 (числа 17 и 19). Конечно, для современной вычислительной техники найти дв а простых числа, произведение которых равно 323, не проблема. Поэтому для надежного шифрования алгоритмом RSA, как правило, выбираются простые числа, количество двоичных разрядов которых равно нескольким сотням.
Слайд 16Свой шифр.
Любой полноценный код требует наличия книги кода.
Я придумал цифры, замещающие
необходимые нам буквы, затем собрал их всех вместе в книге кода, чтобы вы могли прочитать мое послание .
Слайд 17 Трудно ли писать текст этим шифром?
С помощью системы Паскаль решил
вычислить примерное время для написания текста в 100 слов , с помощью моего шифра .Примерное время -25 минут .Эту программу мы в данный момент изучаем по ИКТ .
Слайд 18А также замерить время в настоящей жизни с помощью секундомера .Время
написания -28,47.45. Написанный текст не используется для дешифрования он был написан исключительно для замера времени .
Слайд 19Если же текст нужен для дешифровки ,то мы действуем по принципу
"основа "Этот принцип заключается в том , чтобы после каждой зашифрованной буквы ставить току ,а слово каждое отдельное слово брать в "основу ".
Слайд 20Сравнив результаты, я понял, что с помощью программы Паскаль мы можем
делать расчеты удобно и быстро .
Слайд 21Вывод.
В своей работе я изучил криптографию и простые числа. При изучение
криптографических ключей понял ,что алгоритм RSA максимально тесно связан с простыми числами. Составил совой криптографический шифр. Простые числа стали неотъемлемой частью криптографических преобразований , а также ввели вас в мир написания и вскрытия шифров.