- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Приёмы быстрого счёта
Содержание
- 1. Презентация по математике Приёмы быстрого счёта
- 2. Иоганн Генрих Песталоцци«Счёт, вычисления – основа порядка в голове»
- 3. Устный счёт — математические вычисления, осуществляемые человеком без
- 4. Говорят, если хотите научиться плавать, вы должны
- 5. Эта картина называется
- 6. Яков Трахтенберг (17 июня 1888, Одесса, Российская империя).
- 7. Система быстрого счета по Трахтенбергу. Эта книга
- 8. Цели данной работы:Изучить некоторые приемы
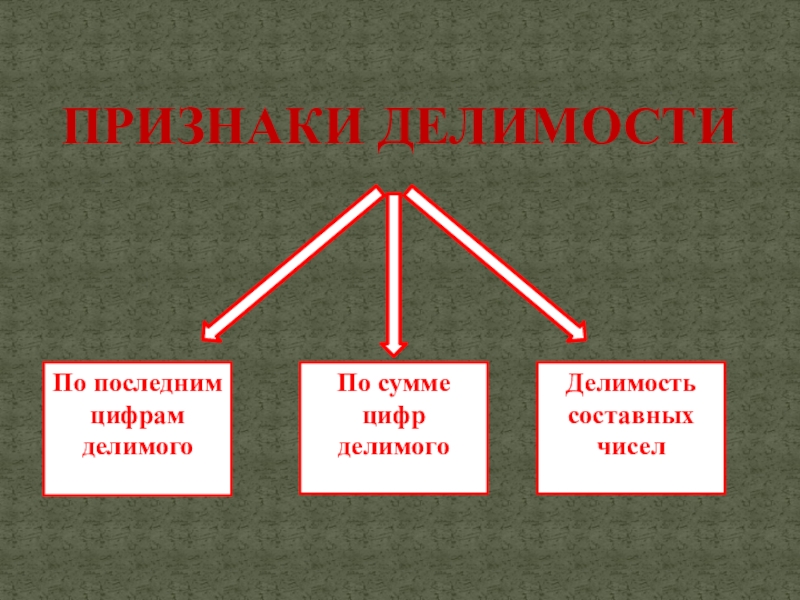
- 9. ПРИЗНАКИ ДЕЛИМОСТИ
- 10. Слайд 10
- 11. Слайд 11
- 12. 1. Признак делимости на 6. Число делится
- 13. 5. Признак делимости на 13. Число делится
- 14. Пиёмы быстрого деление и умножении чиселДеление на
- 15. Деление и умножение на 5. Чтобы любое
- 16. Умножение на 11.1 способ. Чтобы, умножить число
- 17. Умножение на 111, 1111, 11111 (для двузначных
- 18. Метод дополнения до 100 98
- 19. 462=(25-4)*100+42=2100+16=21164-дополнение до 50 532=(25+3)*100+32=28093-разница между 53 и 50 Метод дополнения до 50
- 20. Если запомнить
- 21. При возведении чисел в квадрат удобно используя
- 22. Чтобы возвести в квадрат число шестого десятка
- 23. Квадрат числа, оканчивающегося на 1
- 24. Квадрат числа, оканчивающегося на 9.
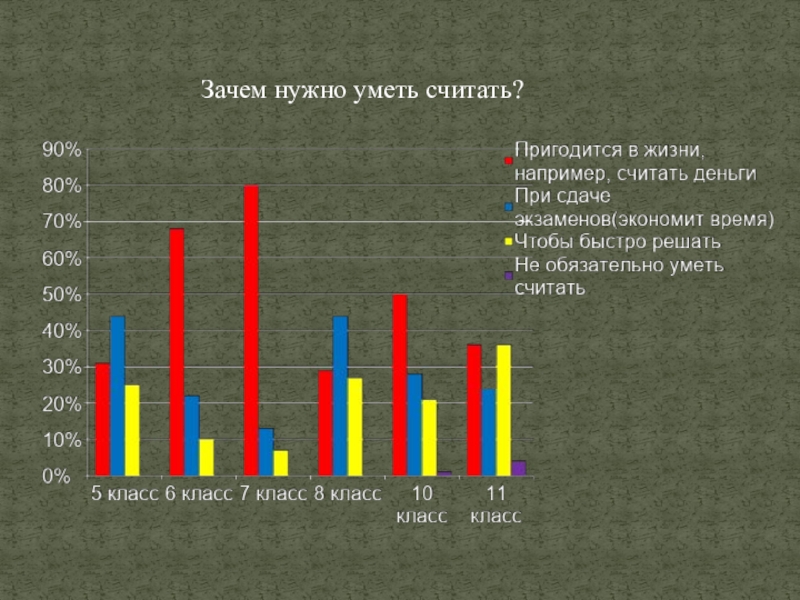
- 25. Зачем нужно уметь считать?
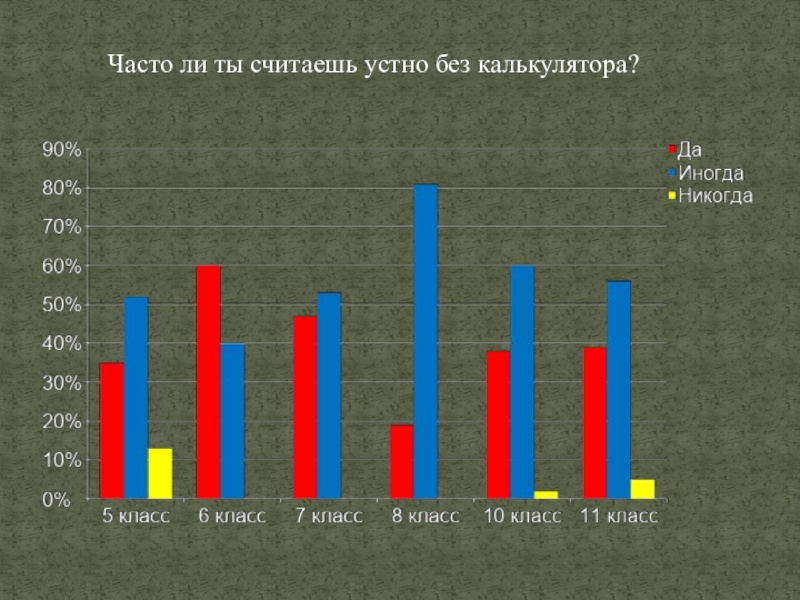
- 26. Часто ли ты считаешь устно без калькулятора?
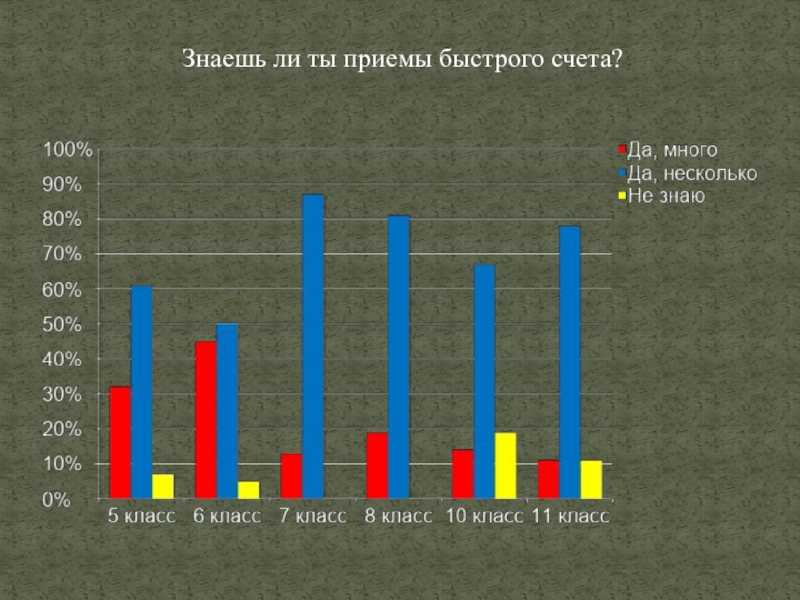
- 27. Знаешь ли ты приемы быстрого счета?
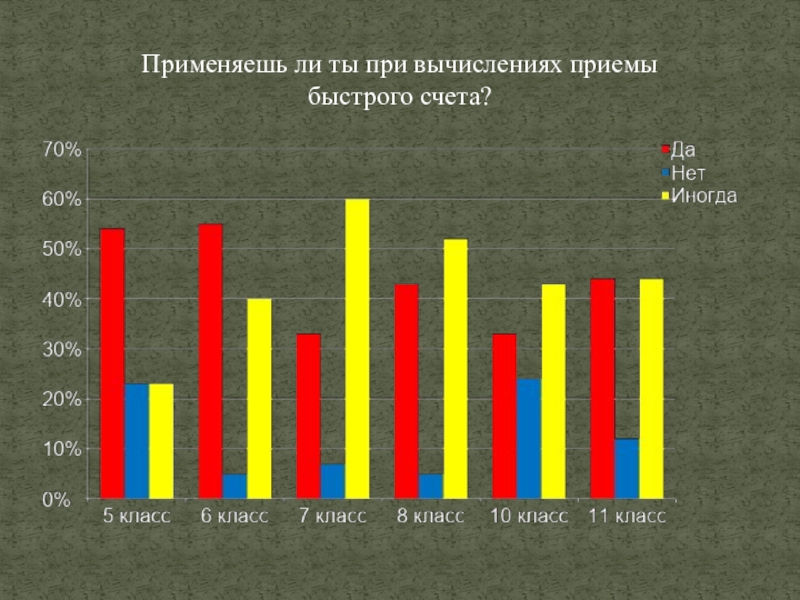
- 28. Применяешь ли ты при вычислениях приемы быстрого счета?
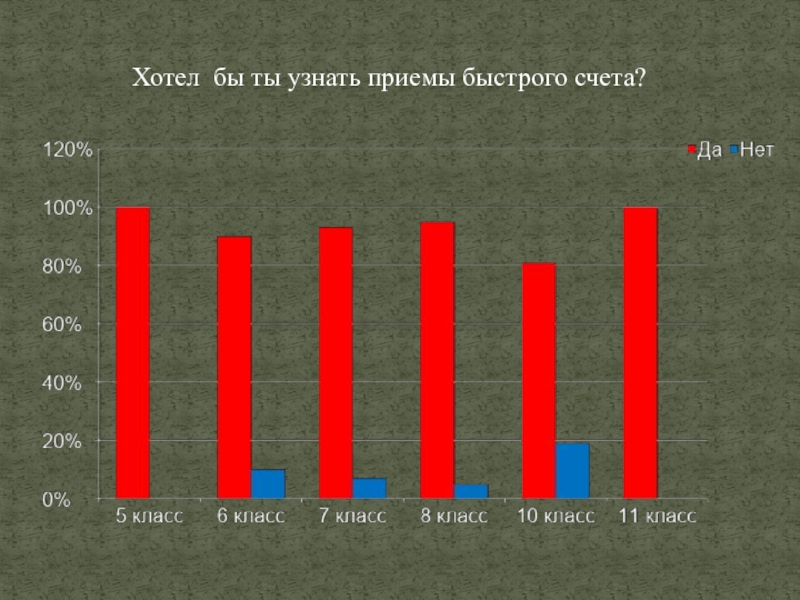
- 29. Хотел бы ты узнать приемы быстрого счета?
Иоганн Генрих Песталоцци«Счёт, вычисления – основа порядка в голове»
Слайд 3Устный счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер,
калькулятор, счеты и т. п.) и часто без приспособлений ( ручка, карандаш, бумага и т. п.).
Слайд 4Говорят, если хотите научиться плавать, вы должны войти в воду, а
если хотите уметь быстро считать , то должны начать считать.
Слайд 5 Эта картина называется «Устный счет». Написал ее художник Николай
Петрович Богданов – Бельский. 1895год. Художник изобразил на этой картине невыдуманных учеников и учителя, он очень хорошо знал своих героев: вырос в их среде. Учитель – это Сергей Александрович Рачинский, известный русский педагог, замечательный представитель русских образованных людей позапрошлого века.
Слайд 6Яков Трахтенберг (17 июня 1888, Одесса, Российская империя). Родился в Одессе, Российская
империя (сегодня Украина). Окончил с отличием Горный Институт в Петрограде, а позже работал на Адмиралтейских верфях в Обуховском заводе, где стал главным инженером, руководителем свыше 11 тысяч рабочих.
После Великой Октябрьской Революции 1917 года Трахтенберг перебрался в Германию. После прихода к власти Гитлера выступал против нацизма.
Во время Второй мировой войны. Трахтенберг стал узником нацистского концентрационного лагеря. В заключении разработал свою арифметическую систему, так называемый «Метод Трахтенберга».
После Великой Октябрьской Революции 1917 года Трахтенберг перебрался в Германию. После прихода к власти Гитлера выступал против нацизма.
Во время Второй мировой войны. Трахтенберг стал узником нацистского концентрационного лагеря. В заключении разработал свою арифметическую систему, так называемый «Метод Трахтенберга».
Слайд 7Система быстрого счета по Трахтенбергу. Эта книга представляет собой печатное изложение Э.
Катлером и Р. Мак-Шейном (Ann Cutler and Rudolph McShane) системы быстрого счета в уме, разработанной профессором, руководителем, а также и основателем Цюрихского Математического Института Яковом Трахтенбергом
Слайд 8
Цели данной работы:
Изучить некоторые приемы устного счета, позволяющие ускорить и оптимизировать
вычислительные процессы.
Развить память и математическую культуры мышления.
Развить творческие и интеллектуальные способности.
Продемонстрировать актуальность данной темы в наши дни. Научиться использовать данные приемы.
Задачи:
Воспользовавшись различными источниками информации собрать, изучить и систематизировать материал о приемах устного счета.
Рассмотреть некоторые приемы устного счета и на конкретных примерах показать преимущества их использования.
Провести микроисследование: «Наличие навыков устного счета залог успешной сдачи экзамена».
Развить память и математическую культуры мышления.
Развить творческие и интеллектуальные способности.
Продемонстрировать актуальность данной темы в наши дни. Научиться использовать данные приемы.
Задачи:
Воспользовавшись различными источниками информации собрать, изучить и систематизировать материал о приемах устного счета.
Рассмотреть некоторые приемы устного счета и на конкретных примерах показать преимущества их использования.
Провести микроисследование: «Наличие навыков устного счета залог успешной сдачи экзамена».
Слайд 12
1. Признак делимости на 6. Число делится на 6, если оно
чётное и делится на 3.
15 762 - чётное и сумма его цифр делится на 3 (1+5+7+6+2 = 21, 21 : 3 = 7); 15762 :6=2627;
2. Признак делимости на12. Число делится на 12, если оно делится на 3 и на 4.
412356 (оканчивается на 56, 56:4=14; и сумма его цифр делится на 3: 4+1+2+3+5+6=21; 21:3=7); 412356:12=34363;
3. Признак делимости на 15. Число делится на 15, если оно делится на 3 и на 5.
56190 (оканчивается на 0 и сумма его цифр делится на 3: 5+6+1+9+0=21, 21:3=7); 56190:15=3746.
4. Признак делимости на 7. Число делится на 7, если результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
364 делится на 7,так как 36–(2*4)=28; 28:7=4.
15 762 - чётное и сумма его цифр делится на 3 (1+5+7+6+2 = 21, 21 : 3 = 7); 15762 :6=2627;
2. Признак делимости на12. Число делится на 12, если оно делится на 3 и на 4.
412356 (оканчивается на 56, 56:4=14; и сумма его цифр делится на 3: 4+1+2+3+5+6=21; 21:3=7); 412356:12=34363;
3. Признак делимости на 15. Число делится на 15, если оно делится на 3 и на 5.
56190 (оканчивается на 0 и сумма его цифр делится на 3: 5+6+1+9+0=21, 21:3=7); 56190:15=3746.
4. Признак делимости на 7. Число делится на 7, если результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
364 делится на 7,так как 36–(2*4)=28; 28:7=4.
Признаки делимости составных чисел.
Слайд 13
5. Признак делимости на 13. Число делится на 13, если число
его десятков, сложенное с учетверенным числом единиц, кратно 13.
416 делится на 13, так как 41+(4*6)=41+24=65; 65:13=5.
6. Признак делимости на 14. Число делится на 14, если оно делится и на 2, и на 7.
518-чётное, делится на 2, 51-8*2=51-16=35 (35:7=5) – делится на 7; 518:14=37.
7. Признак делимости на 19. Число делится на 19, если число его десятков, сложенное с удвоенным числом единиц, кратно 19.
646 делится на 19, так как 64+(2*6)=76, 76:19=4; 646:19=34.
8. Признак делимости на 99. Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп. Если эта сумма делится на 99, то и само число делится на 99.
56732544 делится на 99, так как 56+73+25+44=198, 198:99=2
416 делится на 13, так как 41+(4*6)=41+24=65; 65:13=5.
6. Признак делимости на 14. Число делится на 14, если оно делится и на 2, и на 7.
518-чётное, делится на 2, 51-8*2=51-16=35 (35:7=5) – делится на 7; 518:14=37.
7. Признак делимости на 19. Число делится на 19, если число его десятков, сложенное с удвоенным числом единиц, кратно 19.
646 делится на 19, так как 64+(2*6)=76, 76:19=4; 646:19=34.
8. Признак делимости на 99. Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп. Если эта сумма делится на 99, то и само число делится на 99.
56732544 делится на 99, так как 56+73+25+44=198, 198:99=2
Слайд 14Пиёмы быстрого деление и умножении чисел
Деление на 2. Иногда удобно число, которое
делим представить в виде суммы или разности полных десятков и числа .
398:2=(400-2):2=(400:2)-(2:2)=200-1=199
714:2=(700+14):2=700:2+14:2=350+7=357;
Деление и умножение на 4 и 8. Чтобы число разделить на 4, надо дважды разделить это число на 2.
81264: 4=(81264:2):2=40632:2=20316
Чтобы умножить число на 4, надо последовательно двукратно умножить это число на 2.
153*4=153*2*2=306*2=612
Деление (или умножение) на 8 являются трехкратным делением (или умножением) на 2.
57200:8=57200:2:2:2=28600:2:2=14300:2=7150
237*8=237*2*2*2=474*2*2=948*2=1896
398:2=(400-2):2=(400:2)-(2:2)=200-1=199
714:2=(700+14):2=700:2+14:2=350+7=357;
Деление и умножение на 4 и 8. Чтобы число разделить на 4, надо дважды разделить это число на 2.
81264: 4=(81264:2):2=40632:2=20316
Чтобы умножить число на 4, надо последовательно двукратно умножить это число на 2.
153*4=153*2*2=306*2=612
Деление (или умножение) на 8 являются трехкратным делением (или умножением) на 2.
57200:8=57200:2:2:2=28600:2:2=14300:2=7150
237*8=237*2*2*2=474*2*2=948*2=1896
Слайд 15
Деление и умножение на 5. Чтобы любое число разделить на 5,
его нужно умножить на 2 и разделить на 10.
326:5= 326*2:10=652:10=65,2
Чтобы число умножить на 5, можно его разделить на 2 и умножить частное на 10: 876*5=876:2*10=438*10=4380
Умножение (деление) на25 аналогично.
120*25 = 120:4*100=30*100=3000.
43:25=43*4:100=172:100=1,72
Деление 1000 на 2, 4, 8, 16. Полезно знать деление чисел, кратных 10 на числа, кратные двум: 1000=2*500=4*250=8*125=16*62,5.
Умножение на 9. Чтобы умножить число на 9 можно сначала умножить это число на 10, а затем вычесть из результата само число. 89*9=89*10-89=890-89=801
326:5= 326*2:10=652:10=65,2
Чтобы число умножить на 5, можно его разделить на 2 и умножить частное на 10: 876*5=876:2*10=438*10=4380
Умножение (деление) на25 аналогично.
120*25 = 120:4*100=30*100=3000.
43:25=43*4:100=172:100=1,72
Деление 1000 на 2, 4, 8, 16. Полезно знать деление чисел, кратных 10 на числа, кратные двум: 1000=2*500=4*250=8*125=16*62,5.
Умножение на 9. Чтобы умножить число на 9 можно сначала умножить это число на 10, а затем вычесть из результата само число. 89*9=89*10-89=890-89=801
Слайд 16Умножение на 11.
1 способ. Чтобы, умножить число на 11, необходимо множимое
умножить на 10 и прибавить множимое,
67*11=67*10+67=670+67=737.
2 способ. Следует «раздвинуть» цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд.
53*11=5(5+3)3=583
74*11=7( 7+4)4=7(11)4=814, единицу помещаем между восьмеркой (семерка плюс перенесенная единица) и четверкой.
67*11=67*10+67=670+67=737.
2 способ. Следует «раздвинуть» цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд.
53*11=5(5+3)3=583
74*11=7( 7+4)4=7(11)4=814, единицу помещаем между восьмеркой (семерка плюс перенесенная единица) и четверкой.
Слайд 17Умножение на 111, 1111, 11111 (для двузначных чисел, сумма цифр которых
меньше 10)
Чтобы умножить число на 111, 1111, 11111 и так далее нужно цифры этого числа «раздвинуть» на 2, 3 и так далее шагов, в образовавшийся промежуток вписать сумму этих цифр, 2, 3 и так далее раз.
51*111=5(5+1)(5+1)1=5661
26*1111=2(2+6)(2+6)(2+6)6=28886
Чтобы умножить число на 111, 1111, 11111 и так далее нужно цифры этого числа «раздвинуть» на 2, 3 и так далее шагов, в образовавшийся промежуток вписать сумму этих цифр, 2, 3 и так далее раз.
51*111=5(5+1)(5+1)1=5661
26*1111=2(2+6)(2+6)(2+6)6=28886
Слайд 18Метод дополнения до 100
98 * 97=….
| |
2 3
добавляем число, недостающее до 100 98 и 97
2*3=6 умножаем эти числа, записываем в конце произведения 06. Находим разность между любым из чисел и недостатком до 100 другого числа. 98-3=95; 97-2=95. В обоих случаях разности одинаковы. Записываем разность перед 06. Получившееся число и есть искомое произведение.
98*97=9506
2 3
добавляем число, недостающее до 100 98 и 97
2*3=6 умножаем эти числа, записываем в конце произведения 06. Находим разность между любым из чисел и недостатком до 100 другого числа. 98-3=95; 97-2=95. В обоих случаях разности одинаковы. Записываем разность перед 06. Получившееся число и есть искомое произведение.
98*97=9506
Слайд 19462=(25-4)*100+42=2100+16=2116
4-дополнение до 50
532=(25+3)*100+32=2809
3-разница между 53 и 50
Метод дополнения до 50
Слайд 20 Если запомнить квадраты всех чисел от
1 до 25, то легко найти и квадрат любого двузначного числа, превышающего 25.
Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю.
Примеры:
1. 372=(37-25)*100+(50-37)2=12*100+132=1200+169=1369
2. 722=(72-25)*100+(72-50)2=47*100+222=4700+484=5184
Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю.
Примеры:
1. 372=(37-25)*100+(50-37)2=12*100+132=1200+169=1369
2. 722=(72-25)*100+(72-50)2=47*100+222=4700+484=5184
Возведение в квадрат любого двузначного числа.
Слайд 21При возведении чисел в квадрат удобно используя формулы сокращенного умножения.
372=(30+7)2=302+2*30*7+72
282=(30-2)2=302-2*30*2+22=900-120+4=784
Рассмотрим
и другие приёмы возведения в квадрат
Возведение в квадрат чисел от 40 до50.
Чтобы возвести в квадрат число пятого десятка (41,42,43,44,45,46,47,48,49), нужно к числу единиц прибавить 15, умножить на 100, затем к полученному числу прибавить квадрат дополнения числа единиц до 10 (если этот квадрат - однозначное число, то перед ним приписывается число о)
432=(3+15)*100+(10-3)2=1800+49=1849 482=(8+15)*100+(10-8)2=2300+ 4=2304
Возведение в квадрат чисел от 40 до50.
Чтобы возвести в квадрат число пятого десятка (41,42,43,44,45,46,47,48,49), нужно к числу единиц прибавить 15, умножить на 100, затем к полученному числу прибавить квадрат дополнения числа единиц до 10 (если этот квадрат - однозначное число, то перед ним приписывается число о)
432=(3+15)*100+(10-3)2=1800+49=1849 482=(8+15)*100+(10-8)2=2300+ 4=2304
Слайд 22Чтобы возвести в квадрат число шестого десятка (51,52,53,54,55,56,57,58,59) надо к числу единиц прибавить
25 и к этой сумме приписать квадрат числа единиц.
Например:
542=(4+25)*100+4*4=2916
572=(7+25)*100+7*7=3249
Возведение в квадрат числа, оканчивающееся на 5.
Число десятков умножаем на следующее за ним натуральное число и приписываем 25.
152=(1*2)25=225; 352=(3*4)25=1225 ; 652=(6*7)25=4225
Возведение в квадрат числа, оканчивающееся на 5.
Число десятков умножаем на следующее за ним натуральное число и приписываем 25.
152=(1*2)25=225; 352=(3*4)25=1225 ; 652=(6*7)25=4225
Возведение в квадрат чисел от 50 до 60.
Слайд 23Квадрат числа, оканчивающегося на 1
При возведении в
квадрат числа, оканчивающегося на 1, нужно заменить эту единицу на 0, возвести новое число в квадрат и прибавить к этому квадрату исходное число и число, полученное заменой 1 на 0.
712 =702+70+71=4900+141=5041
Квадрат числа, оканчивающегося на 6.
При возведении в квадрат числа, оканчивающегося на 6, нужно заменить цифру 6 на 5, возвести новое число в квадрат (оканчивающееся на 5) и прибавить к этому квадрату исходное число и число, полученное заменой 6 на 5.
562 =552+55+56=3025+55+56=3080+56=3136
712 =702+70+71=4900+141=5041
Квадрат числа, оканчивающегося на 6.
При возведении в квадрат числа, оканчивающегося на 6, нужно заменить цифру 6 на 5, возвести новое число в квадрат (оканчивающееся на 5) и прибавить к этому квадрату исходное число и число, полученное заменой 6 на 5.
562 =552+55+56=3025+55+56=3080+56=3136
Слайд 24Квадрат числа, оканчивающегося на 9.
При возведении в
квадрат числа, оканчивающегося на 9, нужно заменить эту цифру 9 на 0 (получим следующее натуральное число), возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное заменой 9 на 0.
592=602-60-59=3600–60–59=3481
Квадрат числа, оканчивающегося на 4.
При возведении в квадрат числа, оканчивающегося на 4, нужно заменить цифру 4 на 5, возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное заменой 4 на 5.
842=852-85-84=7225-85-84=7056
592=602-60-59=3600–60–59=3481
Квадрат числа, оканчивающегося на 4.
При возведении в квадрат числа, оканчивающегося на 4, нужно заменить цифру 4 на 5, возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное заменой 4 на 5.
842=852-85-84=7225-85-84=7056