- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Применение производной к исследованию функций
Содержание
- 1. Презентация по математике Применение производной к исследованию функций
- 2. Применение производной к исследованию функций и построению графиковТема урока:
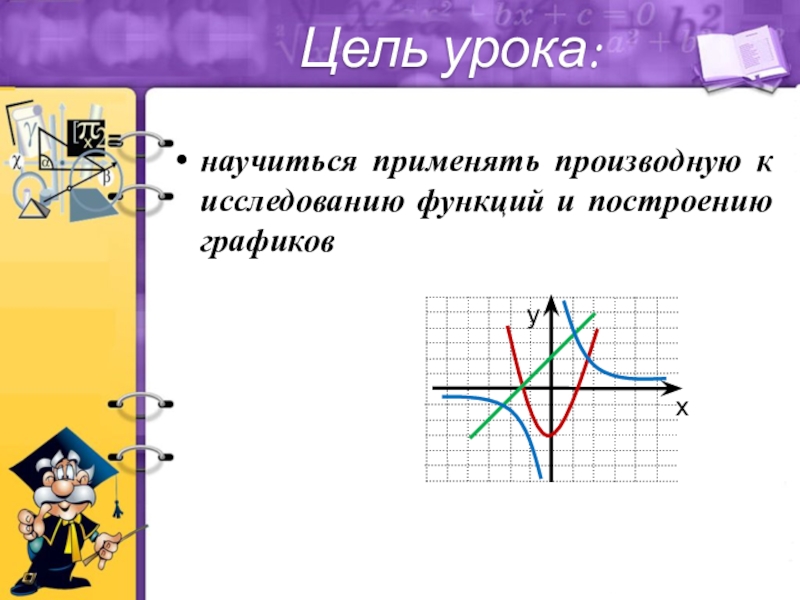
- 3. научиться применять производную к исследованию функций и построению графиковЦель урока:
- 4. «Музыка может возвышать или умиротворять душу,живопись –
- 5. Знания иметь отличные,исследуя функции различные!
- 6. «Кто смолоду делает и думает сам, тот становиться потом надежнее, крепче, умнее» В. Шукшин.
- 7. Найдите производную функции:
- 8. ВзаимопроверкаНормы оценок:5 правильных ответов – «5»4 правильных
- 9. Контрольные вопросы:1) Какая функция называется возрастающей?2) Какая функция называется убывающей?
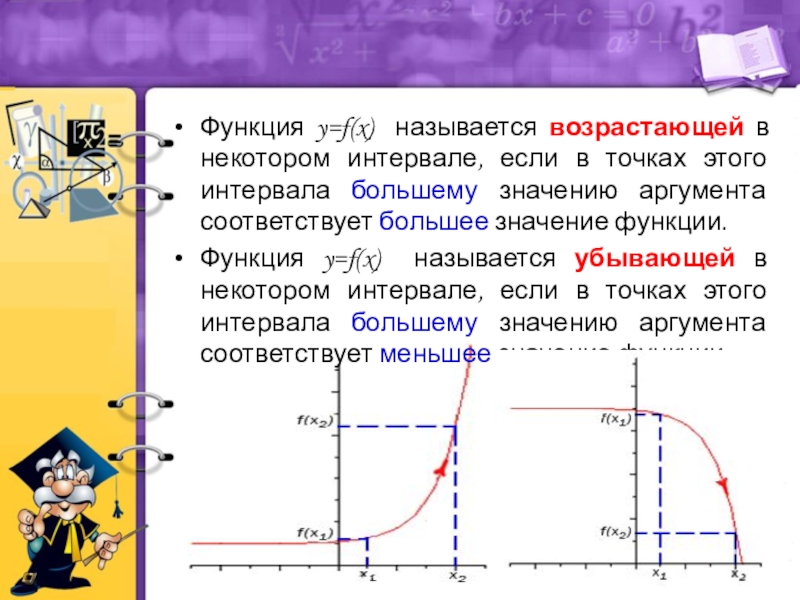
- 10. Функция y=f(x) называется возрастающей в некотором интервале,
- 11. Контрольные вопросы:3) Какая точка называется точкой минимума функции?4) Какая точка называется точкой максимума функции?
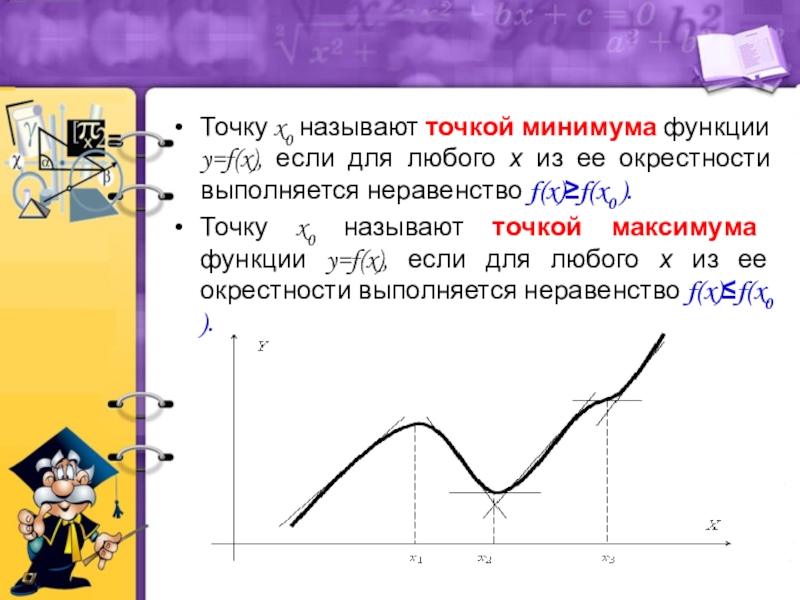
- 12. Точку x0 называют точкой минимума функции y=f(x),
- 13. Контрольные вопросы:5) В чем заключается геометрический смысл производной?
- 14. Геометрический смысл производной:Производная функции f(x) в точке
- 15. СамооценкаОцените долю своего участия в устной работе:
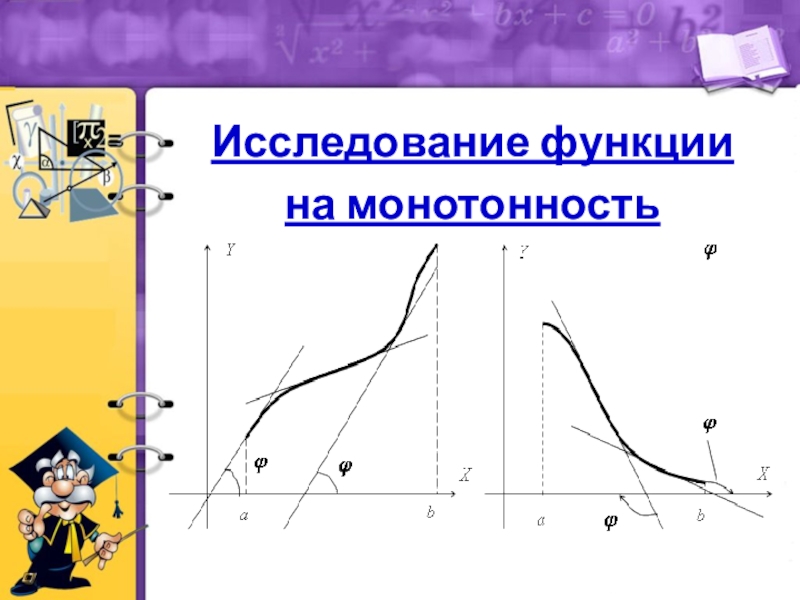
- 16. Исследование функции на монотонность
- 17. Если дифференцируемая функция y=f(x) возрастает (убывает) в
- 18. Если производная функции y=f(x) положительна (отрицательна) на
- 19. Находим область определения функции f(x).Вычисляем производную f’(x)
- 20. Область определения: D(y)=R. Вычисляем производную : y’=6x²-6x-36.Находим
- 21. Область определения: D(y)=R. Вычисляем производную : y’=3x²-6x.Находим
- 22. Исследование функции на экстремумы
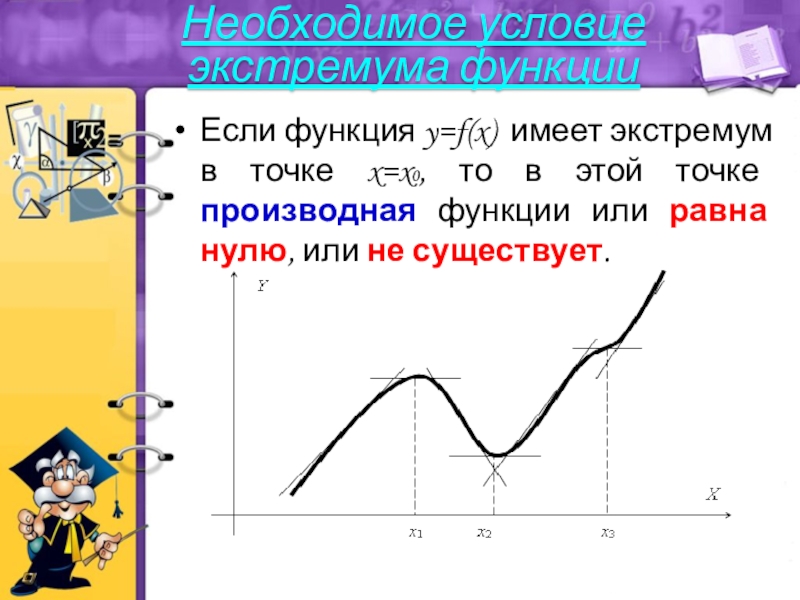
- 23. Если функция y=f(x) имеет экстремум в точке
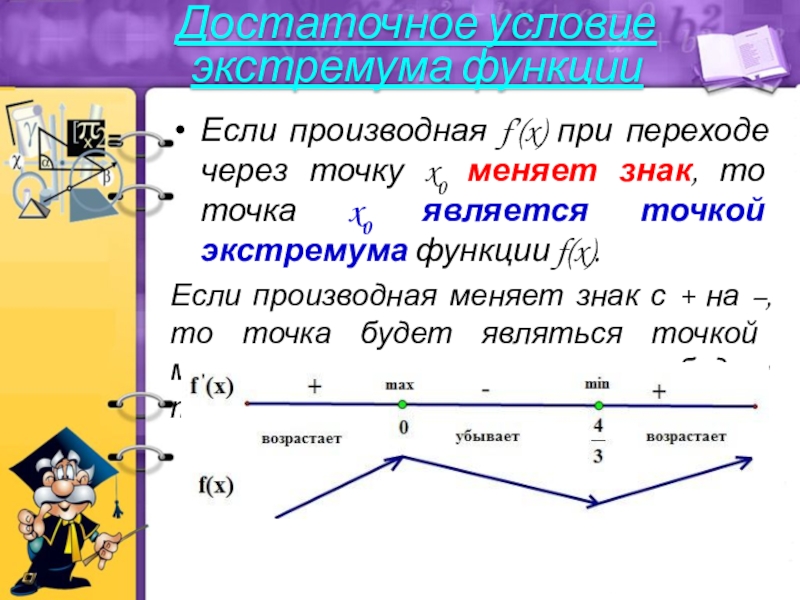
- 24. Если производная f’(x) при переходе через точку
- 25. Правило нахождения экстремумов функцииНаходим область определения функции
- 26. Область определения: D(y)=R. Вычисляем производную : y’=-6x²-6x+12.Находим
- 27. Слайд 27
- 28. Закрепление: Устно. Докажите, что функция
- 29. Найдите интервалы монотонности функции: 1) 2) Закрепление:
- 30. Закрепление:Устно. Определите характер поведения функции
- 31. Закрепление: Найдите промежутки монотонности и экстремумы
- 32. Работа в группахНайдите промежутки монотонности и экстремумы
- 33. Коррекция знанийАнализ ошибок, допущенных при выполнении самостоятельной работы.
- 34. Повторение учебного содержанияНеобходимое условие возрастания (убывания) функции.Достаточное
- 35. Применение производной в различных областях знанийПрезентация
- 36. Домашнее задание1. Выучите конспект.2. Найдите интервалы монотонности
- 37. Рефлексия
- 38. Удачи!
Применение производной к исследованию функций и построению графиковТема урока:
Слайд 1С помощью производной:
1) Найдите промежутки монотонности функции y=2x³-3x²-36x+5.
2) Найдите экстремумы функции
y=-2x³-3x²+12x+6.
3) Найдите промежутки монотонности и экстремумы функции
и постройте схематический график.
Слайд 4«Музыка может возвышать или умиротворять душу,
живопись – радовать глаз,
поэзия – пробуждать
чувства,
философия – удовлетворять потребности разума, инженерное дело –совершенствовать материальную сторону жизни людей, а математика способна достичь всех этих целей!»
Морис Клайн
философия – удовлетворять потребности разума, инженерное дело –совершенствовать материальную сторону жизни людей, а математика способна достичь всех этих целей!»
Морис Клайн
Слайд 8Взаимопроверка
Нормы оценок:
5 правильных ответов – «5»
4 правильных ответа – «4»
3 правильных
ответа – «3»
0 – 2 правильных ответа – «2».
0 – 2 правильных ответа – «2».
Слайд 9Контрольные вопросы:
1) Какая функция называется возрастающей?
2) Какая функция называется убывающей?
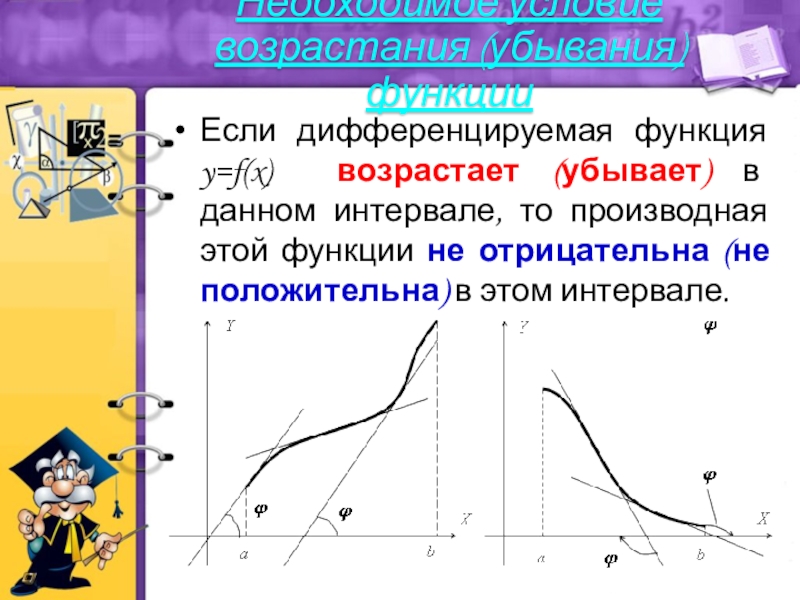
Слайд 10Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого
интервала большему значению аргумента соответствует большее значение функции.
Функция y=f(x) называется убывающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует меньшее значение функции.
Функция y=f(x) называется убывающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует меньшее значение функции.
Слайд 11Контрольные вопросы:
3) Какая точка называется точкой минимума функции?
4) Какая точка называется
точкой максимума функции?
Слайд 12Точку x0 называют точкой минимума функции y=f(x), если для любого х
из ее окрестности выполняется неравенство f(x)≥f(x0 ).
Точку x0 называют точкой максимума функции y=f(x), если для любого х из ее окрестности выполняется неравенство f(x)≤f(x0 ).
Точку x0 называют точкой максимума функции y=f(x), если для любого х из ее окрестности выполняется неравенство f(x)≤f(x0 ).
Слайд 14Геометрический смысл
производной:
Производная функции f(x) в точке x0 равна угловому коэффициенту
касательной, проведенной к графику функции f(x) в точке
(x0; f(x0)), т.е.
f’(x0)=k=tgα.
(x0; f(x0)), т.е.
f’(x0)=k=tgα.
Слайд 15Самооценка
Оцените долю своего участия в устной работе:
Активно поднимали руку, и
вам удалось ответить правильно, оценка – «5»,
ваши ответы были правильными, но вы сомневались и стеснялись – «4»,
были неточности – «3»,
вы были пассивны – «2».
ваши ответы были правильными, но вы сомневались и стеснялись – «4»,
были неточности – «3»,
вы были пассивны – «2».
Слайд 17Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная
этой функции не отрицательна (не положительна) в этом интервале.
Необходимое условие
возрастания (убывания) функции
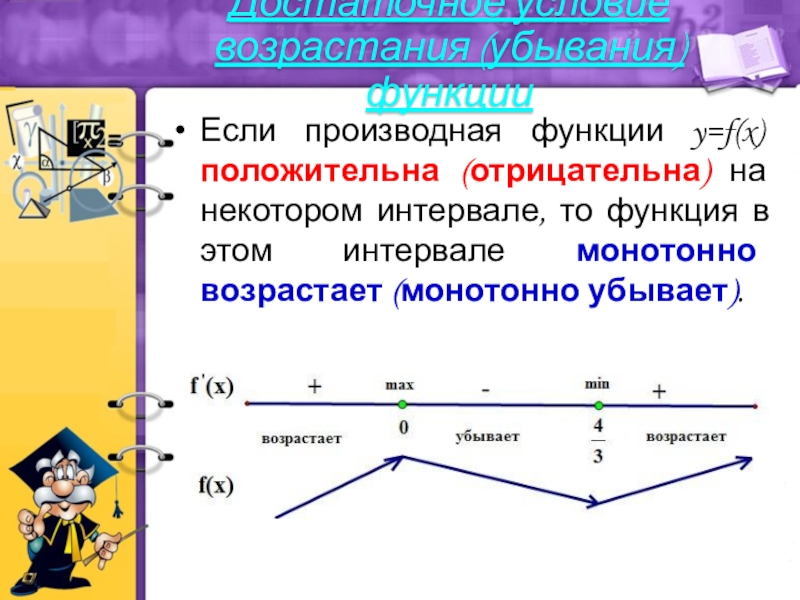
Слайд 18Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция
в этом интервале монотонно возрастает (монотонно убывает).
Достаточное условие возрастания (убывания) функции
Слайд 19Находим область определения функции f(x).
Вычисляем производную f’(x) данной функции.
Находим точки, в
которых f’(x)=0 или не существует. Эти точки называются критическими для функции f(x).
Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.
Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.
Правило нахождения интервалов монотонности
Слайд 20Область определения: D(y)=R.
Вычисляем производную : y’=6x²-6x-36.
Находим критические точки: y’=0.
x²-x-6=0
Д=1-4*(-6)*1=1+24=25
Делим
область определения на интервалы:
Функция возрастает при xϵ(-∞;-2]υ[3;+∞), функция убывает при xϵ[-2;3].
Функция возрастает при xϵ(-∞;-2]υ[3;+∞), функция убывает при xϵ[-2;3].
Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5
+
+
-
-2
3
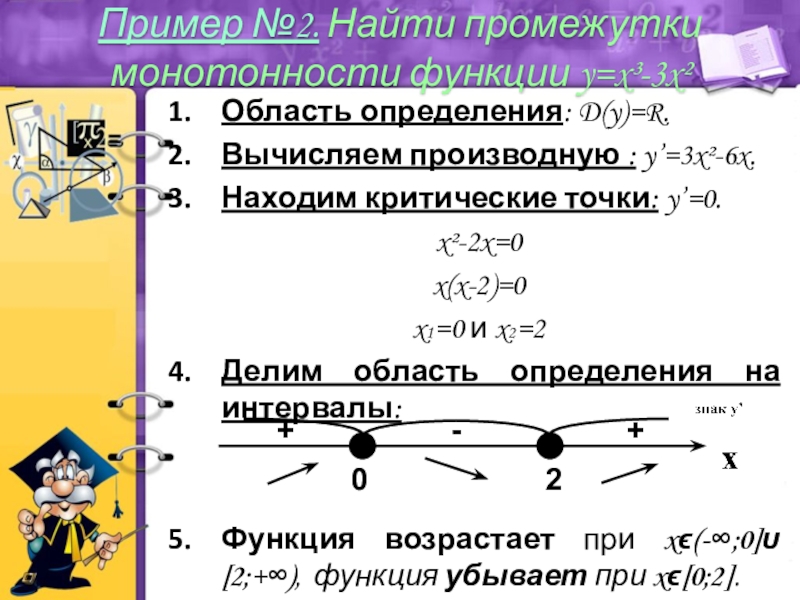
Слайд 21Область определения: D(y)=R.
Вычисляем производную : y’=3x²-6x.
Находим критические точки: y’=0.
x²-2x=0
x(x-2)=0
x1=0
и x2=2
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].
Пример №2. Найти промежутки монотонности функции y=x³-3x²
+
+
-
0
2
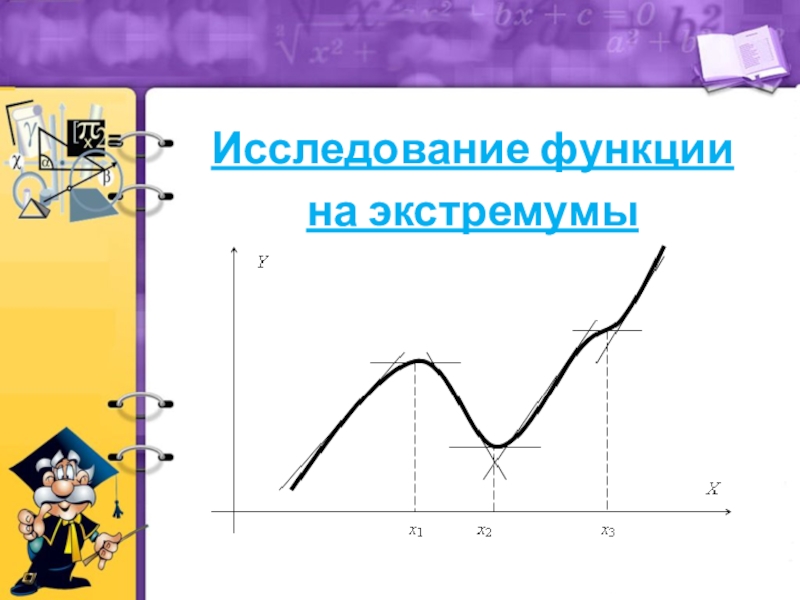
Слайд 23Если функция y=f(x) имеет экстремум в точке x=x0, то в этой
точке производная функции или равна нулю, или не существует.
Необходимое условие экстремума функции
Слайд 24Если производная f’(x) при переходе через точку x0 меняет знак, то
точка x0 является точкой экстремума функции f(x).
Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума
Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума
Достаточное условие экстремума функции
Слайд 25Правило нахождения экстремумов функции
Находим область определения функции f(x).
Вычисляем производную f’(x) данной
функции.
Находим критические точки функции f(x).
Делим область определения функции этими точками на интервалы монотонности.
Исследуем знак f’(x) на каждом интервале. Если f’(x) при переходе через точку x0 меняет знак, то x0 является точкой экстремума функции f(x). Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума. Вычисляем экстремальное значение.
Находим критические точки функции f(x).
Делим область определения функции этими точками на интервалы монотонности.
Исследуем знак f’(x) на каждом интервале. Если f’(x) при переходе через точку x0 меняет знак, то x0 является точкой экстремума функции f(x). Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума. Вычисляем экстремальное значение.
Слайд 26Область определения: D(y)=R.
Вычисляем производную : y’=-6x²-6x+12.
Находим критические точки: y’=0.
-x²-x+2=0
Д=1-4*(-1)*2=1+8=9
x1=1;
x2=-2
Делим область определения на интервалы:
min max
5. x=-2 – точка минимума. Найдём минимум функции ymin= -14. x=1 – точка максимума. Найдём максимум функции: ymax=13.
Делим область определения на интервалы:
min max
5. x=-2 – точка минимума. Найдём минимум функции ymin= -14. x=1 – точка максимума. Найдём максимум функции: ymax=13.
Пример №3. Найти экстремумы функции
y=-2x³-3x²+12x+6
-
-
+
-2
1
Слайд 28Закрепление:
Устно. Докажите, что функция
f(x)
= 3х3 + 5 возрастает для любого значения аргумента.
Слайд 31Закрепление:
Найдите промежутки
монотонности и экстремумы
функции
и постройте схематический график
Слайд 32Работа в группах
Найдите промежутки монотонности и экстремумы функции и постройте схематический
график:
на оценку «3» на оценку «4»
на оценку «5»
Самопроверка по листу эталонных ответов. Самооценка.
на оценку «3» на оценку «4»
на оценку «5»
Самопроверка по листу эталонных ответов. Самооценка.
Слайд 34Повторение учебного содержания
Необходимое условие возрастания (убывания) функции.
Достаточное условие возрастания (убывания) функции.
Правило
нахождения интервалов монотонности функции.
Необходимое условие экстремума функции.
Достаточное условие экстремума функции.
Правило нахождения экстремумов функции.
Необходимое условие экстремума функции.
Достаточное условие экстремума функции.
Правило нахождения экстремумов функции.
Слайд 36Домашнее задание
1. Выучите конспект.
2. Найдите интервалы монотонности функции:
3. Исследуйте на
экстремумы функцию и постройте схематический график
