- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Преобразование графиков функций (10 класс)
Содержание
- 1. Презентация по математике Преобразование графиков функций (10 класс)
- 2. Как будет выглядеть график данной функции???
- 3. Преобразование графиков функций
- 4. Цель:1.Научится строить график функции y=sinx и y=cosx2.
- 5. Слайд 5
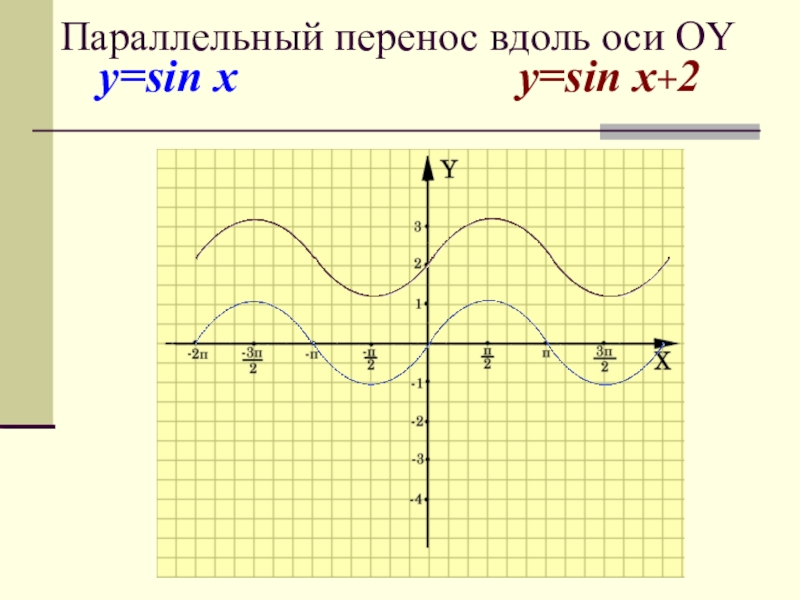
- 6. Параллельный перенос вдоль оси OY на A единиц:* вверх, если А>0, * вниз, если А
- 7. y=sin x
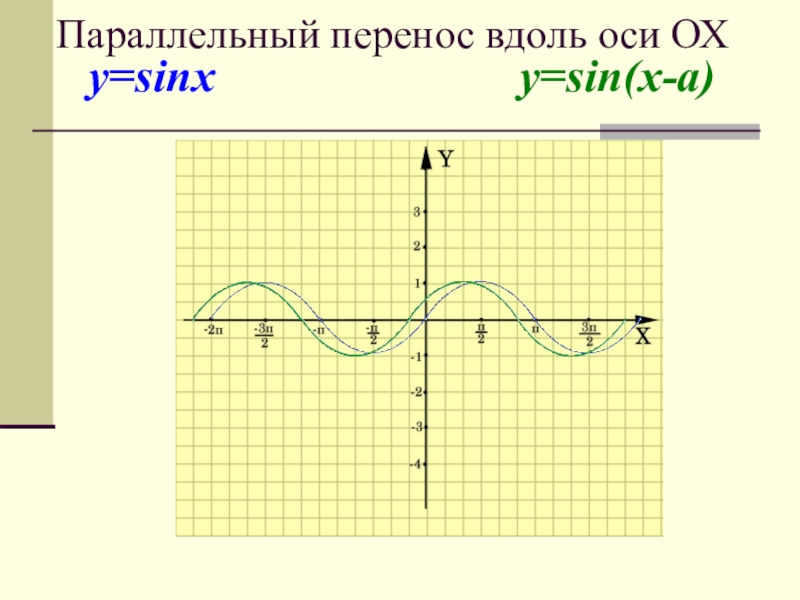
- 8. Параллельный перенос вдоль оси OХ на A единиц:* вправо, если a > 0, * влево, если a < 0.
- 9. y=sinx
- 10. * Растяжение вдоль оси OY относительно оси
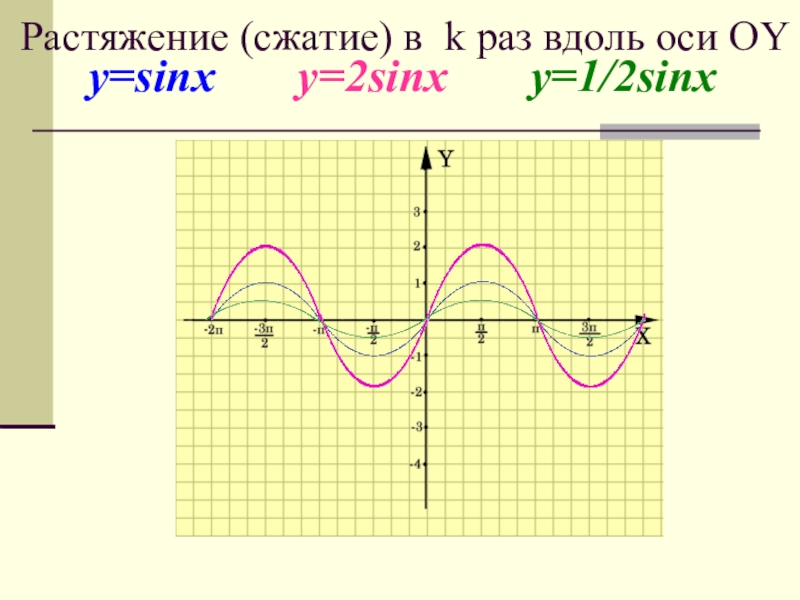
- 11. y=sinx y=2sinx y=1/2sinxРастяжение (сжатие) в k раз вдоль оси OY
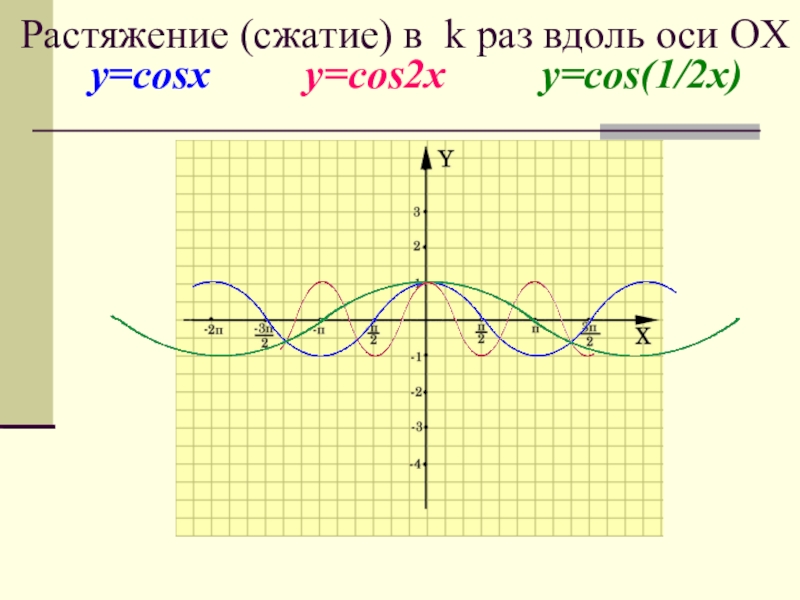
- 12. * Сжатие вдоль оси OX относительно оси
- 13. y=cosx y=cos2x
- 14. Симметричное отражение относительно оси OX
- 15. y=cosx
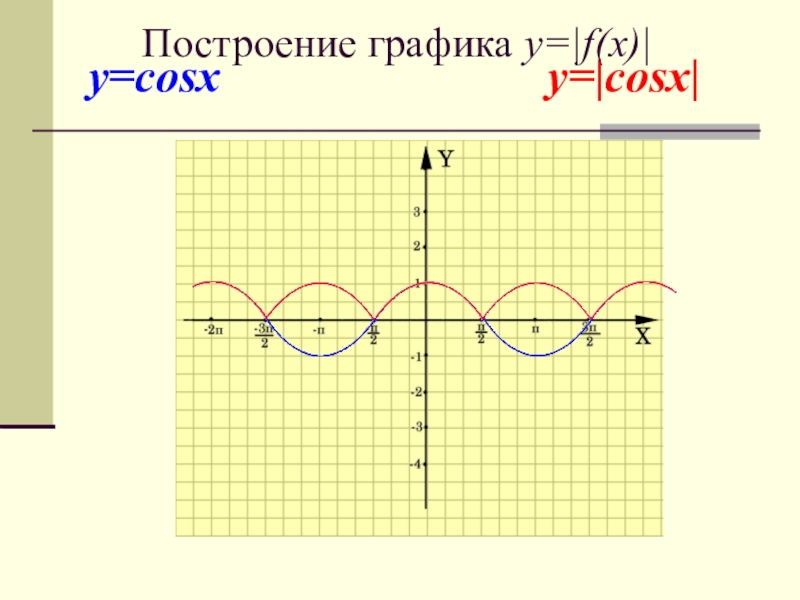
- 16. Часть графика, расположенная ниже оси OX, симметрично
- 17. y=cosx
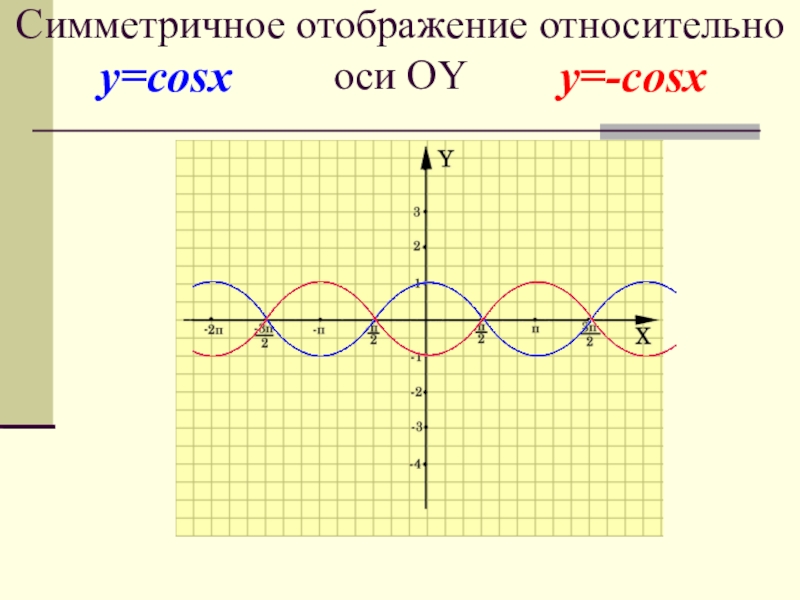
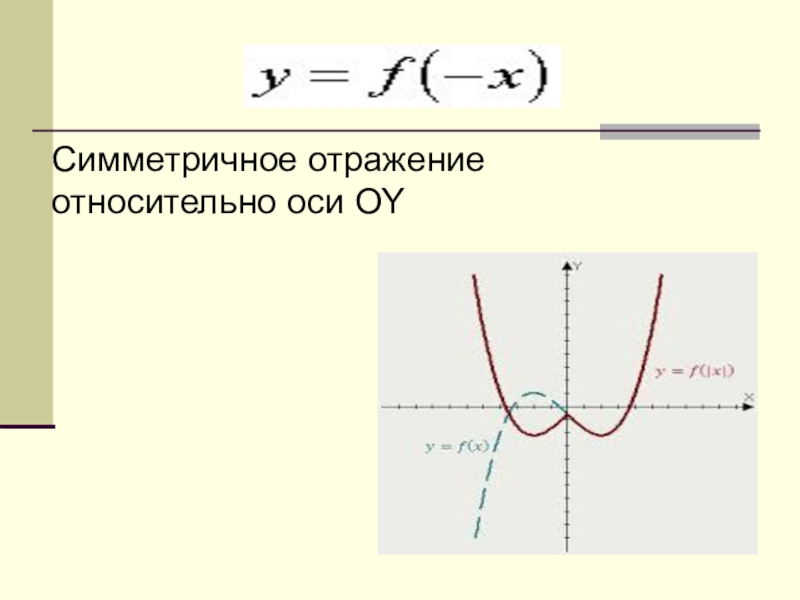
- 18. Симметричное отражение относительно оси OY
- 19. Какие преобразования нужно выполнить для:
- 20. 1. Построить график функции: y=sinx2. Растянуть вдоль
- 21. Построение графиков функций y=sinx и y=cosx
- 22. 00ππxxyy011α1α2α3α3α2α11Масштаб π:3α4α4α5α5α6α6На оси абсцисс координатной плоскости Оху
- 23. xy10Масштаб π:3На практике, для построения графика функции
- 24. xy10Масштаб π:3−1Используя равенство cosx=sin(
- 25. Слайд 25
- 26. ·сегодня я узнал… · теперь я могу…
- 27. ДомаВыполнить построение в тетради
- 28. Спасибозавнимание
Слайд 4Цель:
1.Научится строить график функции y=sinx и y=cosx
2. Обобщить и систематизировать знания
3. Посмотреть построение графика функции, зная порядок преобразований функции
Слайд 10* Растяжение вдоль оси OY относительно оси OX в k раз, если k
* Сжатие вдоль оси OY относительно оси OX в 1/kраз, если 0 < k < 1.
Слайд 12* Сжатие вдоль оси OX относительно оси OY в k раз, если k
* Растяжение вдоль оси OX относительно оси OY в 1/kраз, если 0 < k < 1.
Слайд 16Часть графика, расположенная ниже оси OX, симметрично отражается относительно этой оси,
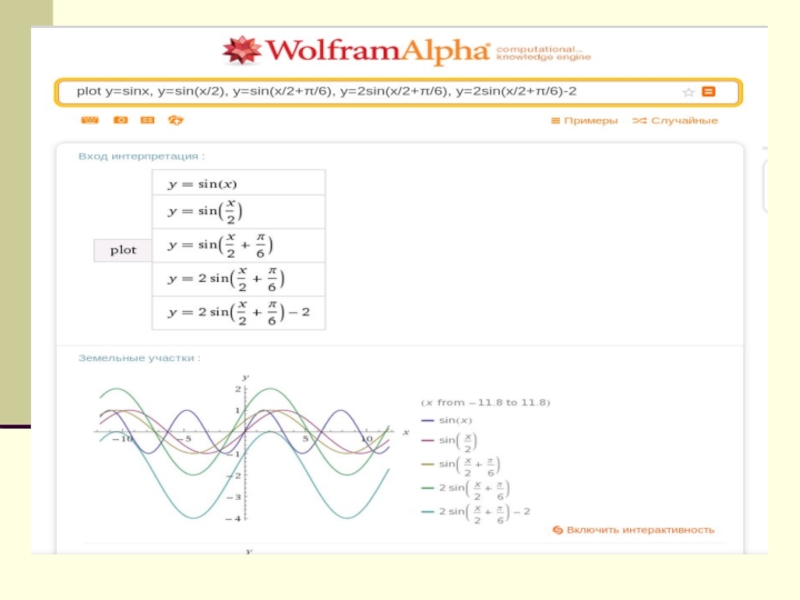
Слайд 201. Построить график функции: y=sinx
2. Растянуть вдоль оси Ох в 2
y=sinx/2
3. Параллельно перенести вдоль оси Ох на П/6 вправо:
y=sin(x/2+П/6)
4. Растянуть в 2 раза вдоль оси Оу:
y=2sin(x/2+П/6)
5. Параллельный перенос вдоль оси Оу вниз на 1:
y=2sin(x/2+П/6)-1
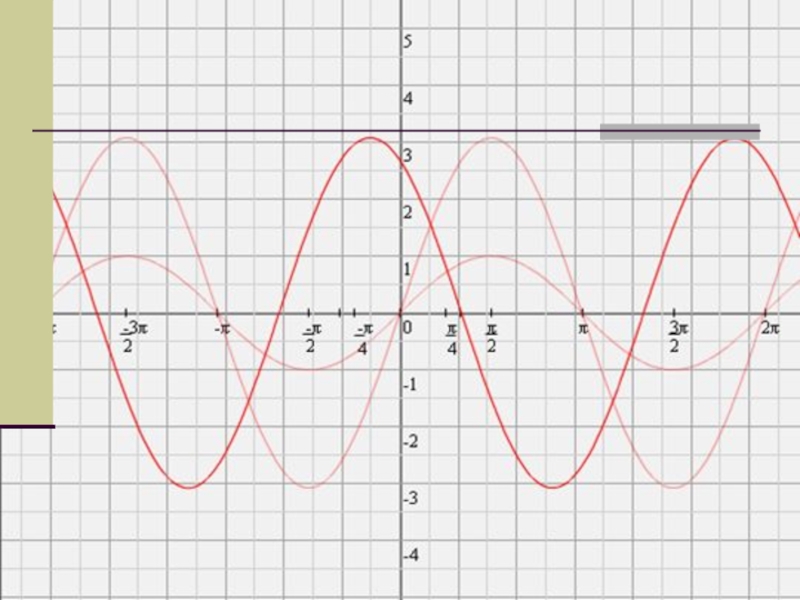
6. Отобразить отрицательные части вдоль оси Ох:
y=|2sin(x/2+П/6)-1|
Слайд 22
0
0
π
π
x
x
y
y
0
1
1
α1
α2
α3
α3
α2
α1
1
Масштаб π:3
α4
α4
α5
α5
α6
α6
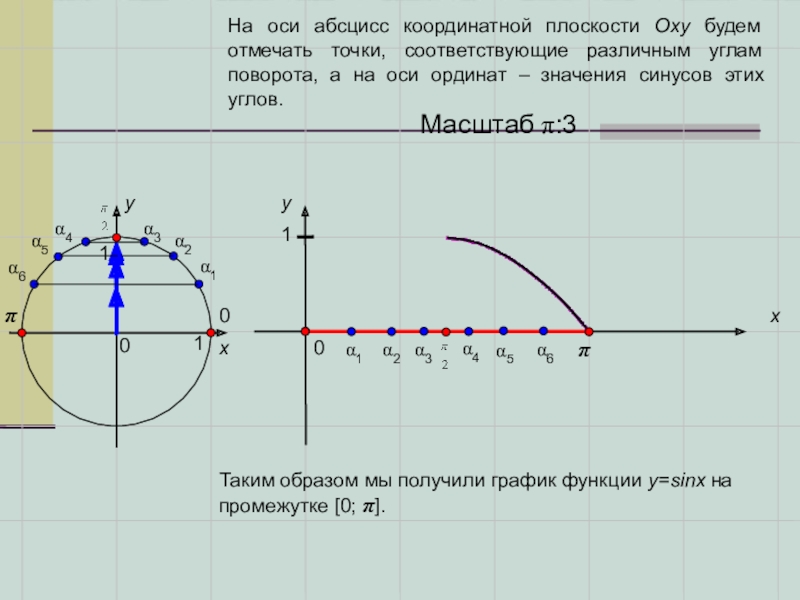
На оси абсцисс координатной плоскости Оху будем отмечать точки, соответствующие
Таким образом мы получили график функции y=sinx на промежутке [0; π].
Слайд 23x
y
1
0
Масштаб π:3
На практике, для построения графика функции у=sinx на промежутке [0;
После этого используют свойство периодичности функции у=sinx. Так как наименьший положительный период функции y=sinx равен 2π, то изображенный участок графика можно параллельно переносить влево и вправо вдоль оси Ох на 2π⋅n (n∈) единичных отрезков.
−1
График функции y=sinx называется синусоидой.
Слайд 24x
y
1
0
Масштаб π:3
−1
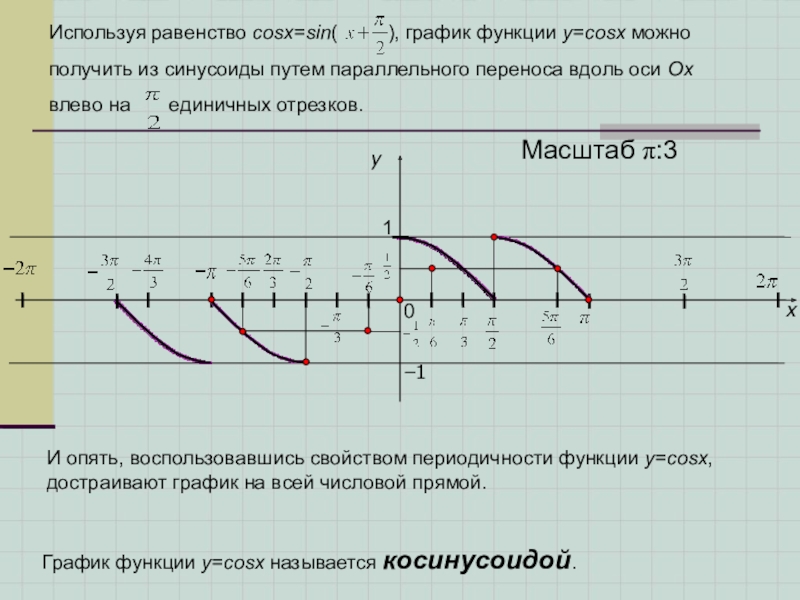
Используя равенство cosx=sin( ), график функции
получить из синусоиды путем параллельного переноса вдоль оси Ох
влево на единичных отрезков.
И опять, воспользовавшись свойством периодичности функции y=cosx, достраивают график на всей числовой прямой.
График функции y=cosx называется косинусоидой.
Слайд 26·сегодня я узнал…
· теперь я могу…
· я почувствовал, что…
· я научился…
· у меня получилось …
Подведем итоги:
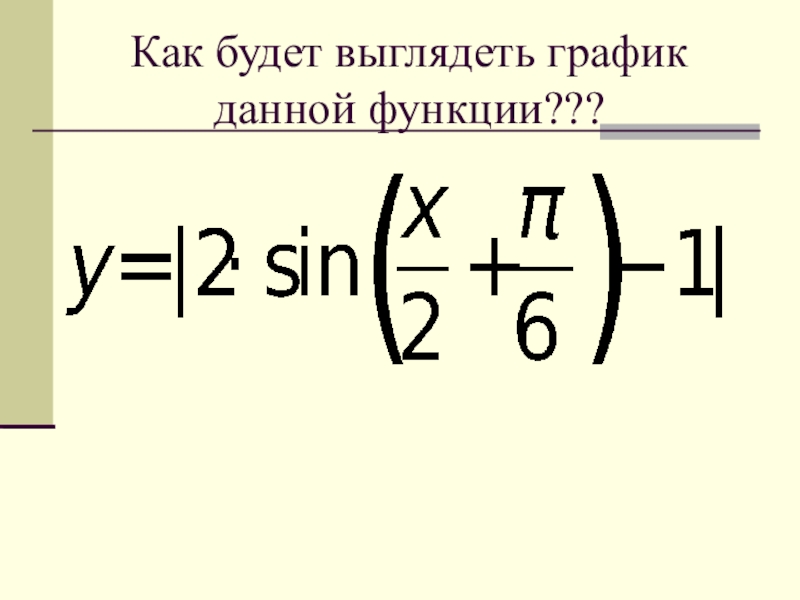












![Презентация по математике Преобразование графиков функций (10 класс) xy10Масштаб π:3На практике, для построения графика функции у=sinx на промежутке [0; xy10Масштаб π:3На практике, для построения графика функции у=sinx на промежутке [0; π], сначала отмечают точки с координатами](/img/thumbs/2399e5fe9625673ac28ee7246959c285-800x.jpg)