- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Понятие о развитие числа (11 класс, 1 курс СПО)
Содержание
- 1. Презентация по математике Понятие о развитие числа (11 класс, 1 курс СПО)
- 2. ДействительныечислаРациональныечислаЦелые числаНатуральныечислаNZQRКомплексныечислаС
- 3. Для счета предметов используются числа , которые
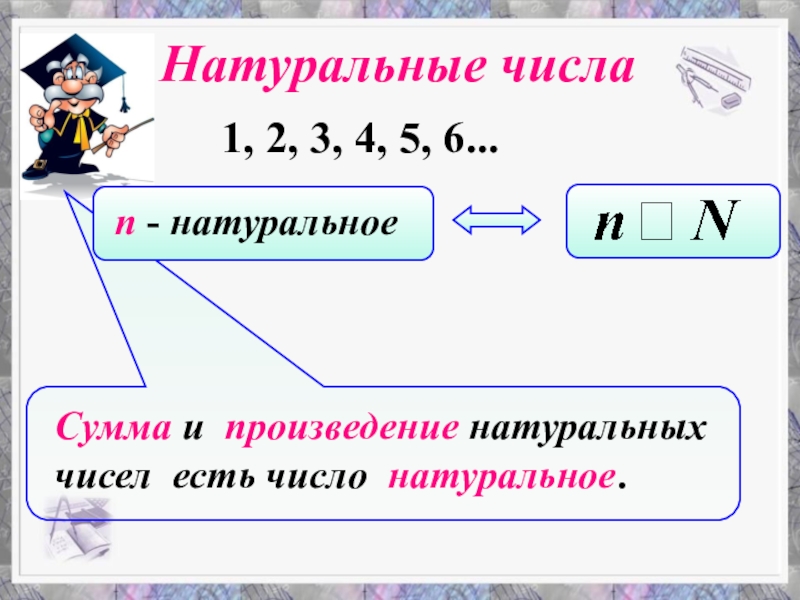
- 4. Натуральные числа1, 2, 3, 4, 5, 6...
- 5. Целые числаЦелыми числами называют множество натуральных чисел,
- 6. Отрицательные числа ввели в математический обиход Михаэль
- 7. Натуральные числаЧисла,им противоположныеЦелые
- 8. Целые числа…-3;-2;-1;0,1, 2, 3,... m - целое
- 9. Слайд 9
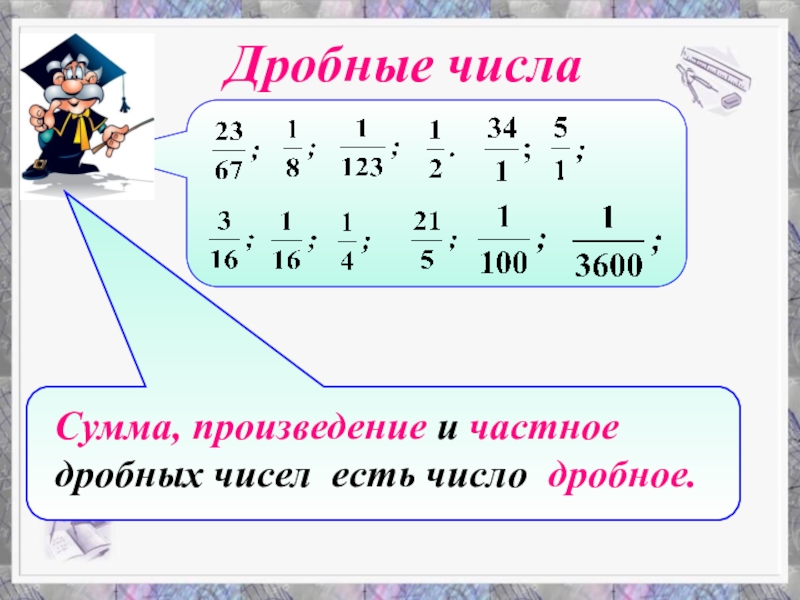
- 10. Дробные числа
- 11. Целые числаДробные числаРациональные
- 12. Выполнить действия Ответы
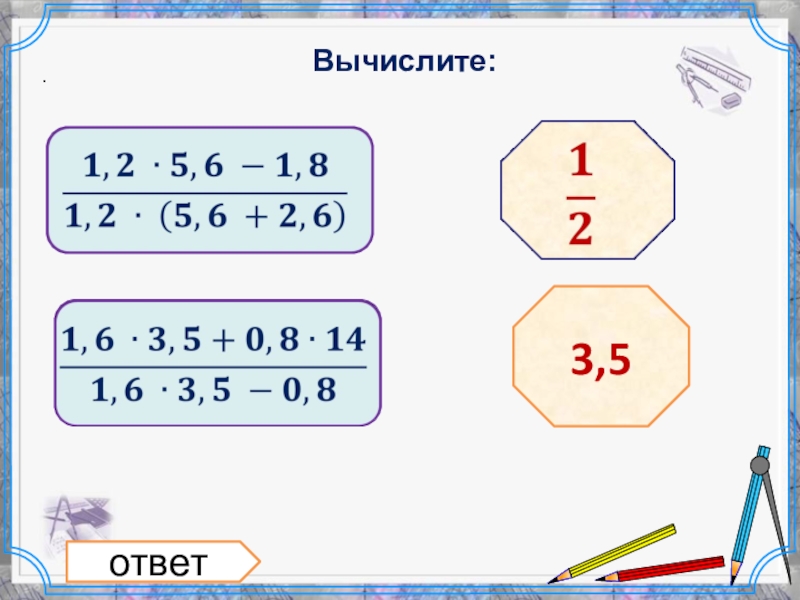
- 13. Вычислите:. ответ 3,5
- 14. Рациональные числа
- 15. Слайд 15
- 16. Ничего, не зная об открытии ал –
- 17. Замените данные рациональные числадесятичными дробями.
- 18. 0,(2)=291 цифра0,(81)=812 цифры99
- 19. Чтобы обратить смешанную периодическую дробь в обыкновенную,
- 20. Пример. Записать в виде обыкновенной дроби бесконечную
- 21. Положим х=1,5(23)=1,52323…Сначала умножим на 10. Получим 15,2323..,
- 22. ПОНЯТИЕ О РАЗВИТИЕ ЧИСЛАДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
- 23. Числа, которые не являются рациональными, то есть
- 24. Иррациональные числаМножество иррациональных чисел обозначается I.Например:Бесконечная непериодическая дробь называется иррациональным числом.
- 25. ДействительныечислаРациональныечислаЦелые числаНатуральныечислаNZQRКомплексныечислаСIИррациональноечисла
- 26. Действительные числаR=(рациональные числа, иррациональные числа)Действительные числа не обладают свойством замкнутости - не всякое уравнение имеет корни.
- 27. Слайд 27
- 28. Вариант 11. Записать в виде
- 29. Слайд 29
ДействительныечислаРациональныечислаЦелые числаНатуральныечислаNZQRКомплексныечислаС
Слайд 3Для счета предметов используются числа , которые называются натуральными. Для обозначения
множества натуральных чисел употребляется буква N -первая буква латинского слова Naturalis, «естественный», «натуральный»
Слайд 5Целые числа
Целыми числами называют множество натуральных чисел, им противоположных и число
нуль.
Z=(1,2,3,4,5,6,7,8…
-1,-2,-3,-4,-5,-6,-7,-8…, 0)
Z=(1,2,3,4,5,6,7,8…
-1,-2,-3,-4,-5,-6,-7,-8…, 0)
Слайд 6Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная
арифметика» (1544),
и Никола Шюке (1445—1500)-
его работа была обнаружена в 1848 году.
и Никола Шюке (1445—1500)-
его работа была обнаружена в 1848 году.
Слайд 16Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй
раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).
Слайд 19Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной
дроби
поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
0,4(6)=
4
6
4
1 цифра
9
1 цифра
0
Слайд 20Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.
Положим, что
х=1,(23), т.е. 1,232323…
100х=123,2323…
100х=123,2323…
х=1,2323…
99х=122
х=
Итак: 1,(23)=
100х=123,2323…
100х=123,2323…
х=1,2323…
99х=122
х=
Итак: 1,(23)=
Слайд 21Положим х=1,5(23)=1,52323…
Сначала умножим на 10.
Получим 15,2323.., а потом ещё на
100
1000х=1523,2323…
10х= 5,232323…
990х=1508
х=
Итак: 1,5(23)=
1000х=1523,2323…
10х= 5,232323…
990х=1508
х=
Итак: 1,5(23)=
Слайд 23Числа, которые не являются рациональными, то есть не являются ни целыми,
ни представимыми в виде дроби вида , где m – целое число, а n – натуральное, называются иррациональными.
Слайд 24Иррациональные числа
Множество иррациональных чисел обозначается I.
Например:
Бесконечная непериодическая дробь называется иррациональным числом.
Слайд 25Действительные
числа
Рациональные
числа
Целые числа
Натуральные
числа
N
Z
Q
R
Комплексные
числа
С
I
Иррациональное
числа
Слайд 26Действительные числа
R=(рациональные числа, иррациональные числа)
Действительные числа не обладают свойством замкнутости -
не всякое уравнение имеет корни.
Слайд 28Вариант 1
1. Записать в виде
а)
б)
2.Представьте в виде
а) 15,(3)
б) 2,(14)
в) 1,6(1)
2.Представьте в виде
а) 15,(3)
б) 2,(14)
в) 1,6(1)
Вариант 2
бесконечной дроби
а) б)
обыкновенной дроби
а) 7,(2)
б) 23,(25)
в) 3,9(12)
Самостоятельная работа