- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Комбинаторные задачи. Правило умножения (9 класс)
Содержание
- 1. Презентация по математике по теме Комбинаторные задачи. Правило умножения (9 класс)
- 2. Комбинаторные задачи напоминают игру в кубики. Имеется
- 3. Все возможные варианты нетрудно выписать: (организованный перебор)На
- 4. Решение можно оформить по-другому: С помощью дерева
- 5. Второй пример: «В алфавите племени уауа
- 6. Решение: перебор вариантов 8 слов!
- 7. Дерево возможных вариантов В алфавите племени уауа имеются
- 8. «Правило умножения»Для того чтобы найти число всех
- 9. Третий пример: «На завтрак Вова может выбрать
- 10. Решение 3*4=12 вариантов!
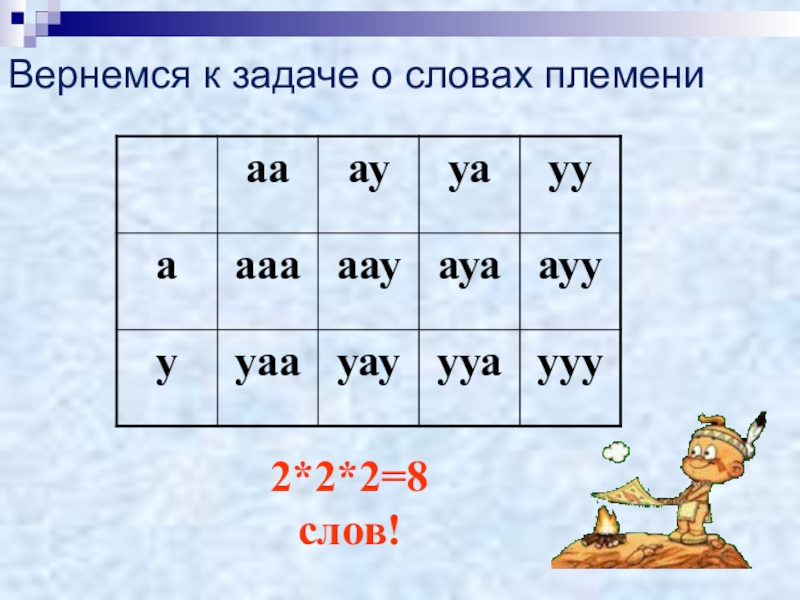
- 11. Вернемся к задаче о словах племени2*2*2=8 слов!
- 12. №4. Сколько чётных двузначных чисел можно составить
- 13. №5 «Этот вечер свободный можно так провести…»: Пойти
- 14. №6 В коридоре - 3 лампочки. Сколько
- 15. Подводим итоги! В данных примерах был осуществлен способ
- 16. Спасибо завнимание
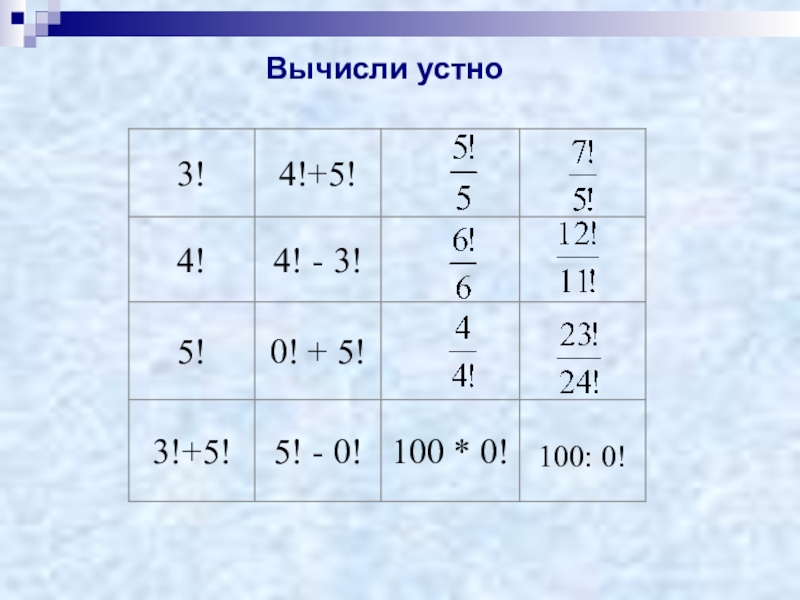
- 17. 100: 0!Вычисли устно
Комбинаторные задачи напоминают игру в кубики. Имеется конечное число кубиков, нужно посчитать количество комбинаций составленных из этих кубиков. Рассмотрим первый пример. Из данных цифр нужно составить трехзначное число без повторяющихся цифр.
Слайд 1Простейшие
комбинаторные
задачи.
Автор - учитель математики МОУ СОШ №4
Василенко О.Ю.
Правило умножения
Слайд 2Комбинаторные задачи напоминают игру в кубики. Имеется конечное число кубиков, нужно
посчитать количество комбинаций составленных из этих кубиков.
Рассмотрим первый пример.
Из данных цифр нужно составить трехзначное число без повторяющихся цифр.
Слайд 3Все возможные варианты нетрудно выписать: (организованный перебор)
На первом месте фиксируем цифру
1 получим два числа
На первом месте фиксируем цифру 4 получим два числа
На первом месте фиксируем цифру 7 получим два числа
Получили 2+2+2=2*3=6
На первом месте фиксируем цифру 4 получим два числа
На первом месте фиксируем цифру 7 получим два числа
Получили 2+2+2=2*3=6
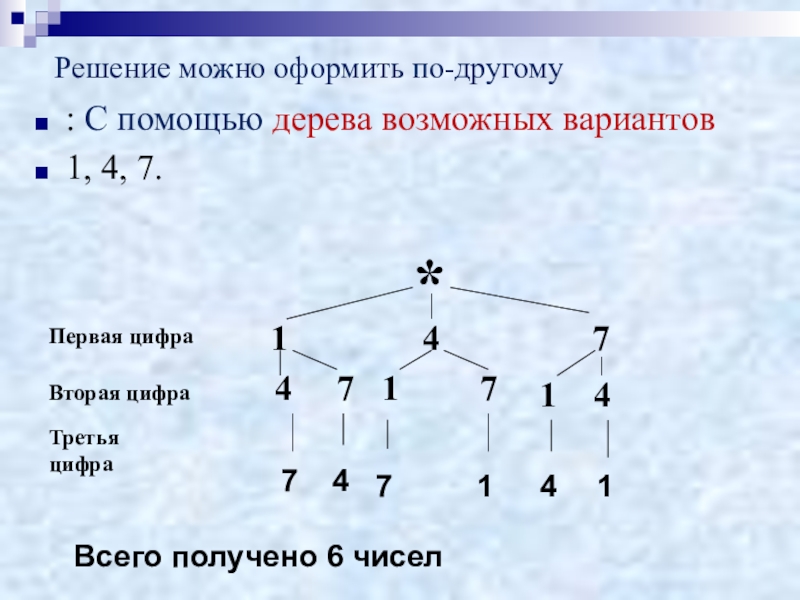
Слайд 4Решение можно оформить по-другому
: С помощью дерева возможных вариантов
1, 4, 7.
*
Первая цифра
Вторая цифра
Третья цифра
7
4
7
1
4
1
Всего получено 6 чисел
Слайд 5 Второй пример: «В алфавите племени уауа имеются только две буквы
– «а» и «у».
Сколько различных слов по три буквы в каждом слове можно составить, используя алфавит этого племени?»
Сколько различных слов по три буквы в каждом слове можно составить, используя алфавит этого племени?»
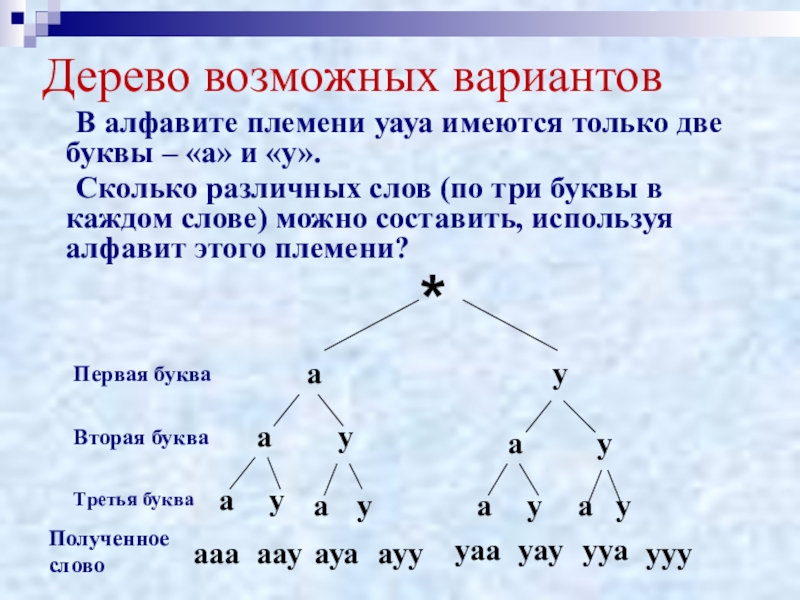
Слайд 7Дерево возможных вариантов
В алфавите племени уауа имеются только две буквы –
«а» и «у».
Сколько различных слов (по три буквы в каждом слове) можно составить, используя алфавит этого племени?
Сколько различных слов (по три буквы в каждом слове) можно составить, используя алфавит этого племени?
*
Первая буква
Вторая буква
Третья буква
Полученное слово
Слайд 8«Правило умножения»
Для того чтобы найти число всех возможных исходов независимого проведения
испытаний А, В и C следует перемножить число всех исходов испытания А на число всех исходов испытания В и на число все исходов испытания С.
А· В· С
А· В· С
Слайд 9 Третий пример: «На завтрак Вова может выбрать плюшку, бутерброд, пряник или
кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбрать?»
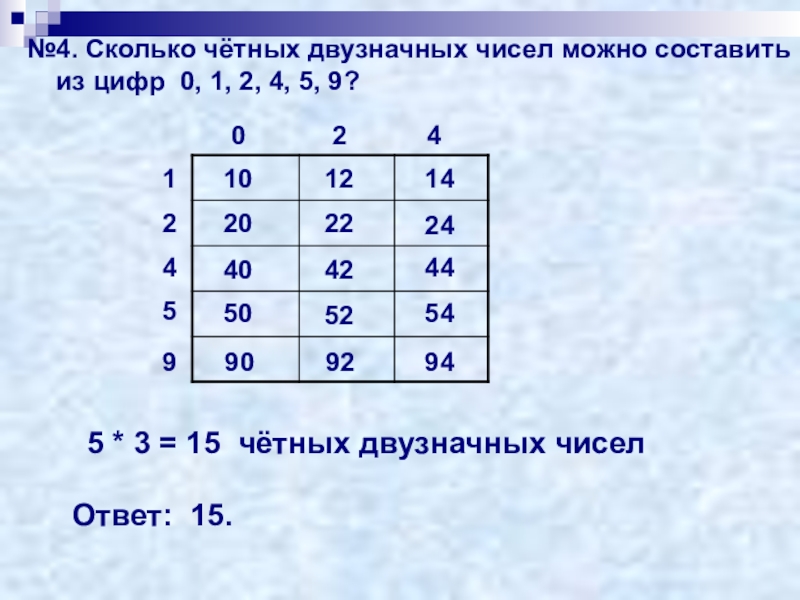
Слайд 12№4. Сколько чётных двузначных чисел можно составить
из цифр
0, 1, 2, 4, 5, 9?
1
2
4
5
9
0
2
4
10
20
40
50
90
12
22
42
52
92
14
24
44
54
94
5 * 3 = 15 чётных двузначных чисел
Ответ: 15.
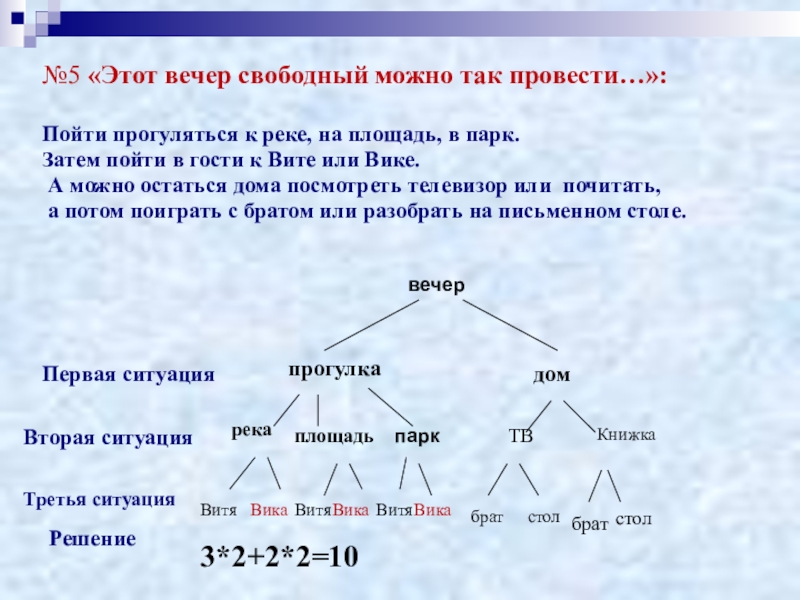
Слайд 13№5 «Этот вечер свободный можно так провести…»:
Пойти прогуляться к реке, на
площадь, в парк.
Затем пойти в гости к Вите или Вике.
А можно остаться дома посмотреть телевизор или почитать,
а потом поиграть с братом или разобрать на письменном столе.
Затем пойти в гости к Вите или Вике.
А можно остаться дома посмотреть телевизор или почитать,
а потом поиграть с братом или разобрать на письменном столе.
вечер
Первая ситуация
Вторая ситуация
Третья ситуация
Решение
3*2+2*2=10
парк
Витя
Вика
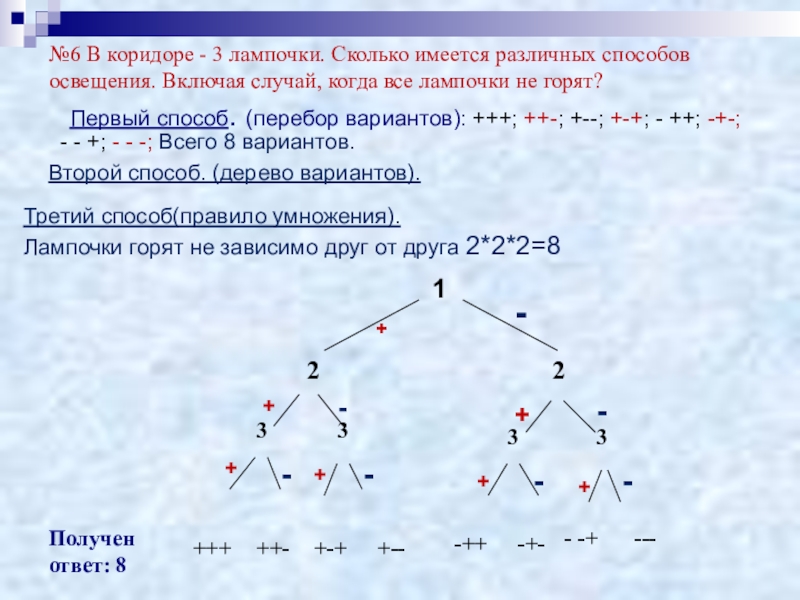
Слайд 14№6 В коридоре - 3 лампочки. Сколько имеется различных способов освещения.
Включая случай, когда все лампочки не горят?
Первый способ. (перебор вариантов): +++; ++-; +--; +-+; - ++; -+-; - - +; - - -; Всего 8 вариантов.
1
Получен ответ: 8
Второй способ. (дерево вариантов).
Третий способ(правило умножения).
Лампочки горят не зависимо друг от друга 2*2*2=8
+
-
+
-
+
-
+
+
+
+
-
-
-
-
Слайд 15Подводим итоги!
В данных примерах был осуществлен способ перебора возможных вариантов (возможных
комбинаций).
Поэтому данные задачи называют комбинаторными.
Решения данных задач основывается на общем правиле умножения.
Поэтому данные задачи называют комбинаторными.
Решения данных задач основывается на общем правиле умножения.
