- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Первообразная
Содержание
- 1. Презентация по математике Первообразная
- 2. АннотацияОзнакомление с историей возникновения и развития интегрального
- 3. Историческая справкаВы познакомились в этой теме с
- 4. Знаки интеграла и дифференцирования , были впервые
- 5. Слайд 5
- 6. Если f – непрерывная и неотрицательная на
- 7. Пример: Вычислить площадь криволинейной трапеции, ограниченной линиями
- 8. С помощью интеграла в физике решается большое
- 9. Дифференциальное уравнение – это уравнение, содержащее производную
- 10. Решение многих физических задач сводится к решению
- 11. Принцип Кавальери. Нахождение объёма шара с помощью
- 12. Объем шараТеоремаДоказательствоxCAMOxRBОбъем шара радиуса R равен 4/3πR3Рассмотрим
Слайд 2Аннотация
Ознакомление с историей возникновения и развития интегрального исчисления
применение интегралов к решения
Подготовка к контрольной работе и ТВН
Слайд 3Историческая справка
Вы познакомились в этой теме с самыми началами интегрального
исчисления, служащего
дифференциального исчисления.
Первые работы по открытию интегрального исчисления принадлежат еще
Архимеду – первому математику древности.
В средние века этой проблемой занимался итальянский ученый Кавальери.
Но подлинное открытие интегрального исчисления принадлежит двум великим
ученым XVII века – Ньютону и Лейбницу.
Архимед
Ковальери
Ньютон
Лейбниц
Слайд 4Знаки интеграла и дифференцирования , были впервые использованы Лейбницем в конце
Интеграл в древности
Интегрирование прослеживается ещё в древнем Египте, примерно в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпыванияметод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.
Слайд 5
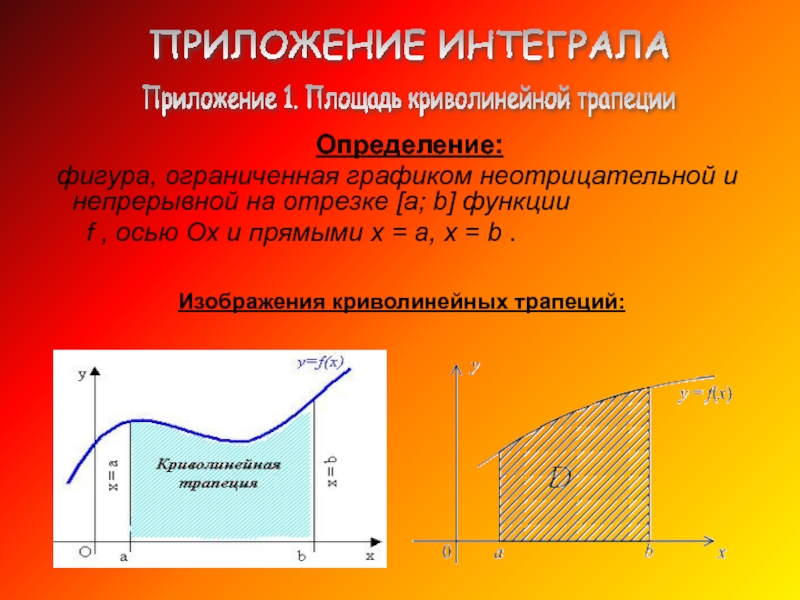
фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a; b] функции
f , осью Ох и прямыми х = а, х = b .
ПРИЛОЖЕНИЕ ИНТЕГРАЛА
Изображения криволинейных трапеций:
Приложение 1. Площадь криволинейной трапеции
Слайд 6
Если f – непрерывная и неотрицательная на отрезке [a; b]
функция ,
Теорема:
Теорема о вычислении площади криволинейной трапеции
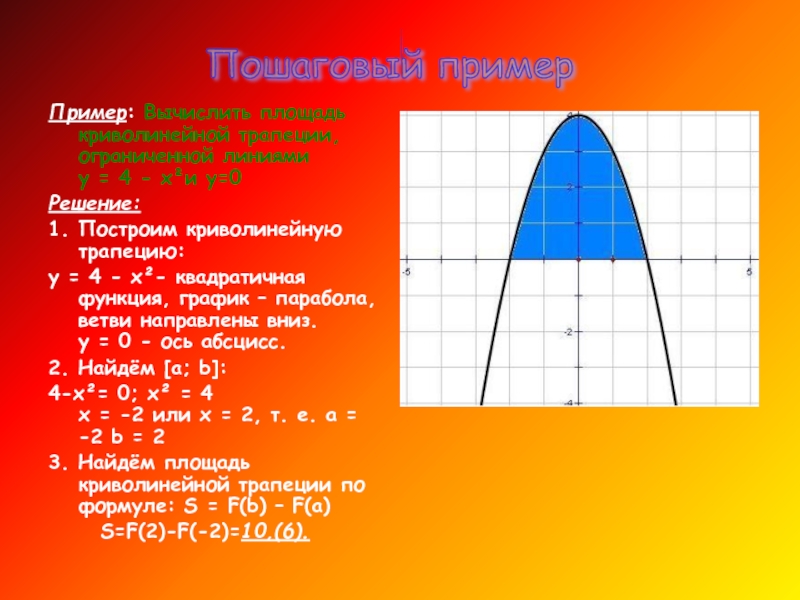
Слайд 7Пример: Вычислить площадь криволинейной трапеции, ограниченной линиями
Решение:
1. Построим криволинейную трапецию:
у = 4 - х²- квадратичная функция, график – парабола, ветви направлены вниз. у = 0 - ось абсцисс.
2. Найдём [а; b]:
4-х²= 0; х² = 4 х = -2 или х = 2, т. е. а = -2 b = 2
3. Найдём площадь криволинейной трапеции по формуле: S = F(b) – F(а)
S=F(2)-F(-2)=10,(6).
Пошаговый пример
Слайд 8С помощью интеграла в физике решается большое количество задач на определение
t1 b S = ∫U(t)dt и A = ∫ F(x)dx t0 a
Например:
Вычислить работу силы F при сжатии пружины на 0,08 м, если для ее сжатия на 0,01 м требуется сила 10Н.
Решение: по закону Гука сила F пропорциональна растяжению или сжатию пружины, т.е. F=kx, где х - величина растяжения или сжатия (в м); k – постоянная. Из условия находим k. Так как при x=0,01 м, F=10н, то k=F/x=1000.
Следовательно: F(x)=kx=1000x.
Работа силы F(x) при перемещении тела из точки а в точку b равна:
b A= ∫ F(x)dx a
Используем данные и получаем:
0,08 0,08 A= ∫ 1000xdx = 1000 х²/2 | = 3,2 (дж). 0 0
Приложение 2.
Слайд 9Дифференциальное уравнение – это уравнение, содержащее производную неизвестной функции.
Решить дифференциальное уравнение
Но решение дифференциального уравнения определяется неоднозначно. Поэтому для его решения требуется дополнительное условие.
Например: уравнение Y = x+1 – это дифференциальное уравнение.
Требуется найти функцию Y(x), производная от которой равна х+1.
Т.е. найти первообразную. Тогда первообразная Y = x2/2 + x + c, где с – постоянная – общее решение.
Если взять условие, что Y(0) = 3, то находим: 3 = 0 + 0 + с или с=3.
Тогда Y(x)= x2/2 + x + 3 – частное решение.
В практике часто встречаются процессы, которые периодически повторяются: колебательные движения маятника, струны, пружины и т.д., т.е. процессы связанны с переменным электрическим током, магнитным полем.
Решение таких задач сводится к решению дифференциального уравнения.
Y``= -ω2y – дифференциальное уравнение гармоничных колебаний.
ω – заданное положительное число.
Y= y`(x) Y``= (y`(x))`
Решением являются функции:
Y(x) = Asin(ωx + φ)
A – амплитуда колебания.
ω – частота, φ – начальная фаза.
Графиком гармонических колебаний является синусоида.
Например: Y(x) = 2sin(2x + π/2).
Приложение 3.
Слайд 10Решение многих физических задач сводится к решению дифференциального равнения.
Y` = ky,
Решением этого уравнения является функция
Y = C℮ⁿ, где С – постоянная, определяемая условием конкретной задачи, n=kx.
Например:
Скорость m`(t) размножения бактерий связана с массой m(t) бактерий в момент времени t .
Уравнением: m`(t) = km(t), где k – положительное число, зависящее от вида бактерий и внешних условий.
Решениями этого уравнения является функция: m(t) = C℮ⁿ, n=kx
Постоянную С можно найти, например, из условия, что в момент t=0 масса m0 бактерий известна.
Тогда m(0) = m0 = C℮º = C и поэтому m(t) = m0℮ⁿ, n=kt.
Приложение 4.
Приложение 4.
Слайд 11Принцип Кавальери. Нахождение объёма шара с помощью принципа Кавальери
В Европе
Интерес математиков сосредотачивался главным образом на общих принципах определения объемов тел вращения с помощью бесконечно малых величин.
Среди таких математиков был итальянский монах Бонавентура Кавальери (1598-1647). Он занимал кафедру математики в Болонском университете. У Кавальери в 1635 г. вышла книга «Геометрия, изложенная новым способом при помощи неделимых частей непрерывных величин». При вычислении объемов фигур бывает полезно преобразовывать фигуры, не меняя их объемов, например, разрезать на части и составлять новые (так называемые равносоставленные фигуры).
Принцип Кавальери довольно близок к другому методу нахождения объёмов тел – методу интегрирования.
Приложение 5.
Слайд 12Объем шара
Теорема
Доказательство
x
C
A
M
O
x
R
B
Объем шара радиуса R равен 4/3πR3
Рассмотрим шар радиуса R с
R = √OC²-OM² = √R²-x²
Так как S (x) = п r ², то S (x) = п (R²-x²). Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т.е., для всех х, удовлетворяющих условию –R ≤ x ≤ R. Применяя основную формулу для вычисления объёмов тел при a = –R, b = R, получаем:
R R R R R
V = ∫ п (R²-x²) dx = п R² ∫ dx - ∫ x²dx = п R²x | - пx³/3 | = 4/3 пR³.
-R -R -R -R -R
Теорема доказана




![Презентация по математике Первообразная Если f – непрерывная и неотрицательная на отрезке [a; b]функция , Если f – непрерывная и неотрицательная на отрезке [a; b]функция , а F – ее первообразная на](/img/thumbs/f889a852b20e99bd9ef72f778c257561-800x.jpg)