- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Парабола вокруг нас
Содержание
- 1. Презентация по математике Парабола вокруг нас
- 2. Нет ни одной области математики,как бы абстрактна
- 3. Гипотеза: квадратичная функция зародилась из практических запросов
- 4. Цель:изучить одну из кривых второго порядка(параболу)и сферы её применения.
- 5. Задачи: 1.Дать определение параболы.2. Изучить свойства параболы.3.
- 6. Объект исследования: Парабола в математике и жизни.
- 7. Актуальность работы заключается в том, что в
- 8. Аполлоний Пергский (Перге, 262 до н.э. —
- 9. Пара́бола (греч. παραβολή — приложение) —кривая, точки
- 10. Еще один способ построенияОказывается, что парабола –
- 11. Для того чтобы нарисовать параболу, потребуются линейка,
- 12. Слайд 12
- 13. Свойства параболы1. Парабола — кривая второго порядка.2.
- 14. Парабола имеет ось симметрии.
- 15. Применение параболы в физике, технике, баллистике.Можно привести
- 16. Примерами зависимостей квадратичной функции являются зависимости:Мощности электрического
- 17. Слайд 17
- 18. Баллистика (от греч. βάλλειν — бросать) —
- 19. Параболические траектории струй воды
- 20. Слайд 20
- 21. С точки зрения спортсменов: прыгунов в высоту
- 22. Слайд 22
- 23. Слайд 23
- 24. Параболоид вращения.Если вращать параболу вокруг ее оси
- 25. Параболоид вращения фокусирует пучок лучей, параллельный главной
- 26. Использование параболоидов в техникеТелескопы-рефлекторыПрожекторАвтомобильные фары
- 27. Солнечная зажигалкаОригинальный способ использования энергии Солнца. Солнечная
- 28. Слайд 28
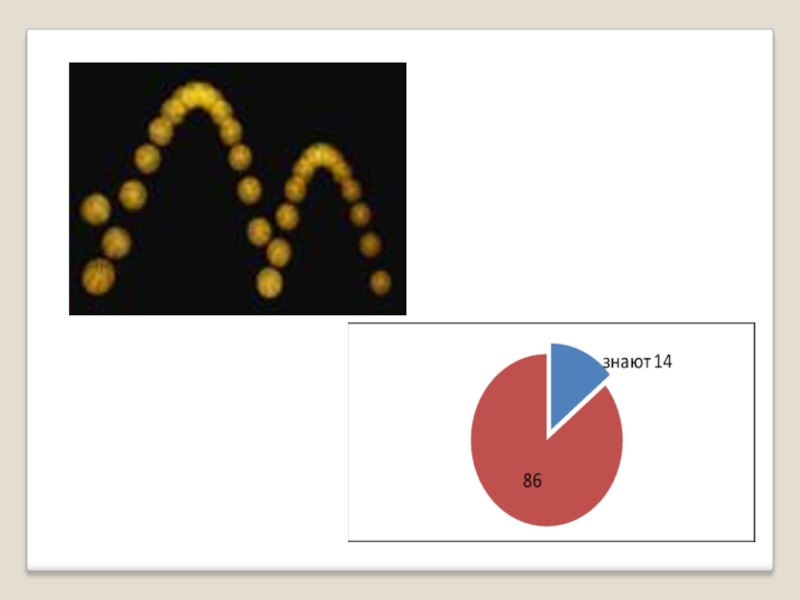
- 29. Траектории прыжков животных близки к параболе
- 30. Слайд 30
- 31. Слайд 31
- 32. Парабола находит широкое применение в мостостроении.
- 33. ВИСЯЧИЙ МОСТ ДИТ © 2014 Под
- 34. ЗаключениеПрирода в различных своих творениях, казалось бы,
- 35. Слайд 35
- 36. Слайд 36
- 37. Литература.Словарь юного математика.http://ru.wikipedia.org/wiki/Парабола http://ru.wikipedia.org/wiki/Параболоид«Физика-9», изд-во «Дрофа», Перышкин А.В.,М., 2018 г.Интернет ресурсы.Сайт ФИПИ
Нет ни одной области математики,как бы абстрактна она ни была,которая когда-нибудь не окажется применимойк явлениям действительного мираН.И. Лобачевский
Слайд 1Тема:Парабола вокруг нас.
Автор работы:Жалнировская Елена
9 А класс
Учитель:Жалнировская Татьяна Викторовна
Слайд 2
Нет ни одной области математики,
как бы абстрактна она ни была,
которая когда-нибудь
не окажется применимой
к явлениям действительного мира
Н.И. Лобачевский
к явлениям действительного мира
Н.И. Лобачевский
Слайд 3Гипотеза:
квадратичная функция зародилась из практических
запросов человечества, с ёе
помощью люди могут
управлять природой,
она проникла и в другие науки.
управлять природой,
она проникла и в другие науки.
Слайд 5Задачи:
1.Дать определение параболы.
2. Изучить свойства параболы.
3. Выяснить, почему параболу называют
коническим сечением.
4. Выявить области применения параболы
5. Показать межпредметные связи
(математики и физики)
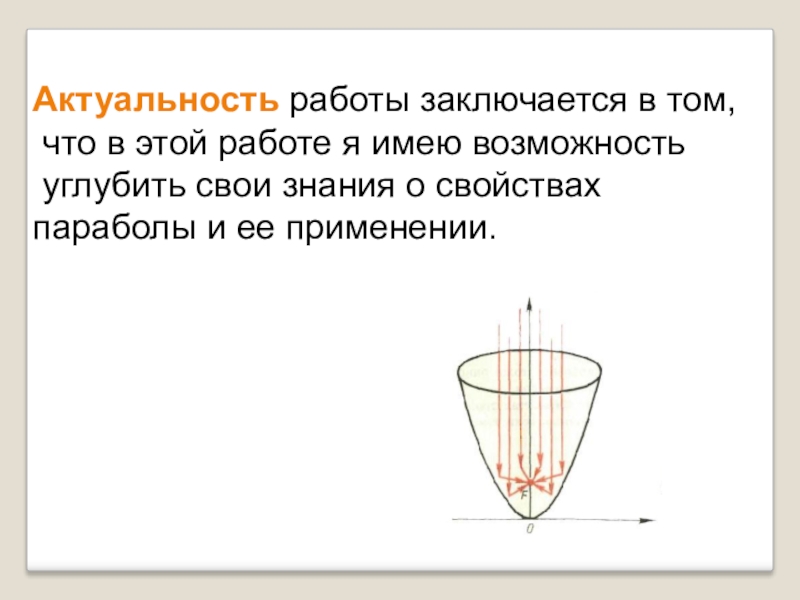
Слайд 7Актуальность работы заключается в том,
что в этой работе я имею
возможность
углубить свои знания о свойствах параболы и ее применении.
углубить свои знания о свойствах параболы и ее применении.
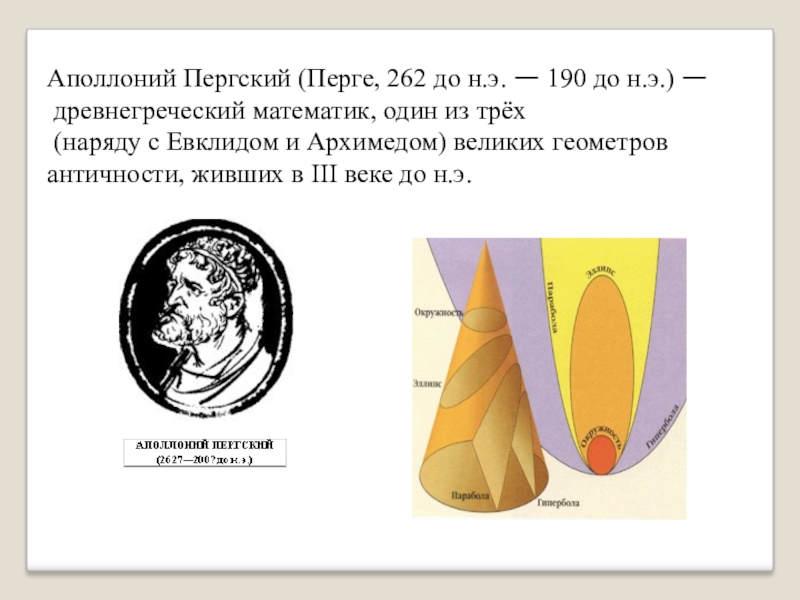
Слайд 8Аполлоний Пергский (Перге, 262 до н.э. — 190 до н.э.) —
древнегреческий математик, один из трёх
(наряду с Евклидом и Архимедом) великих геометров
античности, живших в III веке до н.э.
(наряду с Евклидом и Архимедом) великих геометров
античности, живших в III веке до н.э.
Слайд 9Пара́бола (греч. παραβολή — приложение) —кривая, точки которой одинаково удалены от
некоторой точки, называемой фокусом, и от некоторой прямой, называемой директрисой параболы.
Слайд 10Еще один способ построения
Оказывается, что парабола – график квадратичной функции –
обладает интересным свойством: есть такая точка и такая прямая, что каждая точка параболы одинаково удалена от этой точки и от этой прямой (точку называют фокусом параболы, а прямую – директрисой). Это свойство параболы было известно еще математикам античной Греции. Для графика функции у = х2 фокусом служит точка с координатами (0;0,25), а директрисой – прямая у = -0,25.
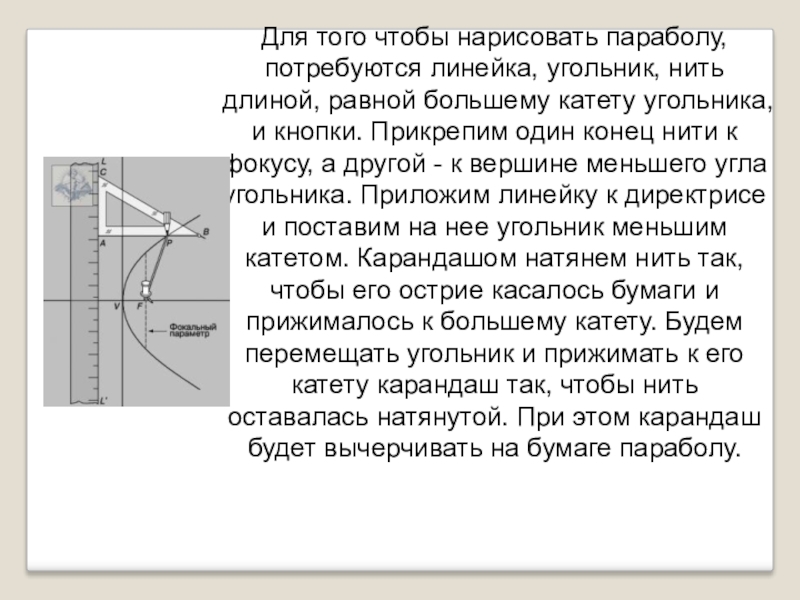
Слайд 11Для того чтобы нарисовать параболу, потребуются линейка, угольник, нить длиной, равной
большему катету угольника, и кнопки. Прикрепим один конец нити к фокусу, а другой - к вершине меньшего угла угольника. Приложим линейку к директрисе и поставим на нее угольник меньшим катетом. Карандашом натянем нить так, чтобы его острие касалось бумаги и прижималось к большему катету. Будем перемещать угольник и прижимать к его катету карандаш так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать на бумаге параболу.
Слайд 13Свойства параболы
1. Парабола — кривая второго порядка.
2. Она имеет ось симметрии.
Ось проходит через фокус и вершину перпендикулярно директрисе.
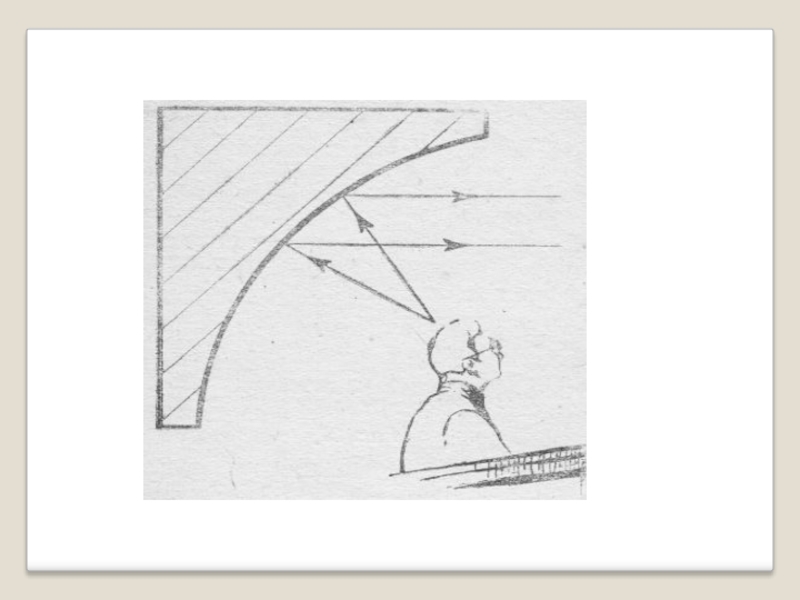
3.Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе.И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
4. Для параболы фокус находится в точке (0; 0.25).
5.Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
3.Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе.И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
4. Для параболы фокус находится в точке (0; 0.25).
5.Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
Слайд 15Применение параболы в физике, технике, баллистике.
Можно привести немало примеров применения квадратичной
функции, из которых главный известный из учебника физики — уравнение пути равноускоренного движения
Множество траекторий полёта в однородном гравитационном поле без сопротивления воздуха какого-либо объекта (мяча,артиллерийского снаряда) соответствует параболе.
Слайд 16Примерами зависимостей квадратичной функции являются зависимости:
Мощности электрического тока P=I2R
при постоянном
сопротивлении, угол поворота при равнопеременном движении ϕ=ω0t+εt2/2,
кинетической энергии E=mv2/2 и другие формулы, связывающие различные физические величины.
кинетической энергии E=mv2/2 и другие формулы, связывающие различные физические величины.
Слайд 18Баллистика (от греч. βάλλειν — бросать) — наука о движении тел,
брошенных в пространстве, основанная на математике и физике. Она занимается, главным образом, исследованием движения снарядов, выпущенных из огнестрельного оружия, ракетных снарядов и баллистических ракет.
Слайд 21С точки зрения спортсменов: прыгунов в высоту и длину,
метателей, футболистов
и др., - заслуживают внимания факты, вытекающие из
приведённых формул:
Как дальность l, так и высота h пропорциональны квадрату
начальной скорости снаряда (копья, молота и т.п.). Так, например,
если увеличить начальную скорость бросания молота в 1,5 раза,
то дальность его падения увеличится более чем в 2 раза (при одном
и том же угле вылета снаряда);
Дальность будет наибольшей (при определённой скорости v),
когда α=45º
Высота прыжка будет наибольшей (при определённой скорости v)
когда угол α будет близок к 90º. Следовательно, спортсмен,
прыгающий в высоту, должен отталкиваться в момент прыжка как
можно ближе к планке;
.
Слайд 24Параболоид вращения.
Если вращать параболу вокруг ее оси вращения то получится поверхность,
которую называют параболоидом вращения.
Если сильно размешать ложечкой воду в стакане, а потом вынуть ложечку, то поверхность воды примет форму такого параболоида.
Если сильно размешать ложечкой воду в стакане, а потом вынуть ложечку, то поверхность воды примет форму такого параболоида.
Слайд 25Параболоид вращения фокусирует пучок лучей, параллельный главной оси, в одну точку.
Часто
используется свойство параболоида вращения собирать пучок лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника.
На этом принципе основаны параболические антенны, телескопы-рефлекторы, прожекторы, автомобильные фары.
На этом принципе основаны параболические антенны, телескопы-рефлекторы, прожекторы, автомобильные фары.
Использование параболоидов в технике
Слайд 27Солнечная зажигалка
Оригинальный способ использования энергии Солнца. Солнечная зажигалка представляет собой параболическое
зеркало из нержавеющей стали, почти такое же, как то, которое используется для зажигания Олимпийского огня в Афинах.
Параболическое зеркало дает возможность собрать всю энергию в одной фокусной точке и зажечь огонь. Температура в этой точке может достигать 537-ми градусов по Цельсию. Такое устройство будет незаменимо в походе и в других полевых условиях.
Параболическое зеркало дает возможность собрать всю энергию в одной фокусной точке и зажечь огонь. Температура в этой точке может достигать 537-ми градусов по Цельсию. Такое устройство будет незаменимо в походе и в других полевых условиях.
Слайд 33ВИСЯЧИЙ МОСТ
ДИТ © 2014
Под действием собственного веса и веса
мостового пролёта тросы провисают и образуют дугу, близкую к параболе. Ненагруженный трос, подвешенный между двумя опорами, принимает форму т. н. «цепной линии», которая близка к параболе в почти горизонтальном участке. Если весом тросов можно пренебречь, а вес пролёта равномерно распределён по длине моста, тросы принимают форму параболы.
Слайд 34Заключение
Природа в различных своих творениях, казалось бы, очень
далеких друг от
друга, может использовать одни и те же
принципы.
И человек в своих творениях: живописи, скульптуре,
архитектуре…
Основополагающими принципами красоты при этом
являются пропорции и симметрия – то,
что содержит парабола.
Я считаю, что в своей работе доказала выдвинутую гипотезу.
принципы.
И человек в своих творениях: живописи, скульптуре,
архитектуре…
Основополагающими принципами красоты при этом
являются пропорции и симметрия – то,
что содержит парабола.
Я считаю, что в своей работе доказала выдвинутую гипотезу.
Слайд 37Литература.
Словарь юного математика.
http://ru.wikipedia.org/wiki/Парабола
http://ru.wikipedia.org/wiki/Параболоид
«Физика-9», изд-во «Дрофа», Перышкин А.В.,М., 2018 г.
Интернет ресурсы.
Сайт
ФИПИ