Автор разработки:
Дергачёва Елена Валентиновна
учитель математики
МАОУ г. Ростова-на-Дону «Школа № 87 имени Героя Советского Союза
Щербакова Николая Митрофановича»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Обратные тригонометрические функции. 11 класс
Содержание
- 1. Презентация по математике Обратные тригонометрические функции. 11 класс
- 2. Мы изучаем группу трансцендентных функций, в которую кроме тригонометрических входят показательная и логарифмическая функции.
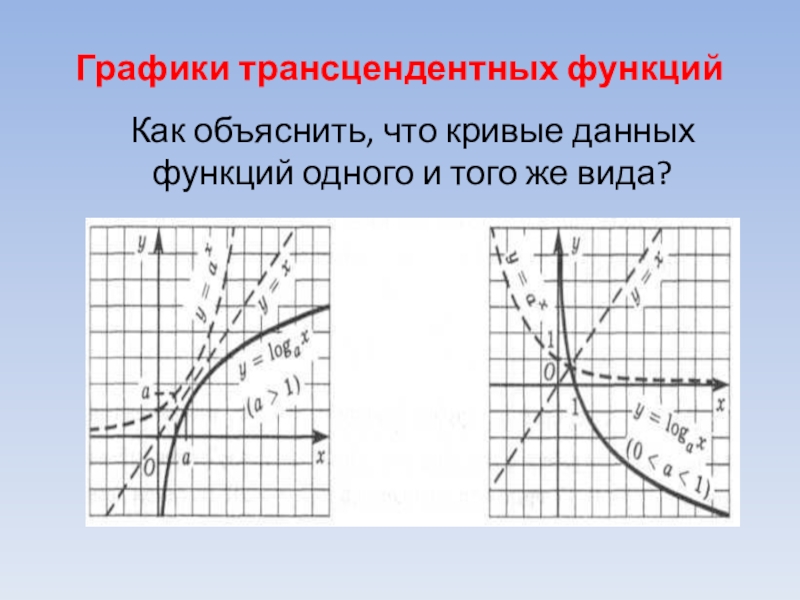
- 3. Графики трансцендентных функций Как объяснить, что кривые данных функций одного и того же вида?
- 4. Свойства взаимно обратных функцийГрафики взаимно обратных функций
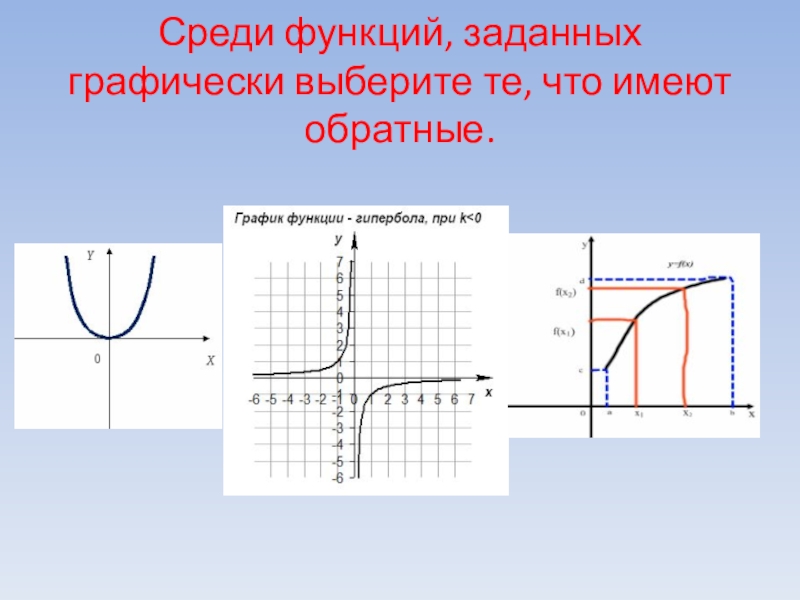
- 5. Среди функций, заданных графически выберите те, что имеют обратные.
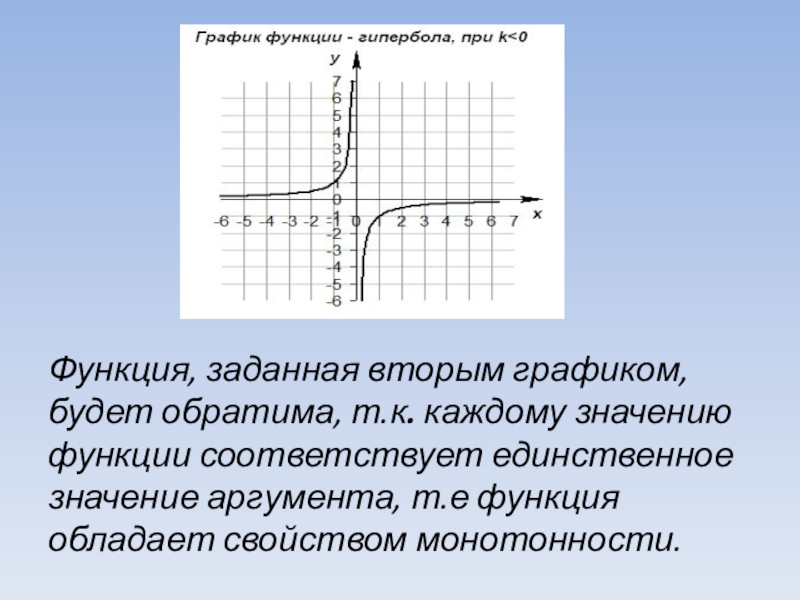
- 6. Функция, заданная вторым графиком, будет обратима, т.к. каждому
- 7. Какие знания мы использовали, устанавливая обратимость функций?При
- 8. Обратные тригонометрические функции, их графики.
- 9. Обратные тригонометрические функции
- 10. Слайд 10
- 11. Область определения функции — множество R всех
- 12. Слайд 12
- 13. у = arcsinxСодержаниех1)Область определения: отрезок [-1; 1];
- 14. Область определения функции — множество R всех
- 15. Свойства функции y = arccos x .cos(arccosx)
- 16. Графики обратных тригонометрических функций Графики обратных тригонометрических
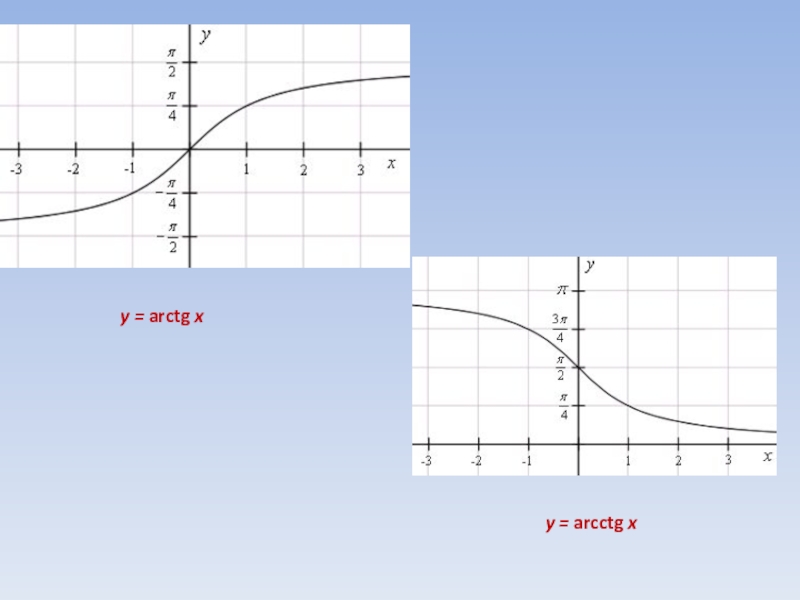
- 17. y = arctg xy = arcctg x
- 18. у=arctgxСодержание1)Область определения: R – множество действительных чисел
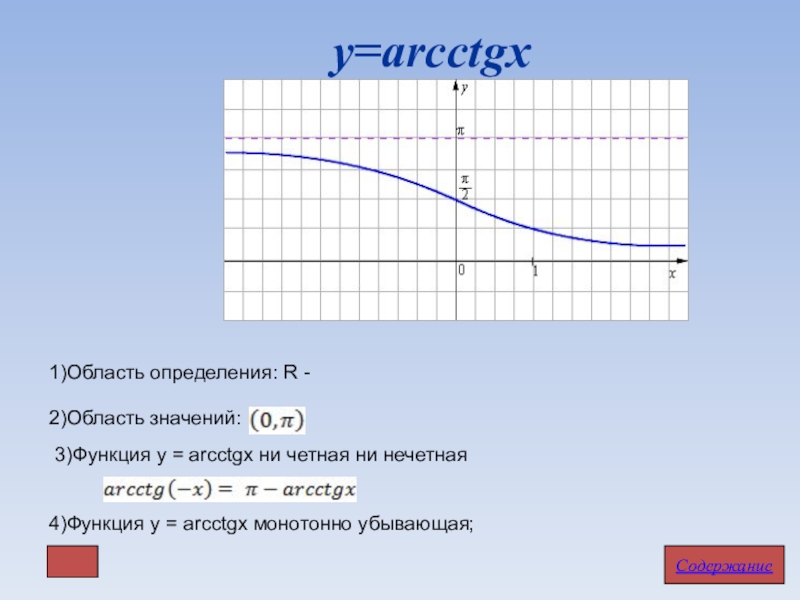
- 19. у=arcctgxСодержание1)Область определения: R - 2)Область значений:
- 20. Работаем устноСодержаниеarcsin(-x) = - arcsinxarccos(-x) = - arccosx
- 21. Решаем по учебнику :№758 (1,3,5)№759 (1,3,5)№760 (1,3)№761 (1)№762(1,3)
- 22. Подведение итогов. На уроке познакомились с
- 23. Спасибо за урок !!!!!!
Слайд 1Методическая разработка урока алгебры в 11 классе по теме «Обратные тригонометрические функции,
Слайд 2Мы изучаем группу трансцендентных функций, в которую кроме тригонометрических входят показательная
Слайд 3
Графики трансцендентных функций
Как объяснить, что кривые данных функций одного и того же
Слайд 4Свойства взаимно обратных функций
Графики взаимно обратных функций обладают свойством симметрии относительно
Слайд 6
Функция, заданная вторым графиком, будет обратима, т.к. каждому значению функции соответствует единственное
Слайд 7Какие знания мы использовали, устанавливая обратимость функций?
При выполнении данного задания мы
Слайд 11Область определения функции — множество R всех действительных чисел.
Множество значений функции
Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2π:
Функция у = sinx
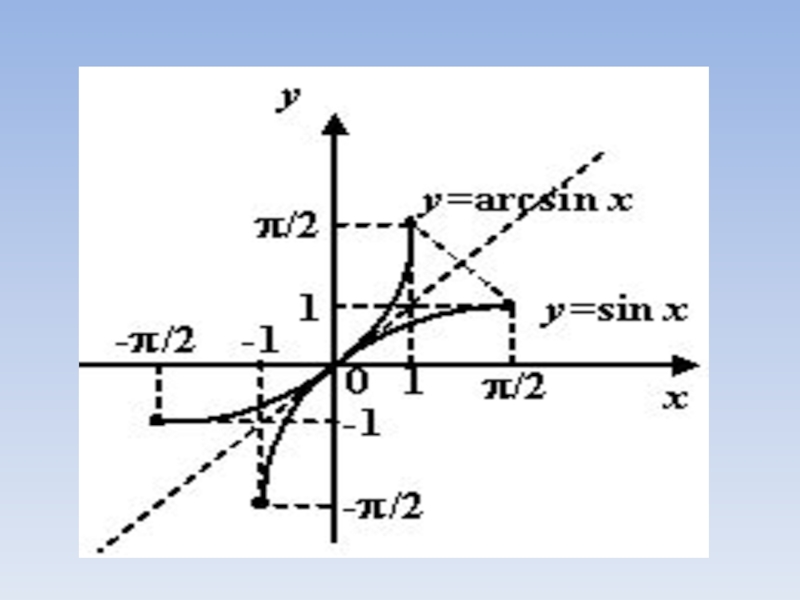
Слайд 13у = arcsinx
Содержание
х
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
;
3)Функция у = arcsin x нечетная:
arcsin (-x) = - arcsin x;
4)Функция у = arcsin x монотонно возрастающая;
Слайд 14Область определения функции — множество R всех действительных чисел.
Множество значений функции
Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2π:
Функция у = cosx
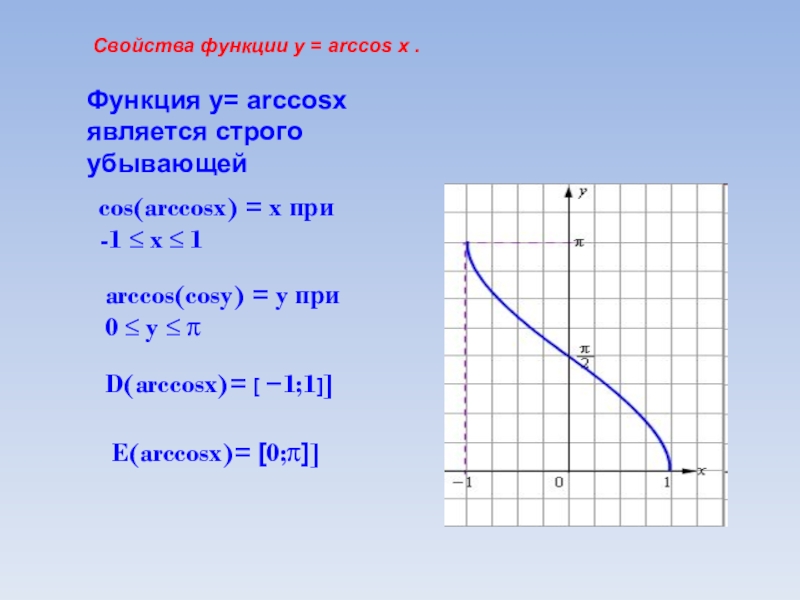
Слайд 15Свойства функции y = arccos x .
cos(arccosx) = x при
-1
Функция y= arccosx является строго убывающей
arccos(cosy) = y при
0 ≤ y ≤ π
D(arccosx)= [ −1;1]]
E(arccosx)= [0;π]]
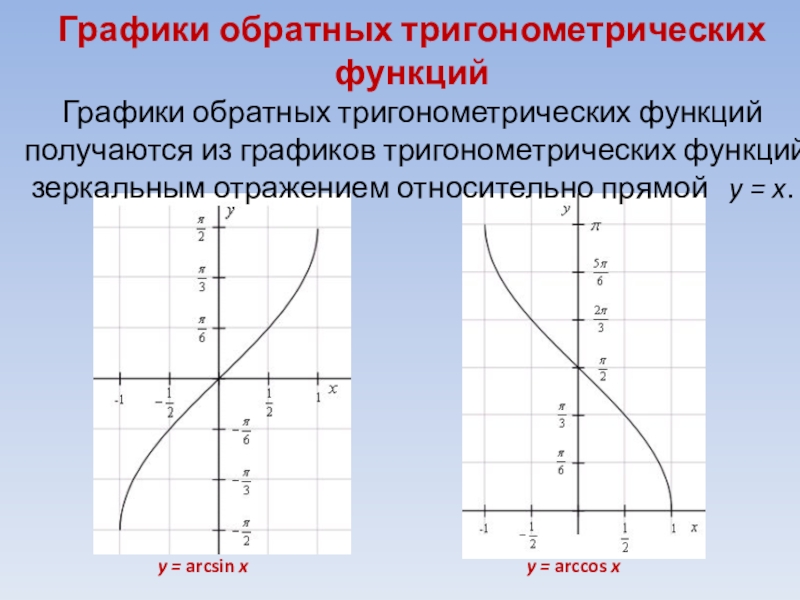
Слайд 16Графики обратных тригонометрических функций Графики обратных тригонометрических функций получаются из графиков тригонометрических
y = arcsin x
y = arccos x
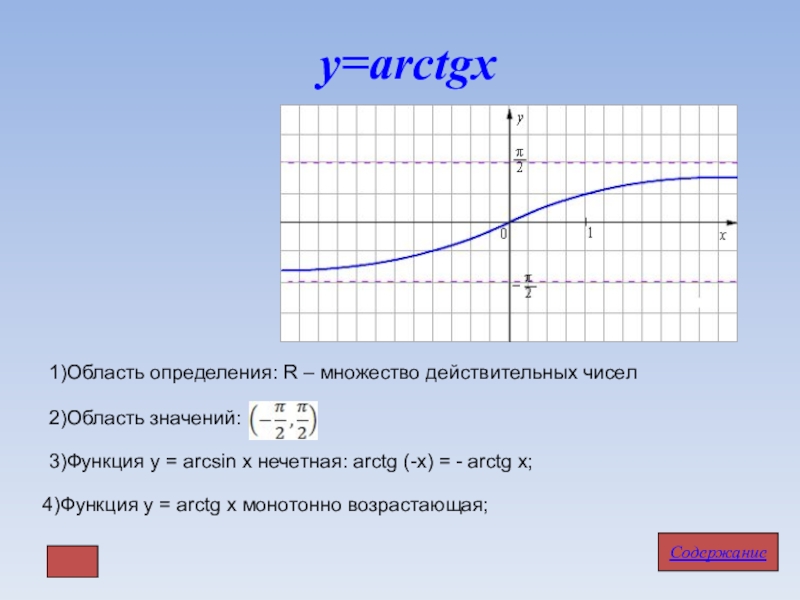
Слайд 18у=arctgx
Содержание
1)Область определения: R – множество действительных чисел
2)Область значений:
3)Функция
4)Функция у = arctg x монотонно возрастающая;
Слайд 19у=arcctgx
Содержание
1)Область определения: R -
2)Область значений:
4)Функция у = arcсtgx
3)Функция у = arcctgх ни четная ни нечетная
Слайд 22Подведение итогов.
На уроке познакомились с обратными тригонометрическими функциями, их графиками
Домашнее задание :
П 43; №758-762 (2,4)






![Презентация по математике Обратные тригонометрические функции. 11 класс Область определения функции — множество R всех действительных чисел.Множество значений функции Область определения функции — множество R всех действительных чисел.Множество значений функции — отрезок [-1; 1], т.е. синус](/img/thumbs/ee9bddd5d3beb74c99f6fdd3d2fed36a-800x.jpg)
![Презентация по математике Обратные тригонометрические функции. 11 класс у = arcsinxСодержаниех1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок ; у = arcsinxСодержаниех1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок ; 3)Функция у = arcsin x нечетная:](/img/thumbs/a53a3fd3b2101d803909b621d8bc74d9-800x.jpg)
![Презентация по математике Обратные тригонометрические функции. 11 класс Область определения функции — множество R всех действительных чисел.Множество значений функции Область определения функции — множество R всех действительных чисел.Множество значений функции — отрезок [-1; 1], т.е. косинус](/img/thumbs/95ea7c299b7002b1a9d0d96176b456de-800x.jpg)